包含Smarandache对偶函数的方程的正整数解

陈 斌

（渭南师范学院 数学系，陕西 渭南 714000）

包含Smarandache对偶函数的方程的正整数解

陈 斌

（渭南师范学院 数学系，陕西 渭南 714000）

Smarandache对偶函数；Ω函数；正整数解

1 引言及结论

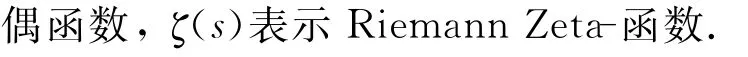
现设Ω（n）表示正整数n的所有素因子的个数（按重数计算），即若n＝pα11pα22…pαkk为正整数n的标准分解式，则Ω（n）＝α1＋α2＋…＋αk.考虑函数方程

张文鹏教授建议笔者研究方程（1）的可解性，本研究得到了这个方程的所有正整数解.即证明了如下定理：

定理 方程（1）所有偶数解为n＝24·330、n＝26·312、n＝8p7、n＝16p5、n＝64p4、n＝2pq，其中p、q≥5为奇素数；所有奇数解为n＝p、n＝pαq，其中α≥1，p、q为奇素数.

2 定理的证明

显然，由S＊（n）和Ω（n）的定义知，n＝1不是方程（1）的解，下面假设n＞1.

Ⅰ.若n为偶数，分以下几种情况讨论：

［1］ SMARANDACHE F.Only Problems，Not Solutions［M］.Chicageo：Xiquan Publishing House，1993.

［2］ 潘承洞，潘承彪.初等数论［M］.北京：北京大学出版社，1992.

［3］ 易媛，亢小玉.Smarandache函数问题研究［M］.西安：西北大学出版社，2006.

［4］ 张文鹏.关于F.Smarandache函数的两个问题［J］.西北大学学报：自然科学版，2008，38（2）：173－176.

［5］ 徐哲峰.Smarandache函数的值分布性质［J］.数学学报，2006，49（5）：1009－1012.

［6］ 李梵蓓.一个与Smarandache函数有关的函数方程及其正整数解［J］.西北大学学报：自然科学版，2008，38（6）：892－893.

［7］ SANDOR J.On certain generalizations of the Smarandache function［J］.Notes Number Theory and Discrete Mathematics，1999，5（2）：41－51.

［8］ SANDOR J.On a dual of the pseudo Smarandache function［J］.Smarandache Notions Journal，2002，13：18－23.

［9］ 张文鹏.初等数论［M］.西安：陕西师范大学出版社，2007.

［10］ APOSTOL T M.Introduction to Analytic Number Theory［M］.New York：Spring－Verlag，1976.

［11］ LOU Y B.On the pseudo Smarandache function［J］.Scientia Magna，2007，3（4）：48－50.

［12］ ZHENG Y N.On the pseudo Smarandache function and its two conjectures［J］.Scientia Magna，2007，3（4）：51－53.

［13］ 张爱玲.关于伪Smarandache函数的一个方程及其正整数解［J］.西北大学学报：自然科学版，2008，38（4）：535－536.

［14］ 王妤.一个包含Smarandache LCM对偶函数的方程［J］.黑龙江大学自然科学学报，2008，25（5）：23－27.

Positive integer solutions of an equation involving Smarandache dual function

CHENBin
（Department of Mathematics，Weinan Teachers University，Weinan 714000，Shaanxi Province，China）

By using the elementary number theory and combinational methods，the positive integer solutions of a function equation involving both of the Smarandache dual function and theΩfunction is studied.All the exact positive integer solutions are given for the equation，and it is proved that the evennsatisfy the equation only ifn＝24·330，n＝26·312，n＝8p7，n＝16p5，n＝64p4，n＝2pq，wherep，q≥5are both odd primes，and the oddnsatisfy the equation only ifn＝p，n＝pαq，wherep，qare both odd primes，α≥1.

Smarandache dual function；Ωfunction；positive integer solutions

O156.4

A

1671－1114（2012）03－0006－03

2012－12－10

国家自然科学基金资助项目（11071194）；陕西省科技厅自然科学基金资助项目（2012JM1021）；陕西省教育厅自然科学科研计划资助项目（12JK0880）；陕西省军民融合研究院2011年基金资助项目（11JMR10）；渭南师范学院科研基金资助项目（12YKS024）；信息安全国家重点实验室（中国科学院软件研究所）资助项目100190（2011NO：01－01－2）

陈 斌（1979—），男，讲师，主要从事数论方面的研究.

（责任编校 马新光）