旋转搅拌中流体液面的数学解

刘 旭，李宝毅

（天津师范大学 数学科学学院，天津 300387）

旋转搅拌中流体液面的数学解

刘 旭，李宝毅

（天津师范大学 数学科学学院，天津 300387）

利用数学分析的知识研究以下问题：一底面半径为R的圆柱形搅拌机内盛有牛顿流体，静止时流体的深度h足够大，且流体不会外溢.在位于对称轴上的半径为r的扇叶搅拌下，对称轴附近的流体绕着它以恒定角速度ω匀速转动，考虑此时液面的形状是怎样的.本研究给出了这个问题的精确解.

旋转搅拌；精确解；牛顿流体

数学分析的发展滥觞于微积分，并扩展到函数的连续性、可微性及可积性等各种特性.这些特性有助于人们发现及研究自然界的规律，微积分理论的诞生离不开物理学、天文学、几何学等领域的发展，微积分理论从其产生之日起便显示出可观的应用活力，所以在数学分析的研究中，可以强化微积分与相邻学科间的联系，强调应用背景，充实理论的应用性内容.目前此研究领域比较活跃，国内外不断涌现出高水平的研究成果，例如文献［1］通过力学分析，研究了绕中心轴等角速度旋转圆柱体容器内的液体平衡问题，给出了自由液面方程；随后，证明了旋转抛物体的体积为同底同高圆柱体体积的一半；其次，在柱坐标系下，给出了旋转抛物线与圆柱体的轴线和母线，以及原液面围成的2部分投影面积之间的数量关系.文献［2］研究了失重状态下圆环形容器内稳态旋转液体的液面形状，在确定了液面极值点的位置后，导出了液面形状的积分计算公式，分析了液面破裂时的临界转速，并求得了液面位置与液体体积之间的关系式.文献［3］的例2.2应用牛顿定律得到结论：一水桶内的水随水桶一起绕其自身轴以角速度ω匀速转动，所得水面形状为旋转抛物面.本研究将利用数学分析的知识及牛顿定律，结合Mathematica7.0软件，就旋转搅拌问题展开讨论，并通过考察粘滞定律及流体的速度梯度，在更复杂的模型中讨论了该问题.

如图1所示，一个半径为R的圆柱形搅拌机内盛有牛顿流体（即满足粘滞定律的流体），静止时流体的深度h足够大，且流体不会外溢.在位于对称轴上的半径为r的扇叶搅拌下，对称轴附近的流体绕着它以恒定角速度ω匀速转动，r≤1≤R，考虑此时液面的形状是怎样的.

图1 旋转搅拌机示意图Fig.1 Schema of gyratory shaker

选择搅拌机的外壳为参照物，y轴为转动轴，水平轴x如图1所示，z轴垂直于纸面指向纸外.在桶右侧选取位于xOy平面上、到转动轴线的距离为x的A点处的液面上的质量元dM.易知此质量元做匀速圆周运动，受到液面的支持力N和重力G＝gdM，二者的合力提供水平方向的向心力F＝ω2（x）xdM，当液面稳定时，N应与液面在A点的切线垂直.

设液面在xOy右半平面内的截线为y＝y（x），则有

任意给定一种情况，如当g＝9.8，h＝5，r＝0.01，R＝2，ω＝3时，y（x）的图像如图2所示，此时液面的形状如图3所示.

下面再给出一种更为有趣的情况，当g＝9.8，h＝8，r＝1，R＝2，ω＝3时，y（x）的图像如图4所示，此时液面的形状如图5所示.

本研究所涉及的问题看似简单，但计算的空间复杂度令人头痛，已经到了不得不放弃手工运算的地步.由此可见，计算机代数的方法十分有效，特别是在基础数学领域，可以利用软件的符号计算功能，在短时间内完成大量的理论推导，使得数学工作者可以像做物理实验一样，快速对理论的细节做出预测.计算机代数（Computer Algebra）在很多时候又被广义地理解为“符号计算”（Symbolic Computation），成为与所谓“数值计算”相对的概念.“符号”的运算在这里代替了“数”的运算.这是一种智能化的计算，处理的是符号.符号可以代表整数、有理数、实数和复数，也可以代表多项式、函数，还可以代表数学结构如集合、群、环、代数等.利用计算机代数，可以完成许多不可思议的任务，如可对方程组进行精确求解，对多项式进行因式分解，对复杂代数表达式进行化简，对函数进行符号积分（求出原函数），对微分方程求出解析解等.

图2 当g＝9.8，h＝5，r＝0.01，R＝2，ω＝3时y（x）的图像Fig.2 Picture of y（x）when g＝9.8，h＝5，r＝0.01，R＝2，ω＝3

图3 当g＝9.8，h＝5，r＝0.01，R＝2，ω＝3时的液面形状Fig.3 Shape of liquid level when g＝9.8，h＝5，r＝0.01，R＝2，ω＝3

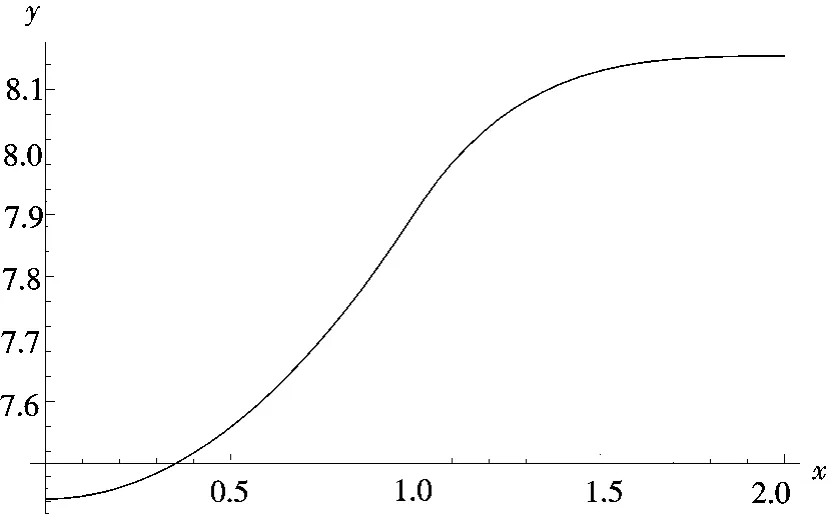
图4 当g＝9.8，h＝8，r＝1，R＝2，ω＝3时y（x）的图像Fig.4 Picture of y（x）when g＝9.8，h＝8，r＝1，R＝2，ω＝3

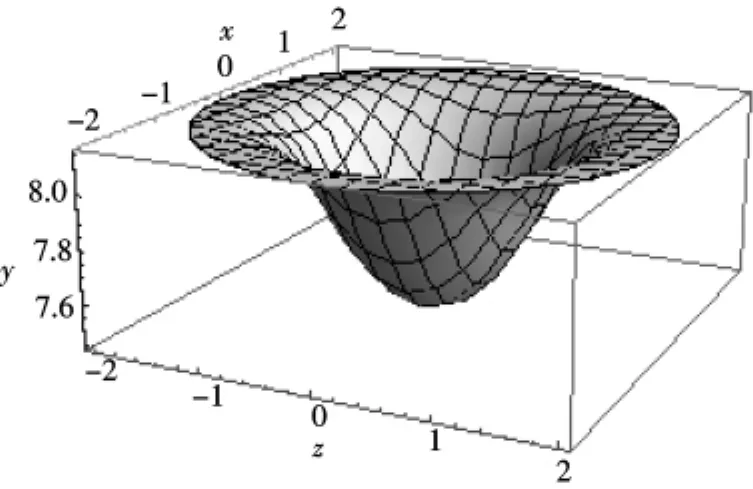
图5 当g＝9.8，h＝8，r＝1，R＝2，ω＝3时的液面形状Fig.5 Shape of liquid level when g＝9.8，h＝8，r＝1，R＝2，ω＝3

［1］ 叶春生，葛均建，崔世平，等.水静力学中旋转抛物体问题的进一步分析［J］.河南科学，2009，27（5）：571－574.

［2］ 周叮.失重状态下圆环形容器内旋转液体的液面形状分析［J］.强度与环境，1994（4）：40－44.

［3］ 田清钧.基础力学［M］.北京：国防工业出版社，2001.

［4］ WILFRED K.Advanced Calculus［M］.北京：电子工业出版社，2004.

［5］ JIRÍG，JAROSLAV T.Discovering Mathematics：A Problem－Solving Approach to Mathematical Analysis with Mathematica and Maple［M］.New York：Springer Publishing，2011.

Exact solution of liquid level with rotary stirring

LIUXu，LIBao－yi
（College of Mathematical Science，Tianjin Normal University，Tianjin 300387，China）

Mathematical analysis is used to study the issue as follow：A cylindrical mixer with bottom radiusRcontains Newtonian fluid with the depthhwhich is large enough，and the fluid does not spill.At the symmetry axis the flabellum’s radius isr，the fluid near the symmetry axis performs a rotation at a constant angular velocityωaround the symmetry axis.Exact solution of the shape of the liquid level is obtained.

rotary stirring；exact solution；Newtonian fluid

O175.1

A

1671－1114（2012）03－0024－04

2011－10－14

刘 旭（1987—），男，硕士研究生.

李宝毅（1963—），男，教授，主要从事常微分方程及其应用方面的研究.

（责任编校 马新光）