含Hilbert核的奇异积分方程组

张军好，胡军浩

(中南民族大学 数学与统计学学院，武汉 430074)

含Hilbert核的奇异积分方程及其解法在文[1]中有详细的讨论.本文在文[1]的基础之上讨论了含Hilbert核的奇异积分方程组.利用复变函数的方法将其转化为周期Riemann边值组问题,最后利用文[2]的方法给出了该问题的可解性条件,并得出了其解的一般表达式.

1 预备知识

据文[2]可知周期Riemann边值组问题：

Φ+(t0)=G(t0)Φ-(t0)+g(t0),t0∈L0.

(1)

其中：

Φ(z)=(Φ1(z),Φ2(z),…,Φn(z))T,G(t0)=[Gij(t0)]n×n,g(t0)=(g1(t0),g2(t0),…，gn(t0))T且G(t0),g(t0)均以απ为周期同时属于H类，G(t0)的行列式detG(t0)≠0,t0∈L0.

据文[2]的结果可知(1)式解存在的充分必要条件为g(t)满足：

(2)

此时其解的一般表达式为：

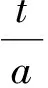
(3)

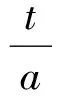
Φ(+∞i)=-Φ(-∞i).

(4)

令z=±∞i分别代人(3)式中，则(1)式满足(4)式的解所需的附加条件变为：

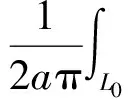
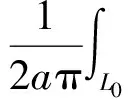
即:

G∞p(-i)+p(+i) .

(5)

其中G∞=[X(+∞i)]-1·X(-∞i),E为n阶单位矩阵.

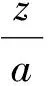
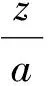
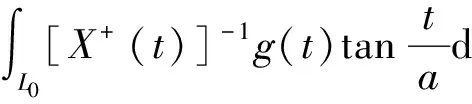
2 含Hilbert核的奇异积分方程组及其求解

为了简单起见，设L为一条封闭的光滑曲线，而且将它沿实轴方向平移aπ(a>0)单位时，得到的合同曲线与L不相交.求解含Hilbert核的奇异积分方程组：

fi(t0),t0∈L,i=1,2，…，n.

(6)

其中Aij(t0),Bij(t0),fi(t0)为已知的在L上满足H条件的函数，ρi(t)为未知函数.

引进向量函数ρ(t)=(ρ1(t)，ρ2(t),…，ρn(t))T,f(t)=(f1(t)，f2(t),…，fn(t))T及n阶方阵A(t0)=[Aij(t0)]n×n,B(t0)=[Bij(t0)]n×n,则方程组(6)可写为：

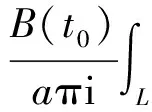
(7)

为了求解上述方程组(6)及(7)式，据文[1]，类似于求解一般奇异积分方程的方法令：

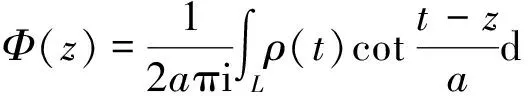
(8)

ρ(t0)=Φ+(t0)-Φ-(t0).

(9)

故(7)式变为：

Φ+(t0)=G(t0)Φ-(t0)+g(t0),t0∈L.

(10)

其中G(t0)=(A+B)-1·(A-B)=S-1·T，g(t0)=(A+B)-1·f(t0)=S-1f(t0).

反过来,类似文[1]中对带Hilbert核的奇异积分方程的讨论可知，如果Φ(z)是以aπ为周期的分区全纯函数，以L为跳跃曲线，同时满足边值条件(10)式及附加条件(4)式，则(9)式所确定的ρ(t0)必为(7)式问题的解.综合有以下定理1.

定理1 含Hilbert核的奇异积分方程组(6)式等价于周期Riemann边值组问题(10)式及附加条件(4)式，其解以(9)式给出.

下面利用文[2]和[6]中的方法求解问题(6).

仍设κ1≥κ2≥…≥κm≥0≥κm+1≥…≥κn.由于当(2)式成立时，(9)式有一般解为：

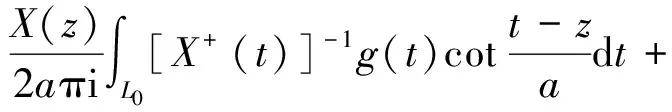
此时附加条件Φ(+∞i)=-Φ(-∞i)变为:

p(i)+G∞·p(-i).

(11)

故由(9)式可得方程组(7)式的一般解为：

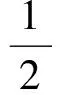
{[X+(t0)]-1+[X-(t0)]-1}g(t0)+

(12)

其中p(ξ)须满足附加条件(11)式，特别地，当κ1<0时须满足(5)式.

则解(12)式变为：

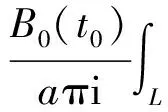
(13)

此时可解条件变为：

(14)

其中q(ξ)=(q-κ1+2,…，q-κn+n)T.

附加条件变为：

(15)

特别地当κ1<0时,据文[7]有：

(16)

故得以下定理2.

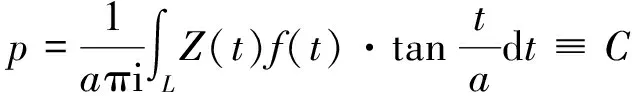
[1]路见可.解析函数边值问题[M].上海：上海科学技术出版社，1987.

[2]张军好，胡军浩.周期Riemann边值组问题[J].中南民族大学学报：自然科学版，2010,29(4)：112-114.

[3]Bekya H П.奇异积分方程组及某些边值问题[M].上海：上海科学技术出版社，1963.

[4]路见可.解析函数边值问题中的一些想法[J].武汉大学学报：自然科学版，1962(1)：1-8.

[5]路见可，钟寿国，刘士强.复变函数[M].武汉：武汉大学出版社，1992.

[6]Lu Jianke.Complex variable methods in plane elasticity[M].Singapore: World Scientific,1995.

[7]路见可.关于Hilbert核的奇异积分方程[J].数学进展，1965,2(8):161-167.