SEC-DED海明校验码算法研究及其FPGA实现
何秉姣,刘 科
(中南民族大学 计算机科学学院,武汉 430074)
数字系统中的数据在读写操作中出现差错是不可避免的,采用数据校验码检查和纠错可以减少或避免差错.海明校验码是目前被广泛采用的一种很有效的校验方法,它是能查错、纠错的线性分组码[1,2].通用的半导体存储器主要采用SEC-DED海明校验码(简称SEC-DED校验码或SEC-DED码)进行数据校验,它具有发现2位错和纠正一位错的能力.用硬件实现SEC-DED码的速度更快、更可靠.
FPGA深亚米微米的制造工艺实现了芯片集成成千上万的查找表和触发器,它的容量足以满足普通系统开发的需要.另外FPGA具有设计周期短、调试方便、开发费用低、风险小、与CMOS、TTL电平兼容等特点,使得FPGA芯片在工程项目中得到广泛应用[3-5].
1 SEC-DED海明校验码算法研究
海明码的基本算法就是将有效数据按某种规律分成若干组.每组安排1个校验位进行奇偶校验.在1个数据组中加入几个校验位,增大数据代码间的码距,当某一位发生变化时会引起校验结果发生变化,不同数位上的错误会得出不同的校验结果,从而实现查错和纠错.
1.1 SEC-DED校验位位数的确定
设有效数据为n位,校验位为k位,分成k组做奇偶校验,这样能产生k位检错信息.k位信息就构成1个指误字G=GkGk-1…G2G1,可构成2k种状态,其中1种状态表示无误,余下2k-1种表示或1位有效数据位出错,或校验位中有1位出错.因此共有1+k+n种情况,所以要对1位错的所有结果进行正确表示,则k和n满足如下关系:1+k+n≤2k.
故当有效数据位数有8位时,校验位至少要4位,一般表示为(12,8)形式.(12,8)海明码最多可以表示16种状态,而单个位出错情况最多只有12种可能,加上无错的情况,一共13种.所以16种状态表示13种情况足够.这种码能检查并纠正1位错,或者能发现2位出错,称为单纠错码(SEC).SEC-DED海明校验码在SEC基础上增加1位校验码,即(13,5),n=8,k=5,能发现2位出错,并能检查和纠正1位错.
1.2 SEC-DED校验位值确定
若海明码的最高位为m,最低位为1,即H=HmHm-1…H2H1.海明码编码规则:位号数(1,2,3,…,m)为2的幂次方值的那些有效位(即1,2,4,…,2k-1位),作为奇偶校验位,并记作P1,P2,P3,…,Pk,余下各位则为有效数据位.校验位与有效数据位之和为m,可令有效数据M=Mm-kMm-k-1…M2M1.SEC(12,8)相应的海明码如表1所示.

表1 SEC(12,8)海明码
其中每1位Hi都被P1,P2,P3,…,Pk中的1位或若干位所校验.例如H6被P2和P4所校验,H9被P1和P8所校验.其规律:第i位由校验位位号之和等于i的那些校验位所校验.由此可得SEC海明码每位所占的校验位,如表2所示.

表2 SEC海明码每位所占的校验位
从表2可看到某一位海明码是由哪几位校验位所校验.反过来,每个校验位,校验着它以后的一些确定位置上的海明码,包括它本身.例如P1校验着海明码中的第1、3、5、7、9、11位.归纳起来,SEC每个校验位所校验的数位如表3所示.

表3 SEC中每个校验位所校验的数位
综合起来,可以得到指误字与出错情况的对应关系,如表4所示.

表4 SEC码指误字与出错情况对应关系
表4对12位海明码字分成了4组,若某组中G的1位发生错误,那么该组对应的那些位就发生变化,可以根据该组对应的指误位Gi的值是否为1,来判断奇偶性是否发生了变化,从而确定该组中是否发生了1位错误.从表4可以看出,每一个有效数据位至少参与两组奇偶校验位的生成,例如M3与第2组(P2)和第3组(P3)有关.
分组后,就可对每组采用相应的奇(偶)校验,得到相应的校验位.SEC海明码采用偶校验,校验位与有效数据位之间关系如下:
(1)
SEC海明码中,如果2个数据有1位不同,那么由于该位至少要参与2组校验位的生成,因而至少引起2个校验位的不同,再加上数据位本身1位的不同,所以码距为3.码距为3的海明码具有发现2位出错,或者具有对单个错误定位和纠错的功能.要想同时具有发现2位错误和纠正1位错的能力,码距需扩大到4,在SEC基础上,增加1位校验位P5,将P5排列在码字的最前面,即H=P5M8M7M6M5P4M4M3M2P3M1P2P1,并使得有效数据中的每1位都参与3个校验位的生成,从方程组(1)可看出,除了M4和M7外,其余都只参与了2个校验位的生成.因此P5可按下式求出:
P5=M8⊕M6⊕M5⊕M3⊕M2⊕M1.
(2)
求SEC-DED校验位值的公式由方程组(1)和(2)式组合求得:
(3)
这样当任意1个数据位发生错误,必然引起3个校验位发生变化,所以码距为4.
1.3 SEC-DED校验方程及出错定位与纠正
引入P5后,指误字G也增加1位,即G=G5G4G3G2G1,根据表4得到方程组(4),可求出G中各位的值.
(4)
根据G5G4G3G2G1的取值情况,就可按照如下规则发现2位错并纠正1位错.
(1) 当G5,G4,G3,G2,G1全为0时,表明无错.
(2) 当G5,G4,G3,G2,G1中仅1位不为0 时,表明由G指定位置上的那个Pi出错,或是在Hi中有3位同时出错,但后面这种情况可能性非常小,所以一般认为发生了前一种情况.
(3) 当G5,G4,G3,G2,G1中有2位不为0时,表明Hi中有2位同时出错,此时只能发现这种错误,但无法确定哪两位出错.
(4) 当G5,G4,G3,G2,G1中有3位不为0时,表明由1个Mi发生了错误,或是3个Pi同时错误,但后面这种情况可能性非常小,所以一般认为发生了前一种情况.此时,出错位置由G4G3G2G1的数值确定.
(5) 当G5,G4,G3,G2,G1中有4位或5位不为0时,表明出错情况严重,系统可能出现故障,应检查系统硬件的正确性.
2 SEC-DED海明校验码FPGA的实现
基于FPGA的SEC-DED海明校验码实现系统包括编码器和译码器两部分,如图1所示.

图1 SEC-DED海明校验码编译码框图
结合案例解释编码器和译码器的功能.在控制电路的控制下,发送端发送8位M=11001011,据方程组(3)由编码器生成P=10110,则H=1110001011110,存入存储器.当读出该数据时,据方程组(4)由译码器生成G.如果无错,G=00000,否则有错.如读出数据H′=1100001011110,其中M′=10001011,P′=10110,则G=01011,由此定位第11位出错,并由纠正电路将其取反即可纠正.其它错误予以报警处理.下面给出基于Multisim 11.0的SEC-DED海明校验码编码器译码器的FPGA实现[6-9].
2.1 SEC-DED海明校验码编码器设计
基于方程组(3)在Multisim 11.0的平台下设计SEC-DED海明校验码编码电路.电路主要由5个多输入的异或门组成,将8位有效数据M,按方程组(3)连接构成.8位有效数据M,经过编码得到5位校验码P,合成海明码H存入存储器,其实验结果如图2 所示.
图2给出了字发生器模拟发送4组M,经过编码得到4组P,用逻辑分析仪仿真时序关系.当M=11001011时,逻辑分析仪的140 ms后1个周期内P=10110,当M=01101100时,逻辑分析仪中150 ms后的P=00010.与方程组(3)所求值相符.

图2 SEC-DED编码时序仿真
2.2 SEC-DED海明校验码译码器设计
(1) 指误码G产生电路.SEC-DED海明校验码译码器分指误码电路和纠错电路.基于方程组(4)在Multisim 11.0的平台下设计SEC-DED海明校验码译码电路.电路同样由5个多输入异或门组成,但结构与编码器电路不同.由字发生器XWG1模拟从存储器读出13位SEC-DED海明码H,经过译码得到5位指误码G,其实验结果如图3所示.

图3 SEC-DED译码时序仿真
图3给出了XWG1模拟发送5组正误对比H′,经过译码得到5组G,用逻辑分析仪XLA1仿真时序关系.如XWG1中当H′=H时,XLA1的310 ms后1个周期内G=00000,表示无误.当H=1110001011010时,XLA1中350 ms后的G=10011,表明H3出错,再用纠错电路取反即可.与方程组(4)所求值相符.
(2) 纠错电路.根据逻辑量同或运算法则:HΘ0=H的非,HΘ1=H.将H′中M′与G对应的8种(如表2)有效情况进行同或运算,即可得到正确的M.其验证结果如图4所示.
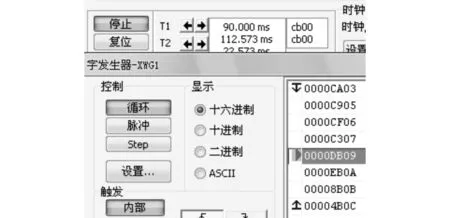
图4 SEC-DED码指误字时序仿真
图4清楚给出Mi的8种1位出错都可纠正,其中隐含当M′=M时,无误情况.
3 结语
本文提出了基于FPGA实现SEC-DED海明校验码的硬件实现方案,基于Multisim 11.0软件将编码、译码和纠错3部分整合成一个系统,经过仿真、验证,对确定的FPGA编译配置后,该系统占用资源少,校验可靠、高速.该系统自成一体,用户只需对接口进行操作.因此,它即可独立使用,亦可配合其它系统作为其校验模块使用.
[1]Robert H M.纠错编码的艺术[M].2版.张立军,译.北京:北京交通大学出版社,2007:8-30.
[2]Whitman M E,Mattord H J.信息安全原理[M].北京:清华大学出版社,2003.
[3]潘 松,黄继业.EDA技术与VHDL[M].3版.北京:清华大学出版社,2010:182-210.
[4]吕志鹏.16位微处理器在FPGA上的设计与原理实现[D].北京:清华大学,2004.
[5]常海天,胡 鉴.基于FPGA的CRC并行算法研究与实现[J].微处理机,2010(2):45-48.
[6]王冠华.Multisim 11电路设计及应用[M].北京:国防工业出版社,2010:140-159.
[7]Davide P,Scott T.Practical FPGA programming in C[M].Boston:Prentice Hall PTR,2007:45-60.
[8]王文剑,熊永中,唐良义.基于ISE和Modelsim的汉明码设计[J].自动化技术与应用,2010,29(3):54-57.[9]王习东,陈重江,陈志勇.基于FPGA的线阵CCD驱动电路设计[J].三峡大学学报:自然科学版,2010(3):77-79.

