规则空间模型在考试评价中的应用——以小学五年级分数图形测验为例
田霖 刘儒德
规则空间模型在考试评价中的应用
——以小学五年级分数图形测验为例
田霖 刘儒德
规则空间模型(RSM)是一种将认知心理学和心理计量学相结合的认知诊断模型,可用于识别被试的属性掌握模式(即知识结构)及诊断被试解题过程中的认知错误。本研究应用规则空间模型对小学五年级学生的分数知识结构(包括6个属性)进行认知诊断,最终将386名被试判归入26种属性掌握模式。规则空间模型对于大规模考试实践具有重要指导意义,考试管理机构应借鉴规则空间模型的思想,提高命题质量、改进分数报告,更好地发挥考试的教育功能。
规则空间模型;认知诊断;属性掌握模式;大规模考试
传统考试更多的是依据总分对学生进行排队,缺乏对考试信息的深度挖掘[1]。认知诊断理论作为新一代测量理论的核心,将学生解答试题的认知过程融合到测验模型中,着眼于个体潜在知识结构与作答过程之间关系的研究,可为教学与学习过程提供更多的诊断性信息[2][3]。Tatsuoka的规则空间模型(Rule Space Model,RSM)将认知心理学、项目反应理论和数据库的代数理论相结合,运用了泛函分析、布尔代数和多元统计等多方面的知识,能够有效地诊断被试的认知错误[4]。本研究将规则空间模型的方法引入小学五年级学生分数学习的错误诊断研究中,考察学生的分数知识结构特点,并进一步探讨规则空间模型对考试评价实践的启示。
1 规则空间模型简介
规则空间模型是将被试在测验项目上的作答反应划归为某种与认知技能相联系的属性掌握模式的统计方法[5],该技术主要用来处理潜在认知属性变量[6]。模型的基本假设认为,测验项目可以用特定的属性描述,属性包括被试正确求解测验项目所必须具备的知识点、技能、策略、认知加工过程等[7],规则空间模型使用Q矩阵来表征试题与属性之间的对应关系(即试题涉及的属性)、用属性掌握模式来表征个体的知识结构。属性掌握模式通常不可直接观察,需要基于Q矩阵将其转化为可观察的理想反应模式,然后基于一定的规则将考生的实际反应模式(观察模式)判归为某种特定的理想反应模式,从而完成对考生知识结构的诊断。
规则空间模型的判别过程分为两个阶段。第一阶段是分析、确定不可观察的知识结构(即属性组合方式),并用可观察的项目反应模式进行表征。具体操作为:①确定所要测量的认知属性及属性间的层级关系。②开发诊断性测验,将属性与项目进行关联,建立Q矩阵(反映测验项目与属性的对应关系)。③基于Q矩阵,生成邻接矩阵A(反映属性间的直接关系),通过对A进行布尔加法和乘法运算获得可达矩阵R、典型属性矩阵Ea(即属性掌握模式),进而获得理想反应模式。理想反应模式是指被试始终一贯地使用同一规则的情况下的得分模式,即假定不存在猜测或失误时考生的得分情况[8]。
第二阶段是建构规则空间,应用统计分类方法对被试的实际反应模式进行判别,并且计算被试的属性掌握概率。具体操作为:④建构由被试能力θ与异常反应指标ζ构成的二维坐标系,即规则空间,其中横纵(θ)代表被试能力水平(基于IRT的能力值),纵轴(ζ)代表异常反应程度(也称警戒参数,反映实际反应模式与理想反应模式的差异)。ζ是函数 f(x)的标准化形式,f(x)=[P(θ)-X]*[P(θ)-T(θ)],其中P(θ)=[p1(θ),p2(θ),…,pn(θ)],X是被试的项目反应向量,T(θ)=[T1(θ),T2(θ),…,Tn(θ)],通过计算可知,f(x)的期望值为0,方差,定义。通过将理想反应模式以一组序偶{(θ,ζ)}映射在规则空间内,即可获得纯规则点(θR,ζR)。⑤建立分类标准,将考生的实际反应模式按照④中的方法映射到规则空间内,即待判别的观测点(θX,ζX),然后应用贝叶斯分类程序进行判别,将被试判归入具有最小马氏距离和最大后验概率的知识结构中。⑥计算特定被试的属性掌握概率,属性掌握概率的计算考虑到了与考生距离在一定范围以内的多个知识结构,是多个属性掌握模式中特定属性掌握概率的加权平均数。
2 研究方法
2.1 属性确定与测验编制
本研究的测验主要用于诊断小学五年级学生在分数学习初期的知识掌握情况(解决分数图形问题所需掌握的知识或技能)。通过与小学数学教研员、小学数学教师进行深入讨论,本研究最终确定了五年级学生正确解决分数图形问题所需要的6个属性(见表1)以及属性间的层级关系(见图1),属性的界定严格依据《小学数学课程标准》中的有关内容[9]。

表1 属性列表

图1 属性层级关系
确定属性及其层级关系后开始编制诊断性测验。测验编制过程在小学数学教研员的指导下进行,并参考已有的分数图形题库中的优秀试题。本研究选取45名五年级学生作为样本进行试测,最终正式测验保留27道试题,全部为客观题。采用0-1计分方式进行评分(错误作答或未作答均得0分,正确作答得1分)。采用项目反应理论双参数logistic模型进行项目参数估计,获得27个测验项目参数如表2所示。

表2 项目参数
2.2 样本与施测
选取北京地区3所小学五年级学生共400人(男215,女185)为正式施测对象,施测时被试尚未学习通分的知识内容,已掌握分数的意义与基本性质,会进行同分母分数的加减运算及简单分数大小比较,能借助图形进行分数化简;施测方式为集体施测;测试时间为40分钟;本次施测共发放测验卷400份,回收有效答卷386份(有效测验回收率为96.5%)。
2.3 数据处理工具
测验的项目参数以及被试能力参数的估计,采用IRT统计软件(ASCII Item and Test Analysis Pack⁃age);规则空间模型的有关参数采用北京师范大学心理学院心理测量与评价课题组开发的规则空间模型运算程序。
3 结果与分析
3.1 Q矩阵、邻接矩阵A、可达矩阵R
将本测验中27道试题与6个认知属性相关联,生成Q矩阵,Q矩阵中1代表试题涉及该属性,0代表试题不涉及该属性,如表3所示。Q矩阵反映了测验中试题考核的属性,即被试正确作答试题所需要掌握的分数知识或技能。
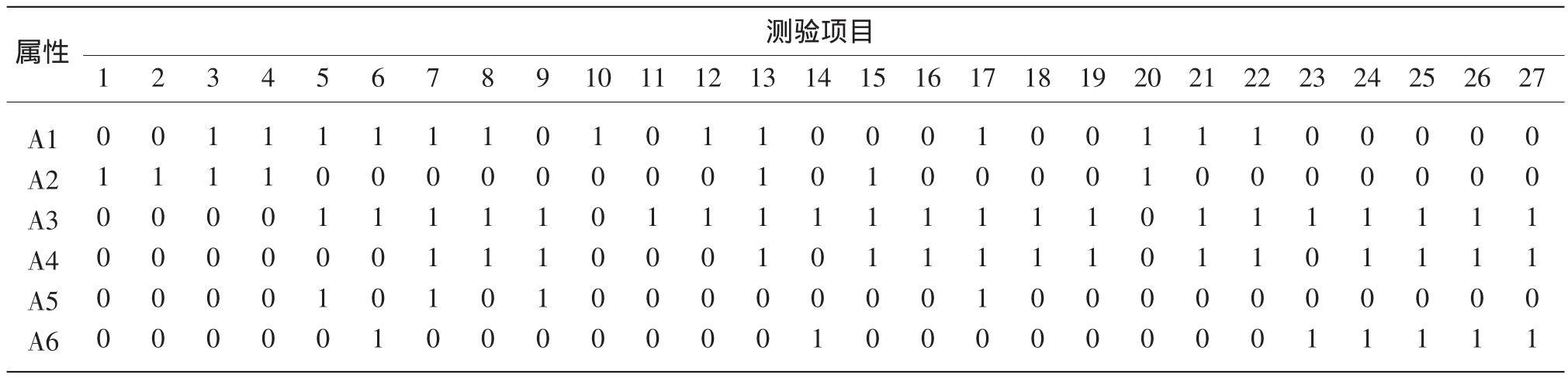
表3 项目-属性关联Q矩阵
基于本研究考查的6个属性生成邻接矩阵A,其反映属性间是否存在直接逻辑关系,矩阵中0代表不存在,1代表存在,如表4所示。基于Q矩阵及A矩阵获得可达矩阵R,其反映两个属性间是否存在直接关系或间接关系,矩阵中0代表不存在,1代表存在,如表5所示。
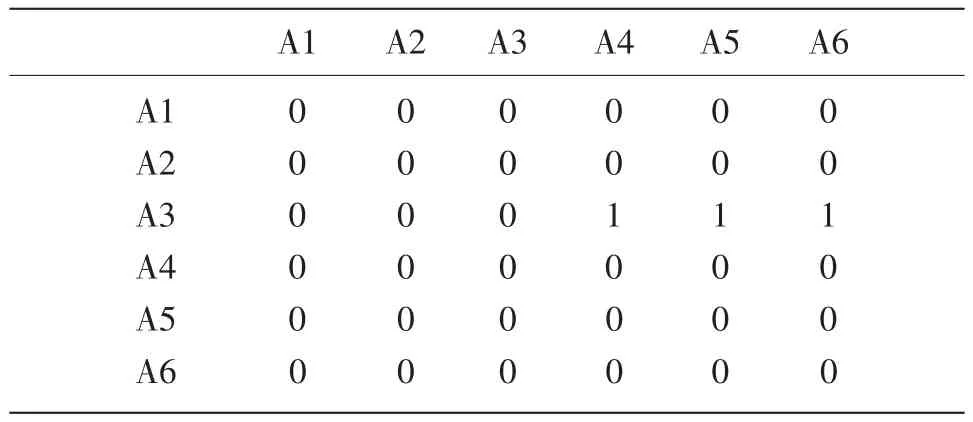
表4 邻接矩阵A

表5 可达矩阵R
3.2 典型属性矩阵Ea与理想反应模式
典型属性矩阵Ea由代表属性掌握模式的一组向量构成,是依据属性层级关系所能获得的所有合理的属性组合方式,代表考生的知识结构。典型属性矩阵Ea中0代表被试未掌握该属性,1代表被试掌握该属性。基于Q矩阵、A矩阵及R矩阵,本研究得到32种属性掌握模式,对应于32种知识结构(其中“000000”代表被试未掌握任何属性,“111111”代表被试掌握了全部6个属性),基于Q矩阵及Ea矩阵生成与属性掌握模式对应的32种理想反应模式,即当被试不出现失误或猜测时在本测验27道试题上的作答反应。在理想反应模式中,用一组理想反应向量构成的矩阵表示被试的作答反应,矩阵中0代表作答错误或漏答,1代表作答正确。为了便于说明,表6中同时给出典型属性矩阵Ea与理想反应模式。规则空间模型可预测被试在测验项目上的理想作答情况,从而预测被试的理想测验得分,表6中给出了具有不同知识结构的被试在本测验中的理想得分。
3.3 纯规则点的位置参数及判别结果
本研究选用双参数项目反应模型对被试能力参数θ和项目参数a、b进行估计,应用规则空间模型运算程序对警戒参数ζ进行估计,最终获得代表理想反应模式的32个纯规则点(θR,ζR)的位置参数,应用同样方法可获得386个观测点(θX,ζX)的位置参数(由于篇幅过程,此处略),同时计算被试的属性掌握概率,依据最小马氏距离与最大后验属性掌握概率原则对观测点进行判别。为了便于说明,表7中同时给出32种理想反应模式对应的属性掌握模式、被试能力值θ、异常指标ζ、判别人数及所占百分比。
从表7中的判别结果可以看出,386名被试被判归入26种属性掌握模式内。其中被判别为P26,P25,P21,P22,P30,P 20,P31知识结构的被试较多,分别占11.14%,10.36%,9.59%,8.81%,7.77%,反映了大部分被试的知识结构特点;掌握全部属性P32的被试人数较少,占4.40%,即分数知识的初学者同时掌握全部6个属性较为困难;而P01、P02、P03、P04、P06、P19这6种知识结构的判别结果为0;P05、P08、P10、P11、P12、P14、P16、P18这8种知识结构的判别结果均小于5。对386名被试的属性掌握情况进行分析,可发现分数学习初期五年级学生对属性A1~A6的总体掌握率依次为59.84%、69.69%、98.70%、83.42%、50.04%、58.03%,表明学生对“读取图示分数”、“分数化简”、“确认等分”等属性的掌握较好,而对“比较分数大小,”“辨别单位1”、“进行加减运算”等属性的掌握则相对较差。
判别结果表明了被试的属性掌握模式(知识结构)特点,同时也反映了被试知识结构中存在的认知缺陷,这种认知缺陷在测验中表现为作答失败。通过事后访谈发现,虽然“辨别单位1”总体掌握率较低,但被试并不认为掌握该属性存在困难,测验中的作答失败常常是由于在解题时忽略“辨别单位1”而造成的;而当两个代表单位1的图形不同时被试进行“比较分数大小”存在困难,被试容易受到图形本身特征(如面积大小、等分方式等)的影响而产生作答障碍;当“读取图示分数”、借助图形进行“分数大小比较”或“加减法运算”等多个认知操作过程同时考核时,较高的认知负荷使被试容易因为某个中间环节的失误而导致作答失败,即同时应用多个属性解题对于分数知识的初学者具有更高的挑战。
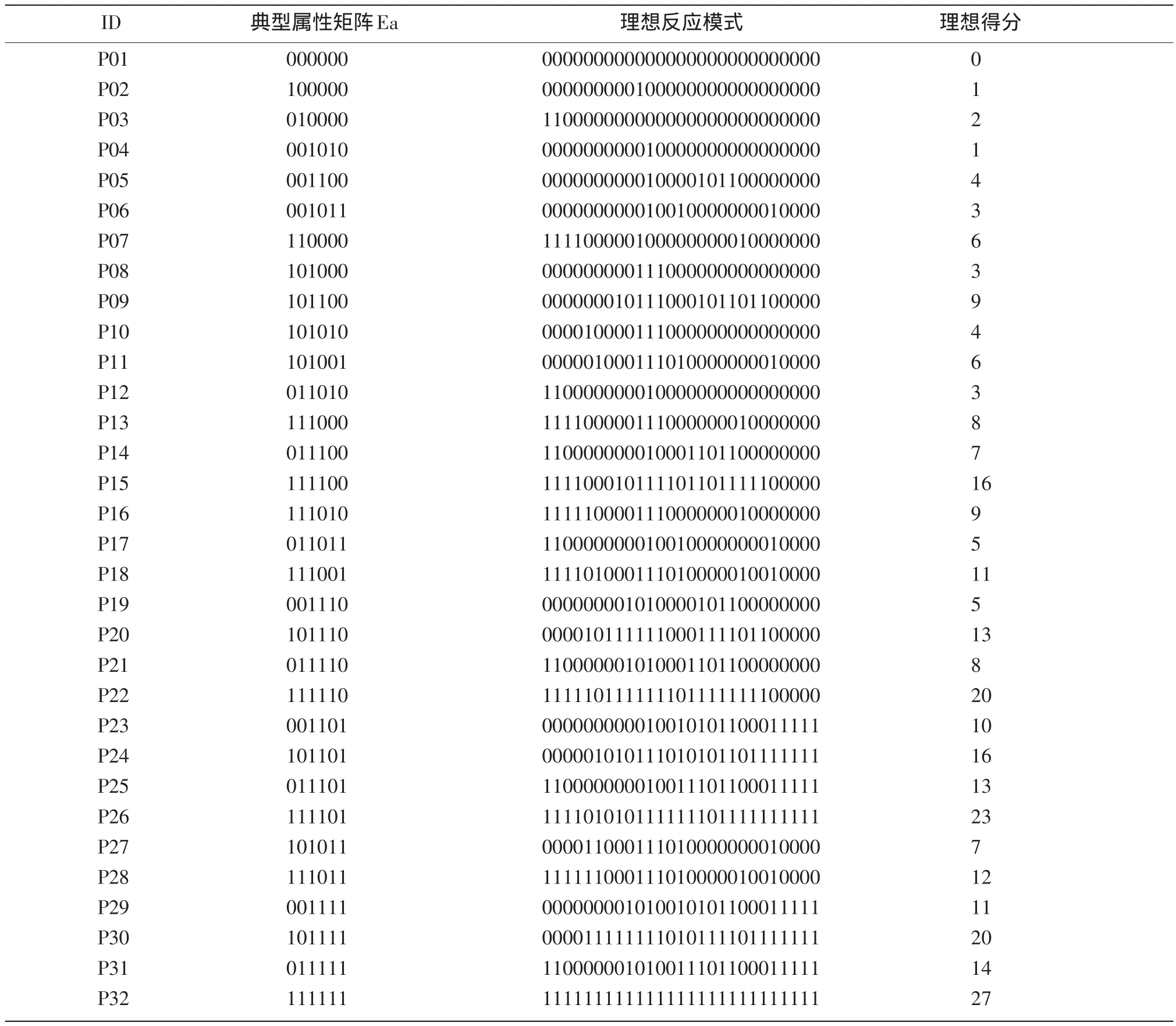
表6 典型属性矩阵Ea、理想反应模式、理想得分
4 结论与反思
基于实证研究结果得到如下结论:应用规则空间模型能够对小学五年级学生在分数学习初期阶段解决分数图形问题的知识结构(6个认知属性)进行有效诊断,将386名被试判归为26种属性掌握模式,而且规则空间模型可用于识别学习者的分数知识结构的缺陷及错误类型,为教师制定补救性教学策略提供依据。
现代学业评价认为在考试的基础上对学生的认知结构进行诊断是非常必要的[10]。规则空间模型的思想对于在大规模考试实践中开展认知诊断提供了重要借鉴意义。考试管理机构应借鉴诊断性测验的思想指导命题实践,提高测验的诊断功能与内容效度[11];深入挖掘考试数据,改进分数报告反馈方式,如在分数报告中向考生提供更多的诊断性信息、提出认知策略的改进建议、内置启发性问题引发学习者反思、采用积极的反馈效价等[12],为促进有效教育提供更好的服务。
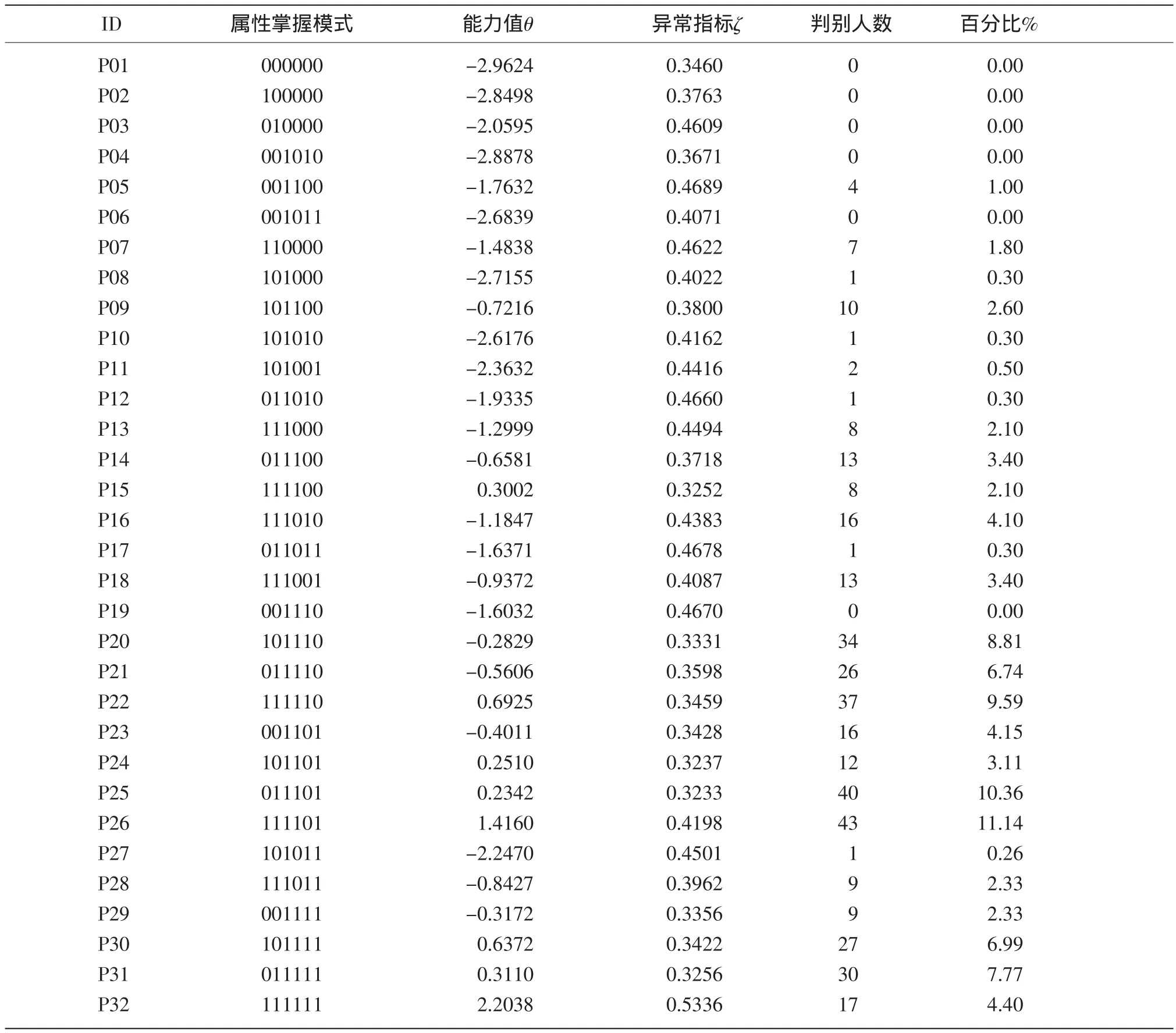
表7 纯规则点的位置参数及判别结果
目前国内有关规则空间模型的研究多集中在模型自身的发展及数据模拟分析,规则空间模型的应用研究也局限于属性数量少、属性层级关系清晰的知识领域内。将规则空间模型应用于大规模考试实践(如中学会考、自学考试、语言水平考试等)中仍存在诸多问题,如有关0-1评分试题的模型研究较为成熟,而大规模考试中也包含多级评分试题(如论述题、写作题等),如何开发适用于多级评分方式的模型;本研究中只涉及分数学习初期6个属性,属性的界定较为容易,而对于某些课程结业考试(如自学考试、高校中的专业课考试等),其命题依据主要是教材与考试大纲,对于章节繁多且知识体系庞杂的测量内容,如何选择并界定认知属性;规则空间模型基于被试的作答表现(错误)对其属性掌握情况进行诊断,然而导致试题作答错误的具体原因可能包括多种类型,如信息缺乏、启动错误、知识点混淆、规则应用错误等[13],如何根据诊断结果确定作答错误的具体原因;随着计算机辅助考试与网上阅卷技术的发展,如何开展基于计算机的认知诊断等,这些问题需要研究者进行更为深入的探讨。
[1]辛涛.新课程背景下的学业评价:测量理论的价值[J].北京师范大学学报(社会科学版),2006(1):56-61.
[2]Tatsuoka K.K.Rule space:An approach for dealing with miscon⁃ception based on item response theory.Journal of Educational Mea⁃surement[J].1983,20(4):345-354.
[3]Nichols,P.D.A framework for developing cognitively diagnostic assessment.Review of Educational Research,1994,64:575-603.
[4]余嘉元.运用规则空间模型识别解题中的认知错误[J].心理学报,1995,27(2):196-203.
[5]Gierl M J,Leighton J P,Hunka S M.Exploring the logic of Tatsuo⁃ka’s Rule-Space Model for test development and analysis,Educa⁃tional Measurement:Issues and Practice.Fall 2000:34-44.
[6]辛涛,焦丽亚.测量理论的新进展:规则空间模型[J].华东师范大学学报(教育科学版),2006(3):50-56.
[7]戴海崎,张青华.规则空间模型在描述统计学习模式识别中的应用研究[J].心理科学,2004(4):949-951.
[8]Tatsuoka K.K.,Tatsuoka M.M.Bug distribution and statistical pattern classification[J].Psychometrika,1987,52(2):193-206.
[9]全日制义务教育数学课程标准(实验稿)[M].中华人民共和国教育部编制.北京:北京师范大学出版社.2001.
[10]涂冬波,漆书青.认知诊断与大规模统一考试的改革[J].教育与考试,2007(1):38-41.
[11]刘声涛,戴海崎,周骏.新一代测验理论—认知诊断理论的源起与特征[J].心理学探新,2006(4):73-77.
[12]田霖,王桥影.反馈研究对改进教育考试分数报告的启示[J].考试研究,2011(1):65-71.
[13]Butler,D.L.&Winne,P.H.Feedback and self-regulated learn⁃ing:A theoretical synthesis.Review of Education Research,1995,65(3):245-281.
Applied Research of RSM in Test of Figure-presented Fraction for the Fifth Grade
TIAN Lin and LIU Rude
Rule Space Model(RSM for short),which combines with the cognitive psychology and psychometrics,is used to identify students’attribute-mastery patterns(knowledge structure)and diagnose cognitive errors during problem-solving.This paper applied RSM to diagnosing fifth-graders’fraction-knowledge structure,which involves 6 cognitive attributes,and classified 386 test-takers into 26 different fraction-knowledge structures according to their actual response patterns.RSM provides great technical support and guidance to large-scale examinations and Educational examination authority should improve test construction and score report based on the research accomplishment of cognitive diagnosis,so as to promote educational function of examination.
Rule Space Model;Cognitive Diagnosis;Attribute-Mastery Pattern;Large-Scale Examination
G405
A
1005-8427(2012)08-0016-7
本研究得到北京师范大学心理学院心理测量与评价课题组成员的帮助,谨致谢意。
北京教育考试院
北京师范大学

