基于分层线性模型的我国城市居民体育锻炼行为研究
宁科,马云霞,李晓天
(1.陕西教育学院 体育部,陕西 西安 710061;2.伊犁师范学院 体育学院,新疆 伊犁 835000;3.首都体育学院,北京 100191)
基于分层线性模型的我国城市居民体育锻炼行为研究
宁科1,马云霞2,李晓天39
(1.陕西教育学院 体育部,陕西 西安 710061;2.伊犁师范学院 体育学院,新疆 伊犁 835000;3.首都体育学院,北京 100191)
使用CGSS2006城市问卷部分数据,采用分层线性模型对我国城市社区居民的个体体育行为进行了研究。研究认为,个体层自变量个人每周工作时间、受教育年限、个人年收入与高层自变量家庭月收入共同作用影响个体体育锻炼行为的发生;此外在排除个体层自变量的影响,家庭层的家庭月支出对个体体育锻炼行为的发生有决定性的影响。
社会体育;体育锻炼行为;城市社区;分层线性模型;中国
在社会科学中,很多研究问题都体现为多水平、多层的数据结构。其中最为典型的例子就是在教育研究中。同样,人们体育锻炼行为的发生不仅受到个体水平层变量的影响,还受到高层家庭变量的影响。现有文献中的城市居民体育锻炼行为研究相当少,仅有的文献研究脉络为在个体自变量的基础上选取自变量建立统计模型分析,但将不同类型的影响因素纳入同一模型进行回归分析就可能产生分析结果异常等问题,原因在于影响人们体育锻炼行为的因素之间可能存在分层结构现象,很可能导致生态谬误的风险[1-2]。影响人们体育锻炼行为的分层结构决定了体育锻炼行为的产生与否,单个人的体育锻炼行为必然会受其个体的社会经济、教育等因素的影响,同时更高层次的家庭组织和社区环境、家庭经济状况、生活区域环境质量等也可能会对其体育锻炼行为产生影响。
分层线性模型不仅在技术上是先进的,而且比一般线性回归具有更大的包容性。一般意义上回归分析实际上仅能对单一分析单位进行处理[3-4],开展变量之间关系的研究。大多数其他统计方法也都默认这种平面数据结构。这类统计方法背后存在一个重要假定,即各案例之间都是完全独立的。但这种假定与社会现实之间有差异,因为通常这些案例隶属于不同的组群。不同组群之内的案例相互影响、并不独立,往往存在很强的同质性,又可称为组内相关。各组群之间又往往存在着明显的差别[5-6]。本研究采用分层模型分析方法,以分层线性模型中随机效应模型为基础,在此基础上延伸随机系数模型与截距、斜率模型,重点研究以下几个问题:个体的体育锻炼行为是否受到家庭层因素的影响;个体水平的自变量与家庭层的自变量对个体体育锻炼行为产生的影响是否有交互作用;家庭层自变量与个体体育锻炼行为之间是否有相关关系。通过研究以期为提高我国城市社区居民体育锻炼行为研究提供理论上的帮助。
1 研究对象与方法
1.1 问卷调查
该项目本次调查采用分层的 4阶段不等概率抽样:区(县)、街道(镇)、居委会、住户和居民,在全国28个省市抽取10 000个家庭户,然后在每个被选中的居民户中按一定规则随机选取1人作为被访者。本研究问卷来自CGSS2006城市问卷,问卷由香港中文大学与中国人民大学共同设计。该问卷经过权威专家设计,并经过科学验证,目前属于国内先进的综合社会学调查问卷。问卷中体育锻炼的题项调查意在统计过去一年中有无体育锻炼行为的中国国民。问卷的原题目为:“你在闲暇时间中,从事体育锻炼的活动频率是”,选择答案为:1)差不多每天;2)一周几次;3)一月几次;4)一月一次;5)一年几次;6)从不。将答案题项进行整合,一周几次、一月几次、一月一次、一年几次整合为锻炼,“从不”定义为不锻炼。以此纳入模型进行运算。分层模型分析采用HLM 6.06软件。本研究根据研究设计要求对数据进行删失处理,最终保留2 647个样本,其中女性样本1 276个(占48.2%),男性样本1 371个(占51.8%)。
1.2 研究假设
人们体育锻炼行为的发生受到很多变量的影响。在已有的研究文献中有学者认为城市各阶层居民体育锻炼参与程度与其阶层存在显著性差异,阶层越高参与度越高;其次,有研究者从家庭环境视角发现,父母受教育程度越高大学生余暇体育锻炼行为越低;父母参加锻炼越高对大学生余暇体育锻炼行为影响越大[7-9]。可见,当前研究文献没有涉及个体体育锻炼行为的发生是否受教育年限、每周工作时间、个人年收入等的影响。其次,当前研究仅是个体水平面的数据研究,基本未涉及高层变量对低层——个体层体育锻炼行为发生是否有影响的研究。最后,对于多个自变量共同影响因变量研究中,基本未涉及自变量之间的交互作用对因变量的影响,特别是高层与低层的交互作用对因变量的影响。基于以上分析本文设立如下假设:
假设 1:性别对个人体育锻炼行为有影响,且回归系数受到高层自变量的影响;
假设 2:个体体育锻炼行为受教育年限影响,且回归系数受到高层自变量的影响;
假设3:周工作时间对个人体育锻炼行为有影响,且回归系数受到高层自变量的影响;
假设4:个体体育锻炼行为受到个人年收入影响,且回归系数受到高层自变量的影响;
假设 5:个体体育锻炼行为受到家庭全年总收入的影响;
假设 6:个体体育锻炼行为受到家庭年教育费用的影响;
假设 7:个体体育锻炼行为受到家庭月基本生活费的影响;
假设 8:个人体育锻炼行为受到家庭年医疗费的影响;
假设 9:家庭月支出对个体体育锻炼行为具有直接影响(截距)。
1.3 研究模型设计
1)研究变量选择。
本研究在个人层面上的自变量为个人年收入、个人每周工作时间、性别、个人受教育年限;家庭层面变量为家庭年收入、家庭月基本生活费、家庭年医疗费、家庭年教育费用(表 1、2为各层自变量的描述统计结果)。

表1 个体水平自变量、因变量变量描述性统计

表2 家庭层变量描述性统计
2)随机效应的单因素方差分析。
本文所涉及的因变量是指体育锻炼行为,其中“0”为不锻炼,“1”为锻炼。第一步是应用分层模型分析随机效应的单因素方差,主要步骤:在模型各层中不插入任何解释变量,对分层数据进行无条件方差分解分析,通过分析结果可以将因变量的总方差分解到模型的不同层,观察两层随机方差分别在总方差中的比例分布,便可以确定进行分层分析的必要性[10]。采用HLM软件来进行人们体育锻炼的分层分析。以本研究为例,层1为个人,层2次为家庭,层1的模型与传统的回归模型类似,与一般回归方程有区别的是,每个个人的回归方程的截距和斜率都直线依赖于层2次变量(家庭收入、支出等),这样就构成了个人-家庭 2层模型。
层1模型(个人层):

层2模型(家庭层):

其中,η代表因变量,twosport代表体育锻炼行为,φ代表参加体育锻炼的概率,β代表回归系数,log代表取对数,μ0代表残差,γ00代表截距。
层1模型中由于因变量η取值1时代表参加锻炼,所以模型中的φ就是参加体育锻炼的概率。这说明体育锻炼行为的总方差中高层变量方差(即层2家庭方差)所占比例越大,用高层变量来解释的可能性就越大。
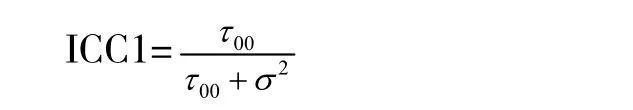
其中(τ00代表随机回归,σ2代表方差。)
组内相关数ICC1=0.21>0.05,说明有21%的变异来自家庭(即组间变异),79%的变异来自个体变量,说明数据存在层级效应[11]。根据研究需要在模型中的两层纳入自变量后的全模型进行运算。
2 研究结果与分析
2.1 带随机效应的单因素方差模型
全模型(即层1与层2叠加起来的组合模型,本文中主要用于研究层1因变量怎样受到层2和层1的自变量的影响),在层1与层2纳入了研究所涉及的自变量。该模型所构建的研究假设主要指:认为人们的体育锻炼行为的发生是由于分属于不同经济收入水平的家庭类型,其体育锻炼行为的产生存在差异。从统计上分析这种差异的表现就是家庭支出的不同会导致个体体育锻炼行为状况存在显著不同。全模型如下:

其中,gender代表性别、eduyear代表受教育年限、weekhours代表每周工作时间、indincome代表个人年收入、twosport代表体育锻炼行为、famincome代表家庭收入、farmhouse代表家庭医疗费用、famedu代表家庭年教育支出、fammof代表家庭月支出。上述变量除性别为分类变量外,其他全部为连续变量。γ00是个体水平模型的截距,由于连续变量都按家庭的平均值对中,因此截距在这里代表着各家庭的个人体育锻炼行为。β0代表自变量的截距,β系数与一般回归系数的解释方式相同。引入高层自变量——家庭层的家庭年收入、家庭月基本生活费、家庭年医疗费、家庭年教育费用的自变量之后,家庭月基本生活费显著,其他高层自变量对因变量不显著。方差成分由层1模型的0.130 51减少到0.020 18,从纳入家庭层的自变量与个体层的自变量来说,模型的方差降低,说明模型分层效应明显。
假设认为,城市社区中人们体育锻炼行为是由个人特征和所处背景共同作用的结果。家庭的背景变量包括该家庭的年收入、月支出、家庭年教育支出等这可以作为代表个体所在家庭的经济和社会状况指标。家庭收入的标准差(s=26 500.43)其实都是比较大的,反映出城市社区中的家庭经济不同。
从表3发现高层变量中仅有家庭月支出显著,其他变量不显著。层1中的性别与个人年收入不显著对个体体育锻炼行为没有影响,这一点与前人研究结果一致。个人的受教育年限与每周工作时间对体育锻炼行为的发生有显著影响。随机效应的单因素方差模型中的β0是体育锻炼行为发生比。模型参照类(虚拟变量取0值)为不锻炼。个人层回归方程的截距值取决于高层自变量——家庭月支出(即β0=γ02×fammof),β0说明家庭支出越大其体育锻炼行为的发生比越高。γ02对应的发生比为0.918,表明在控制其它变量不变当家庭月支出提高1元钱(即从0变为100%时),它导致社区居民体育锻炼行为发生比变化 0.918倍,这是家庭月支出对体育锻炼行为发生的直接影响的一种统计归纳。这里并不是说家庭月支出越多就是人们参加体育锻炼的原因,而是说在存在体育锻炼行为偏好为既成事实的条件下,家庭月支出提高,个人就容易参加体育锻炼。从模型回归系数(表3中回归系数——0.009 0)为正值即提高家庭月支出可以促进社区居民体育锻炼行为发生比的可能性会提高。个体层的自变量,受教育年限与每周工作时间显著(P<0.001),受教育年限的回归系数为正值,即为提高受教育年限会促进社区居民参加体育锻炼,表明在控制其它变量的情况下,个体受教育年限每提高1年,它导致个体体育锻炼行为变化 1.068倍。此外,每周工作时间显著(P<0.001)。表明样本可以向总体推断,值得注意的是每周工作时间的回归系数为负值-0.020 8,即为减少每周工作时间会促进个体参加体育锻炼,它表明个体每周工作时间每减少1 h,它导致社区居民体育锻炼行为发生比变化0.879倍,该统计归纳表明个体每周工作时间减少,个人就容易参加体育锻炼,这和现实情况一致。当前困扰我国城市居民参加体育锻炼的因素当中,没有时间参加体育锻炼就是首要影响因素之一。
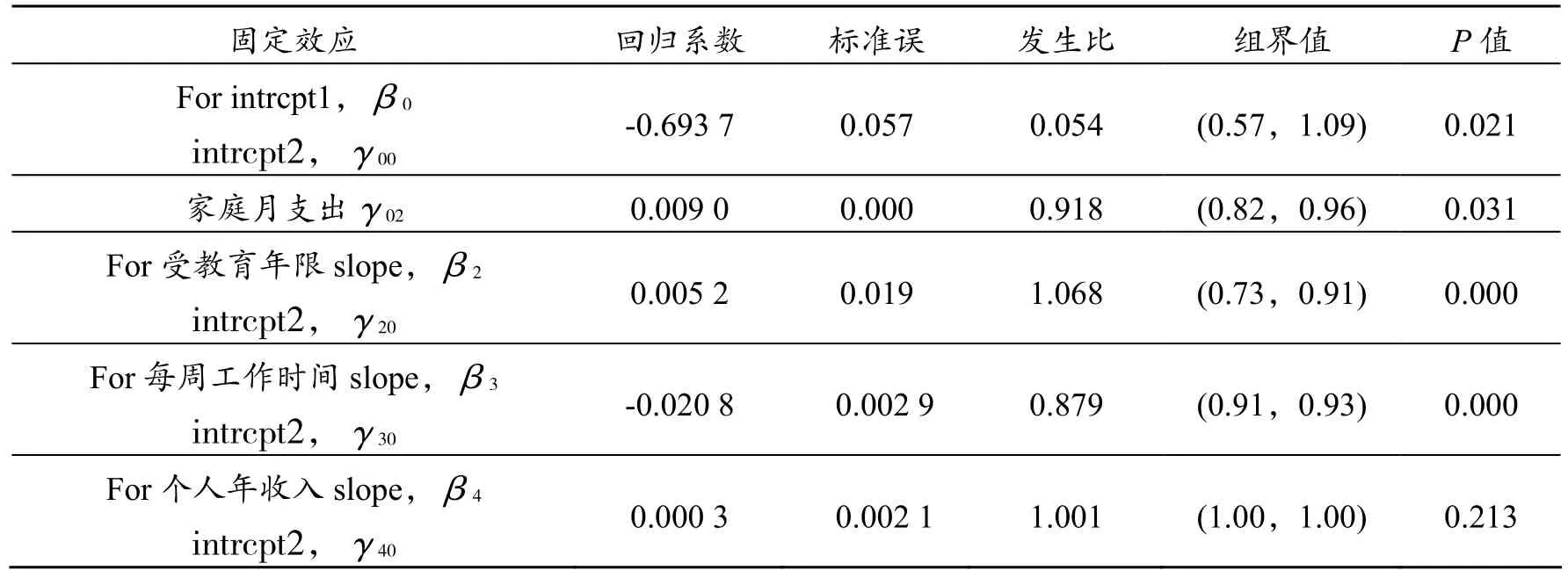
表3 随机效应的单因素方差全模型回归系数(固定效应)1)
除掉不显著的变量后,模型重新整合为:
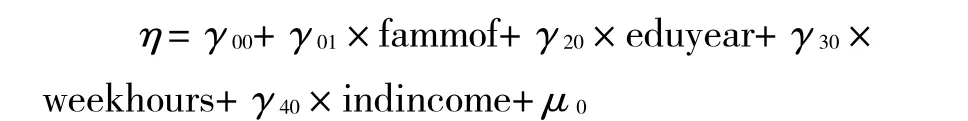
2.2 以截距和斜率为结果的模型
以模型为基础,进行更深一步的分析。一般线性回归中对于截距及斜率的解释力度非常小,截距只是作为一个常数项,常数项反映在坐标就是最小二乘的直线在y轴上的高度,而分层线性模型通过数学理论将截距的解释分解到层2的自变量进行解释,斜率也是分解到层2的自变量进行解释[12-13]。此处在单因素方差模型的基础上重点对截距及自变量的斜率进行分析。

其中,γ01、γ02、γ11、γ21、γ31代表截距。
一般线性回归中截距包含很多信息。对于本研究中的分层线性模型中的截距解释就是,为何不同家庭中的个人体育锻炼行为发生率不同。那么分层线性模型就会对截距进行解释,解释是通过将截距纳入层 2的家庭月支出与其斜率即自身的截距来分解层 1截距,表4中固定效应模型表示在模型(2)中的层1自变量的截距β0,这在分层模型中属于截距斜率模型。通过层2的平均家庭月支出来进行预测,模型运行显示家庭月支出与个人体育锻炼行为发生正相关,家庭月支出γ01=0.005 2,P<0.001。家庭月支出是可以预测模型中截距(截距是随机的),简单的说,在层 1模型其他自变量(自变量:受教育年限、个人年收入、每周工作时间)选择为零时,家庭月支出对个体体育锻炼行为发生率有影响也就是说家庭支出决定了个人体育锻炼行为的发生。这与上个小节的分析结果基本一致。这也表明了家庭月支出是形成层 1截距有效解释力之一。斜率模型表示在模型(2)中的层1的自变量的斜率即β1、β2、β3是否可以通过层 2的平均家庭月支出有效预测个人体育锻炼行为的各个自变量的斜率。模型运行显示,受教育年限γ11、每周工作时间γ21、个人年收入γ31通过层 2家庭支出自变量的预测发现是可以预测斜率β1、β2、β3,但是需要注意的是斜率表现在模型(3)中是交互效应,即层1自变量与层2自变量共同作用来影响层1的自变量的各个斜率即模型中的回归系数是层1自变量与层2自变量共同作用的结果。

表4 以截距和斜率作为结果模型
3 讨论
本研究所做的假设1(性别对个人体育锻炼行为有影响),经过模型运算发现未得到验证。假设2(个体体育锻炼行为受到受教育年限影响,且回归系数受到高层自变量的影响),经过分析得到验证:受教育年限影响个体体育锻炼行为的发生,且回归系数受到高层自变量家庭月支出及受教育年限低层自变量的交互影响。假设3(周工作时间对个人体育锻炼行为的产生有影响,且回归系数受到高层自变量的影响)。经过分析得到验证:每周工作时间对个人体育锻炼行为的产生有影响,且回归系数受到高层自变量家庭月支出及低层自变量——每周工作时间的交互影响。假设4(个体体育锻炼行为受到个人的年收入影响,且回归系数受到高层自变量的影响)经过分析得到验证:个人年收入对个人体育锻炼行为的产生有影响,且回归系数受到高层自变量家庭月支出及低层自变量——个人年收入的交互影响。假设5(个人体育锻炼行为受到家庭全年总收入的影响)、假设6(个人体育锻炼行为受到家庭年教育费用的影响)、假设7(个人体育锻炼行为受到家庭月基本生活费的影响)、假设8(个人体育锻炼行为受到家庭年医疗费的影响)、假设9(家庭月支出对个人体育锻炼行为具有直接影响作用),经过模型运算发现得到验证。
从验证的模型中的自变量发现,体育锻炼行为的发生受到个人年收入、每周工作时间、个人受教育年限及高层自变量——家庭月支出的共同影响,换句话说,这是一个自变量的共同作用导致体育锻炼行为发生的结果。而不显著的自变量并不是说无效,而是相对于显著的自变量来说,不显著的自变量对体育锻炼行为的发生作用效力非常小。此外,也说明模型不能由样本向总体推断。本研究中的重点之一截距即层 1模型中所有自变量全部取值为零时,个人体育锻炼发生率,通过截距斜率模型分析认为,这是由于高层自变量家庭月支出所致,家庭月支出与个人体育锻炼行为发生率呈现相关性。最后,对于研究所涉及层1自变量的斜率,通过模型拟合发现层1的自变量的斜率均是其本身与高层自变量家庭月支出交互作用结果。
首先,对个体体育锻炼行为发生在个体层面和家庭层面的零模型结果表明,不同家庭的月支出存在差异,证实了有必要进行分层研究的必要。个体受教育年限、年工资收入、每周工作时间对体育锻炼行为产生影响。但是这不是其个人特征完全决定的,家庭作为影响一个人的重要环境——家庭月支出对个人的体育行为产生重要的影响(零模型中家庭层面消减了21%的方差)。其次,通过解释性分层线性模型的分析,本文利用实际调查数据中的信息对体育锻炼行为在个人层和家庭层的影响因素进行了初步探索。结果表明,体育锻炼行为的确是多层因素共同作用的结果,并且各层影响因素之间还存在着复杂的互动机制,即层 1自变量的斜率是该自变量与层2自变量共同交互作用所致。最后,截距模型的模型拟合表明个人体育锻炼行为发生与家庭月支出呈现正相关,家庭月支出对个人体育锻炼行为具有一定的影响作用。总体来说,个人体育锻炼行为受到个体受教育年限、每周工作时间、个人年收入及家庭月支出的影响。
[1] 张雷,雷雳,郭伯良. 多层线性模型应用[M]. 北京:教育科学出版社,2003:11.
[2] 汤国杰,丛湖平. 社会分层视野下城市居民体育锻炼行为及影响因素的研究[J]. 中国体育科技,2009,45(1):139-144..
[3] 熊明生,周宗奎. 锻炼行为理论的评价与展望[J].武汉体育学院学报,2009,33(4):52-58.
[4] 郭志刚,李剑钊. 农村二孩生育间隔的分层模型研究[J]. 人口研究,2006(4):28-32.
[5] 成君,赵冬,曾哲淳. 北京市居民体育锻炼现状及其影响因素分析[J]. 中国公共卫生,2007(23):5.
[6] 邱梅婷,贾绍华,陈琼霞,等. 体育锻炼习惯的形成机制和影响因素研究[J]. 首都体育学院学报,2005,17(6)28-35.
[7] 常生,天健. 影响大学生体育锻炼行为的家庭因素调查与分析[J]. 体育学刊,2008,15(3):67-70.
[8] 胡艳. 计划和障碍自我效能对锻炼意向到行为过程的解释和干预[D]. 北京:北京体育大学,2008.
[9] 张力为,毛志雄. 运动心理学[M]. 上海:华东师范大学出版社,2003.
[10] 毛荣建,晏宁,毛志雄. 国外锻炼行为理论研究综述[J]. 北京体育大学学报,2003,26(6):752-755.
[11] 吕树庭,王铮,张宏,等. 流动人口:社会体育的新课题——来自调研中的思考[J]. 广州体育学院学报,2003,23(1):1-4.
[12] 冷晓春,张册,张明记. 城市农民工体育健身的社会支持研究[J]. 南京体育学院学报:哲学社会科学版,2009,23(3):47-49.
[13] 赵燕,张永军,纪丽娥. 行为转变理论模式在社区居民体育健身锻炼行为干预中的运用[J]. 山东体育学院学报,2004,20(5):54-56.
A study of the physical exercising behaviors of urban residents in China based on a hierarchical linear model
NING Ke1,MA Yun-xia2,LI Xiao-tian3
(1.Department of Physical Education,Shanxi Institute of Education,Xi’an 710061,China;
2.School of Physical Education,Yili Normal University,Yili 835000,China;
3.Capital University of Physical Education and Sports,Beijing 100191,China)
By using some data derived from CGSS2006 urban questionnaires, and by adopting a hierarchical linear model, the authors studied the individual physical exercising behaviors of residents in urban communities in China,the drew the following conclusions: the weekly working times, educated years, individual annual incomes of individuals as independent variables in the individual hierarchy, and the monthly incomes of families as independent variables in the higher hierarchy, jointly affected the occurrence of individual physical exercising behaviors; in addition, exclusive of the influence of independent variables in the individual hierarchy, the monthly expenses of families in the family hierarchy had decisive influence on the occurrence of individual physical exercising behaviors.
social sports;physical exercising behavior;urban community;hierarchical linear model;China
G80-05
A
1006-7116(2012)02-0049-06
2011-04-26
陕西省教育厅科学计划研究项目(项目号:2010JK048)。
宁科(1979-),男,讲师,硕士,研究方向:体能训练。

