遗传算法中种群维护策略的比较

谭 阳，方 颂

(湖南网络工程职业学院，湖南长沙 410004)

遗传算法中种群维护策略的比较

谭 阳，方 颂*

(湖南网络工程职业学院，湖南长沙 410004)

遗传算法在许多优化问题中都有成功的应用，但其本身也存在一些不足。如何改善遗传算法的搜索能力，使其兼顾收敛速度和搜索范围，能更好地解决实际问题，一直是智能计算领域主要的课题之一。本文就3种常见的种群维护策略进行了比较与讨论，并分析了不同策略的优劣之处。

遗传算法;选择策略;适应度排序;欧氏距离;海明距离

一、引言

遗传算法(Genetic Algorithm ，GA)［1］是一种模拟生物进化中遗传选择和自然淘汰过程的计算模型。其算法思想源于生物遗传学和适者生存的自然规律，通过采用“生存+检测”的迭代过程进行寻优搜索。由于遗传算法具有不依赖于问题模型的特点，且还具有全局最优性、隐含并行性、高效率以及解决非线性问题稳定等特点，被广泛地应用于各个领域。尤其在数值优化领域，遗传算法以其对求解问题限制少，不要求目标函数连续可微等特性而倍受关注。但是遗传算法同样也存在局部搜索能力较差，全局优化速度缓慢，易出现早熟收敛等问题。

不失一般性，考虑如下全局优化问题:

式中，x=(x1，x2，…，xm)∈D，D⊆Rm为搜索空间，f:Rm→R 为目标函数，L=(l1，l2，…，lm)，U=(u1，u2，…，um)，［L，U］={(x1，x2，…，xm)=|li≤xi≤ui，i=1，2，…，m|}表示可行解空间，［L，U］= ⊆D，Q=D［L，U］为不可行解空间。

定义 1:向量 u=(u1，u2，…，um)称为非劣于(Dominated)向量 v=(v1，v2，…，vm)，当且仅当对于∀i∈{1，2，…，m}，ui≤vi∧∃i∈{1，2，…，m}，使得ui＜vi。

基本遗传算法中采用单点交叉算子和简单的变异算子，优点是操作简单、计算开销小，但是在使用过程存在很大的局限性［2］，由于单点交叉破坏模式的概率较小，导致搜索到的模式数目也较少，从而算法具有的搜索能力较低，难以对多维连续空间的问题进行有效搜索。

二、GA种群的维护策略

为了能保留GA在整个迭代搜索过程中偶然发现的“最优个体”，并使种群进化方向具备导向性，通常GA都会采用精英保留机制。在精英保留及指导机制的作用下会使得GA搜索效率得到很大的提高，但是带来的负面效应是对目标函数的搜索不够全面，容易使得算法陷入局部极值区，产生早熟现象，从而无法搜索到全局最优解。为此当前GA研究的重点在如何合理地维护种群的多样性。

在GA优化搜索过程中，对于种群的选择策略主要采用惩罚函数法［3］－［8］，但优化搜索的效率对惩罚函数的选择有明显的依赖性。同时，各种惩罚函数特性各异，其参数因子没有统一的选择标准，使得选择策略的取舍非常困难。若对不可行解直接采用简单的拒绝策略，种群中只保留可行解，则会大大减少搜索范围，以致GA很难收敛到最优解。通常采用的策略是:先基于某一惩罚函数的方法，选择出可行解和不可行解，并按照一定的比例或要求对可行解和不可行解进行种群混合。就国内外的研究情况而言，对于GA种群维护的策略主要可以归纳为3大类型:

1.目标函数指导

这类方法以目标函数的优化要求为基准，以筛选出种群中的最优个体为目标，并以适应度高低为评价体系对种群中所有个体以进行分级排序。某个体被筛选的依据是种群存在多少个个体优胜于该个体，并以此作为下次进化过程的选择的依据。目标函数指导方法操作简单，是一种完全按照“优胜劣汰”模式选择的策略，其典型代表为:适应度排序算法，该算法以适应度为主要关键字对种群个体进行排序，基本方法以快速排序为主，也有少量使用桶排序和计数排序［9］。

2.目标空间距离

空间距离是目前应用得较多的一种策略，也是现在研究的热点之一。该策略以某些特定个体为依据，并通过这些特定个体映射在目标函数空间之上，使之形成一些特定点(基点)其他个体也以点的形式在函数空间中投射，但其与基点的距离有特定要求，当小于某一值时则被GA舍弃。这是一种能够在相当程度维护种群多样性的策略，其特点是使某些特定点具有一定的“排异”半径，能够在多个维度上“排挤”距离过于接近的其他个体，从而使得种群以较少量的个体维持在解空间中的有效分布，其典型的代表为:欧氏(欧几里得，Euclid)距离算法，式(2)为a、b两点在空间中欧氏距离e(a，b)的计算公式［10］。

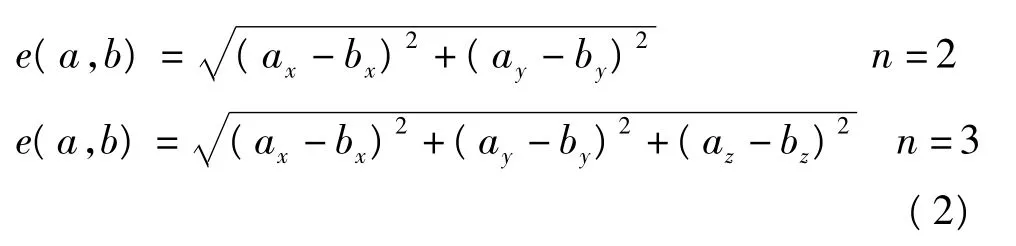
其中 x、y、z分别为 a、b 两点的坐标值，n 为 a、b两点所处空间的维度。

3.种群个体结构

此类策略应用较为少见，该策略的核心思想是以种群中个体的基因代码结构为依据来进行选择，目的是使具有类似基因结构的个体能够聚集，形成小生境环境并协同进行进化;或是以基因结构差异的大小来作为种群维护的依据。可以看出此策略和目标空间距离策略具有类似之处，前者以超平面空间为衡量依据，后者以几何空间为衡量依据。其典型的代表为:海明距离(Hamming Distance)算法，若a、b为算法种群中两个采用2进制编码的个体，那么a、b 间的海明距离 h(a，b)由下式(3)计算得出［11］。

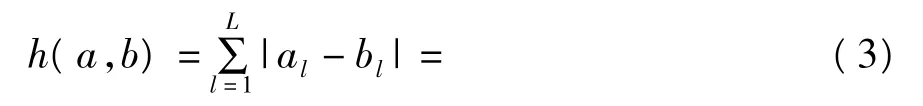
其中L为个体的2进制编码长度，l为相同位置的编码位。

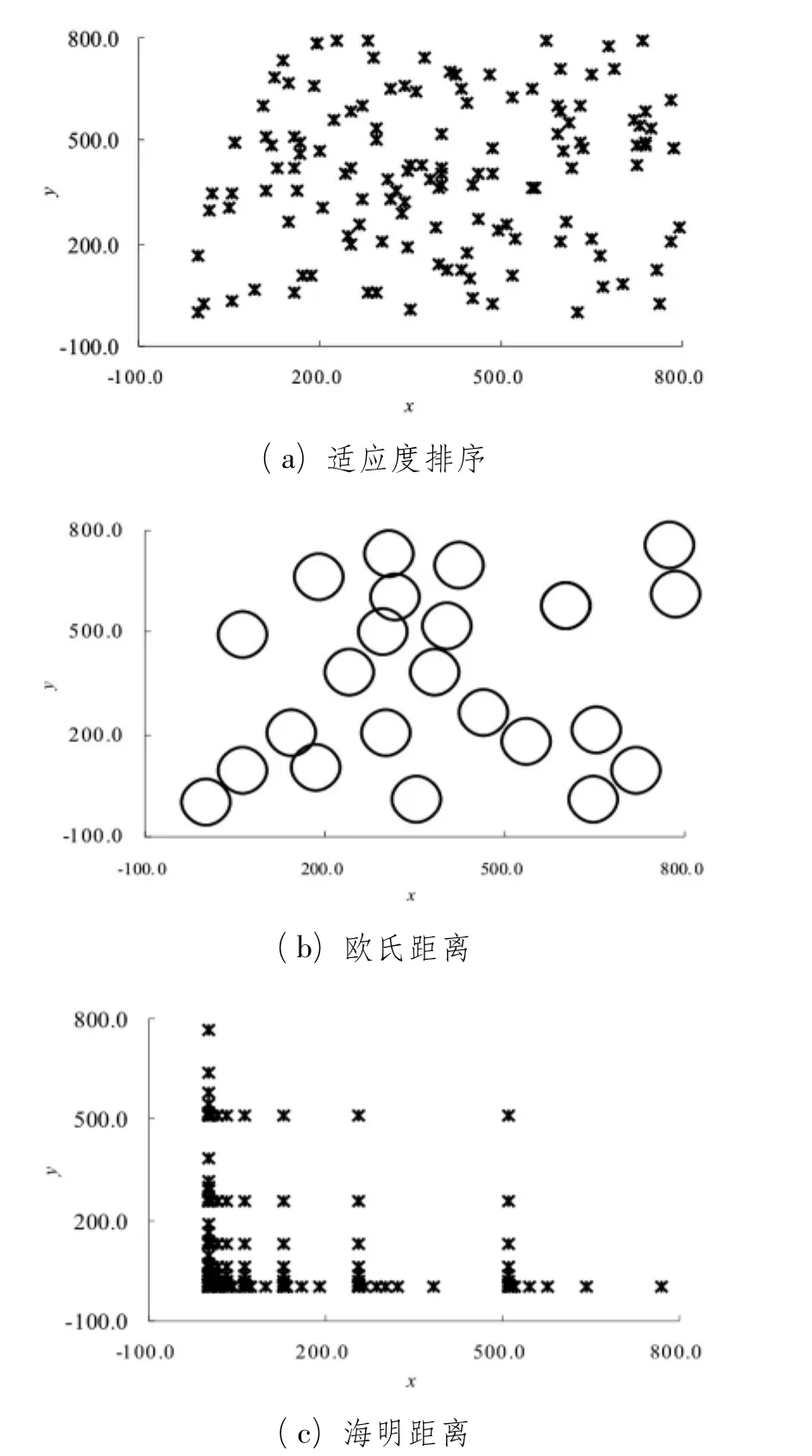
图1 3种类型的种群维护策略

图1中为3种维护策略对于基础点(0，0)在2维空间上的选择示意图。可以看出适应度排序对于搜索空间的覆盖是基于随机分布的，并以其独立个体作为指导，若需要较为有效地覆盖搜索空间则需要大量的个体进行随机尝试;但通常为了合理控制计算开销，GA在使用中会限制种群规模，这使得适应度排序策略对搜索空间的覆盖存在较大的随机性。欧氏距离策略则能够很好的解决有效覆盖需要个体过多的问题，图1(b)中可以看出只需很少量的个体即可较为有效地覆盖搜索空间，但是可行解的分布却与适应度排序一样呈现随机性和无序性。海明距离的个体分布具有明显的规律性，并呈现出“内紧外松”的分布特性，这种分布可以很好地兼顾算法搜索的效率和分布问题，但是海明距离是一种针对2进制代码的维护策略，对于采用实数编码的问题则无法运用，同时也可以看出为了保证海明距离策略的有效性，种群个体的数目远比欧氏距离策略的要高。

三、仿真测试

为了对分别采用3种维护策略的GA进行评价，本文在基本GA的基础上，建立了一个外部精英种群用于保存GA在迭代搜索过程搜索到的精英个体，并使用外部精英种群作为交叉操作的参照对象。对种群维护的策略分别采用适应度排序(Fitness－GA，FGA)、欧氏距离(Euclid －GA，EGA)和海明距离(Hamming－GA，HGA)3种方法进行维护。函数优化实验是测试迭代搜索算法性能的必备实验［12］［13］，测试所用的4个基准函数具有较强的代表性，通过寻找这些函数的最小值可以评价寻优算法的寻优性能及收敛速度，并可判断算法是否具有较好的健壮性和稳定性。

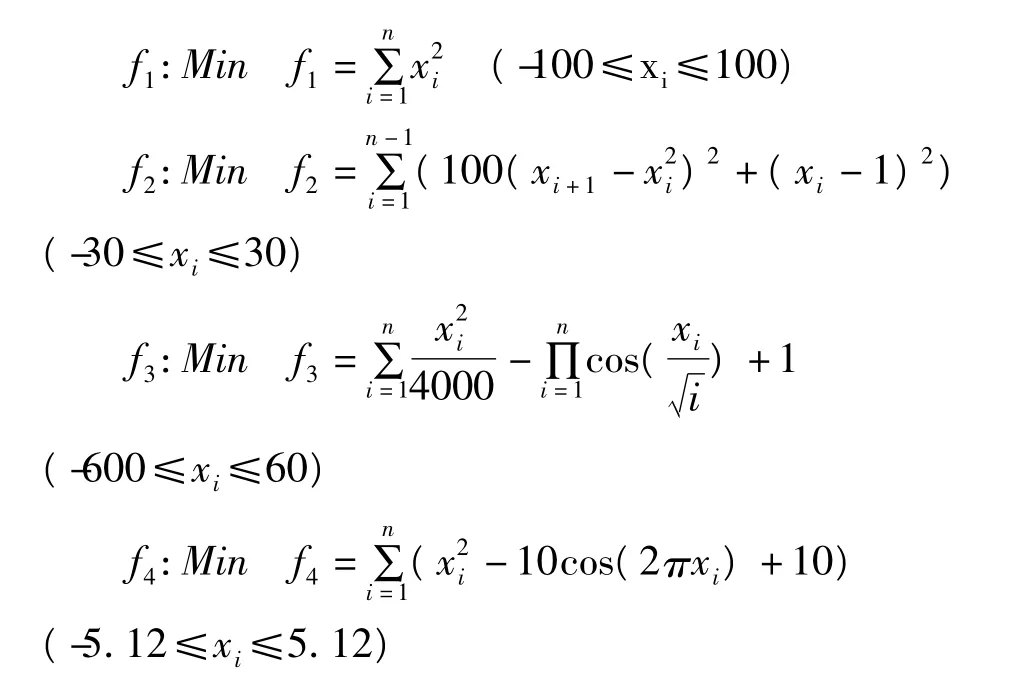
选取的测试函数f1为单峰函数;函数f2、f3和f4为多峰函数，存在多个局部极值，并且其局部最优解的个数随着维数的增加成几何级增加，这四个函数均在(0，0，…，0)处取得全局最优解。3种对比策略的给定维数分别为5维和10维，种群规模为50，最大迭代次数为500，算法的终止条件为:达到最大迭代次数或者N＞20，其中N表示连续的第Ti+1代和第Ti代种群最优值之间的差为0的次数。为了进行有效对比3种策略，对4个测试函数均使用相同的初始种群并独立按不同维数进行20次实验。

表1中为3种对比策略对函数f1～f4的测试结果，为了体现各种维护策略GA的性能，这里选取了3个指标作为对算法评价的衡量依据，分别为:平均全局最优解出现的代数，记为NGO;出现全局最优解的平均执行时间s，记为ART;平均种群最优解，记为AGO。

表1中的寻优数据表明，在对函数f1、f3和f4平均寻优结果而言HGA的结果较其他算法更为精确。对函数f2优化中HGA在平均精度上略逊于EGA，经分析f2函数为U型结构最优值呈线性分布，相对来说以“面”进行寻优的算法要好于以“点”进行寻优的算法;但是就全局最优解的平均迭代次数和平

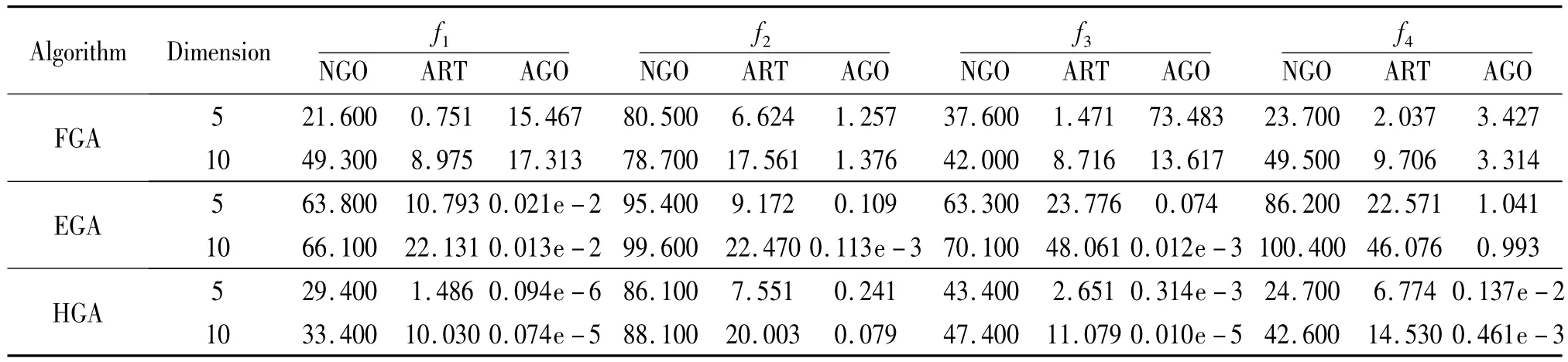
表1 对函数f1～f4优化性能的比较

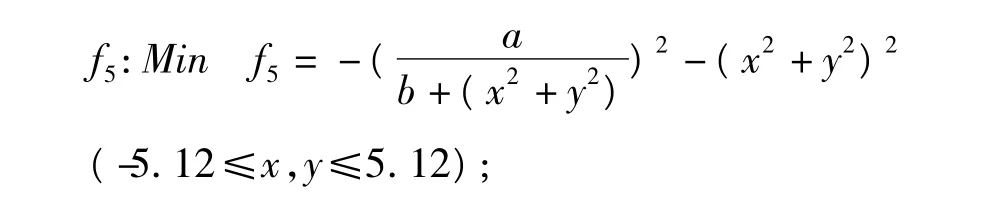
函数f5(Needle－in－a－Haystack)的参数 a，b取 a=3.0，b=0.05，该函数为典型的欺骗函数。图2(a)为该函数在MATLAB中的模拟图像，该函数的最优点分布在(0，0)处;4个局部极值点对称分布在4个角上，这些局部极值点距离全局最优点的距离很大，且函数在相当的取值范围内单调，通常优化算法难以获得全局最优解。测试中，3种对比策略的给定维数为2，种群规模为20，最大迭代次数为500，算法的终止条件为N＞20;每种算法独立运行10次并记录种群最优解。均搜索时间上FGA则领先于这两个对比策略。也可以看出FGA较为简单的维护策略并没有使得GA在迭代搜索过程中的计算开销明显增加，因此搜索速度较快。EGA则是3种策略中耗时最大的，这主要是因为需要对所有搜索的结果进行映射计算和取舍，计算量较大。

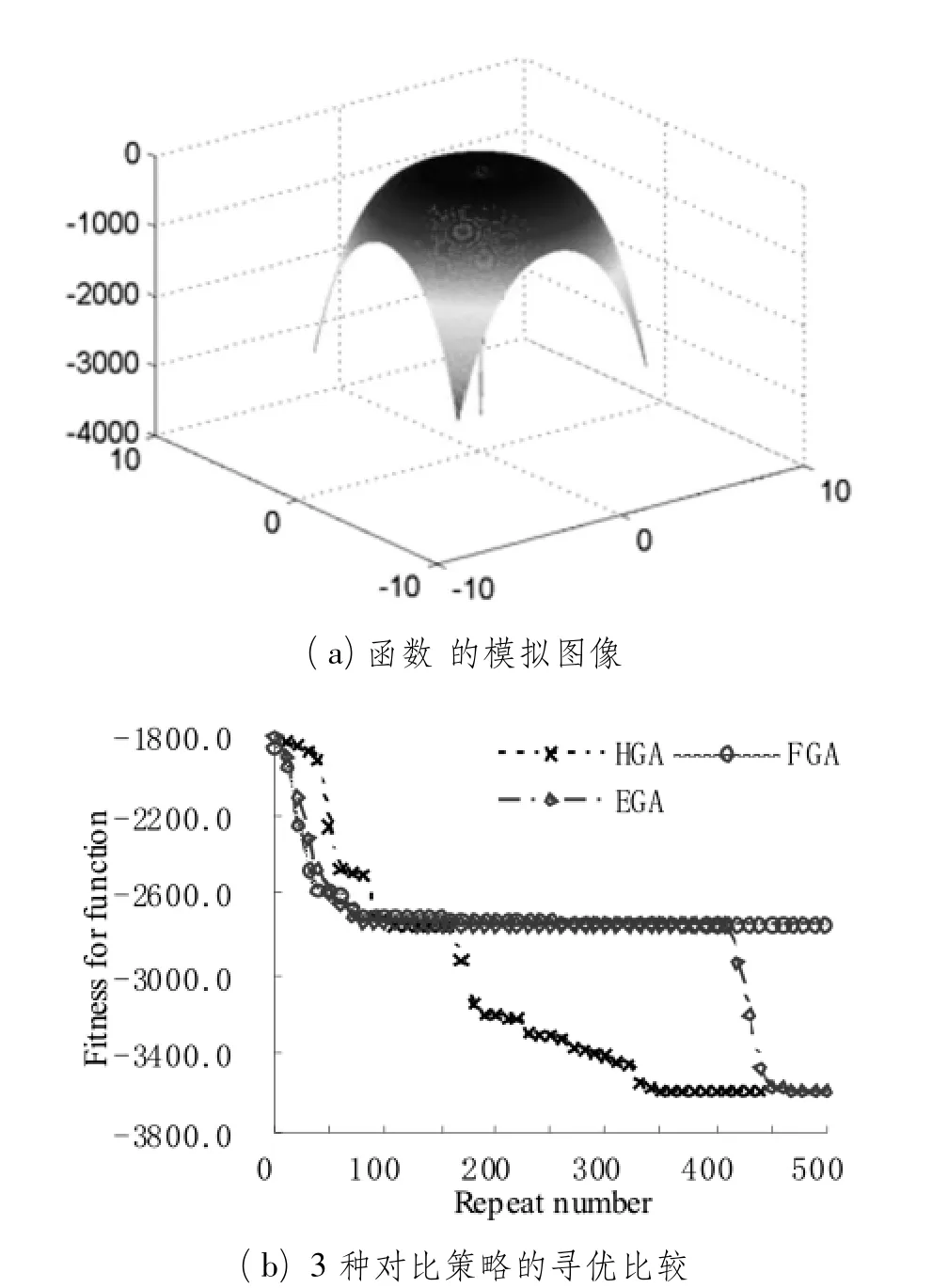
图2 对函数的优化情况

在对函数f5的优化中HGA和EGA都能搜索到全局最优解，FGA则陷入了局部极值始终未能搜索到全局最优。图2(b)反映出因为函数f5中有大范围单调区域的存在，这使得HGA和EGA都曾短暂陷入局部极值;HGA在进化到150代以后才进行了有效的收敛，EGA则进化至400代以后才进行了有效收敛，图2(b)中也可看出HGA虽然收敛的整体代数较为提前但是收敛速度却远不及EGA。就3种策略的整体情况来看HGA和EGA种群的多样性优势得以较好的体现，通过较少的迭代周期即能逃逸出局部极值的陷阱，并较快地搜寻到全局最优值，体现出较好的全局搜索能力。

四、结论

在实际运用中为了提高GA性能，通常会采用各种策略对GA的种群进行维护。本文讨论了3种类型的种群维护策略，并进行了分析和比较。本文认为对于较为简单的问题宜采用较为简单的维护策略以期获得较高计算速度;对于精度要求较高的问题则应该采用较为复杂的维护策略，相比较之下种群个体结构的策略虽然整体性能较好，但是其对于问题的通用性较差;就总体性能和使用的便利性考虑，我们推荐采用目标空间距离的策略来对GA的种群进行维护。

［1］Schraudolph N N，Belew R K.Dynamo is Parameter Encoding for Genetic Algorithms［J］.Machine learning，1992，9(1):9－21.

［2］李敏强，寇纪淞.遗传算法的模式欺骗性分析［J］.中国科学(E 辑)，2002，32(1):95 －102.

［3］李士勇，李浩.一种基于相位比较的量子遗传算法［J］.系统工程与电子技术，2010，32(10):2219－2222.

［4］Powell M.An efficient method for finding the minimum of a function of several variables without calculating derivatives［J］.Evolutionary Computation，2008，12(4):303 －307.

［5］杜海峰，公茂果，刘若辰等.自适应混沌克隆进化规划算法［J］.中国科学(E 辑)2005，35(8):817－830.

［6］Kumanan S，Jegan G，Jose K Raja.Multi－project scheduling using a heuristic and a genetic algorithm［J］.Inter J of Advanced Manu－fracturing Technology，2006，31(3－4):360－366.

［7］鲁宇明，黎明，李凌.一种具有演化规则的元胞遗传算法［J］.电子学报，2010，38(7):1603 －1607.

［8］Wei－ cai Zhong，Jing Liu，et al.A Multivalent Genetic Algorithm for Global Numerical Optimization［J］.IEEE transactions on systems，man，and cybernetics－ part B:cybernetics(S1083－4419)，2004，34(2):1128－1141.

［9］严蔚敏，吴伟民.数据结构(第2版)［M］.北京:清华大学出版社，2009:96－106.

［10］李密青，郑金华，肖桂霞，谢炯亮.基于空间距离的多目标进化算法［J］.模式识别与人工智能，2009，22(4):589～596.

［11］李敏强，寇纪淞，林丹等.遗传算法的基本理论与应用［M］.北京:科学出版社，2002:163－253.

［12］李敏强，寇纪淞，林丹等.遗传算法的基本理论与应用［M］.北京:科学出版社，2002:163－253.

［13］袁晓辉，袁艳斌，王乘等.一种新型的自适应混沌遗传算法［J］.电子学报，2006，34(4):708 －712.

A Comparison of Population Maintenance Strategies in Genetic Algorithm

TAN Yang，FANG Song

Genetic algorithms are successfully applied in many optimization procedures，but there are also some drawbacks of its own.How to improve the search capabilities of genetic algorithms to take into account the convergence speed and search range，and solve practical problems better，has been one of the main topics of intelligent computing field.In this paper，three common populations maintenance strategy are compared together，with the discussion and analysis of the strengths and weaknesses of different strategies.

Genetic algorithm(GA);selection strategy;fitness sorting;Euclidean distance;hamming distance

TP301.6

A

1009－5152(2011)04－0049－05

2011－11－18

湖南省自然科学基金项目“无线传感器网络容错技术研究”(06JJ50107);湖南省教育厅重点项目“多复变函数空间上算子理论”(10A074)。

谭阳(1979－ )，男，湖南网络工程职业学院讲师，工程师，计算数学硕士;方颂(1978－ )，男，湖南网络工程职业学院工程师。