随机电磁光束经菲涅耳波带片衍射后的传输特性
舒建华,陈子阳,蒲继雄,孙希
(1.华侨大学 信息科学与工程学院,福建 泉州 362021;2.江西警察学院 基础部,江西 南昌 330000)
随机电磁光束经菲涅耳波带片衍射后的传输特性
舒建华1,陈子阳1,蒲继雄1,孙希2
(1.华侨大学 信息科学与工程学院,福建 泉州 362021;2.江西警察学院 基础部,江西 南昌 330000)
基于相干偏振统一理论,以电磁高斯-谢尔模型光束为例,研究随机电磁光束经菲涅耳波带片衍射后的传输特性,以及入射光的相干长度、偏振度和菲涅耳波带片的最大半径数对光强和偏振度的影响.研究表明:光束的相干特性及菲涅耳波带片的最大半径数对聚焦光强会产生影响;偏振度极值的位置在焦点及次焦点附近,并且偏振度极值的位置随波带片最大半径数的变化而变化.
菲涅尔波带片;偏振;随机电磁光束;衍射;聚焦光强
自2003年美国著名光学专家Wolf提出交叉偏振统一理论[1]以来,随机电磁光束在传输过程中的光强、相干度及偏振度变化一直是研究的热点.例如,Korotkova等[2]研究了随机电磁光束在大气中传输的偏振度变化,发现当传输距离达到一定程度后,传输场中的偏振度将回复到源平面的偏振度大小,并保持不变.赵道木等[3]的研究结果表明,当满足一定条件时,完全偏振和完全非偏振的涡旋光束在传输过程中偏振度将保持不变.季小玲等[4]研究了多色部分相干电磁光束在大气湍流中传输时的偏振度变化,发现同单色光一样,多色的电磁光束经过长距离传输之后,偏振度也将最终回复到源平面的初始值.蔡阳健等[5]研究了扭曲的位相对各项同性和各项异性的电磁高斯-谢尔模型光束经像散ABCD光学系统后光束特性的影响.菲涅耳波带片是一种光束整形和聚焦的光学元件,在X射线成像、紫外成像及原子成像与聚焦等领域都有着重要的应用,因此也成为近20年的研究热点之一[6-9].对平面波经过方形的螺旋位相型菲涅耳波带片聚焦的研究表明,通过一定的调制可以获得轴上强度为零的光强分布;对平面波经过整数阶和分数阶位相型分布的菲涅耳波带片的聚焦特性的研究表明,通过调节波带片的数目和拓扑荷数可以获得并控制空心光束 .这些研究在粒子的囚禁和操控中得到了应用[10-11].此外,多色光经过菲涅耳波带片聚焦后,在相位奇点处出现相应的光谱变化[12].本文以电磁高斯-谢尔模型光束为例,研究随机电磁光束经过菲涅耳波带片之后的光束特性.
1 理论分析
菲涅耳波带片是由一系列透光和不透光圆环组成的特殊光栅,圆环的半径满足
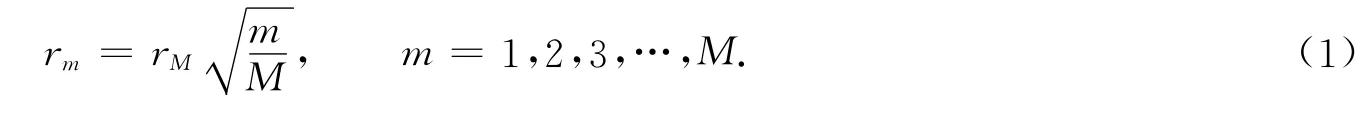
式(1)中:M为菲涅耳波带片的最大半径数;rM为菲涅耳波带片的最大半径.当M为奇数时,波带片的中心部分是一圆孔,完全透光;当M为偶数时,波带片的中心部分是一圆屏,完全不透光 .光束通过菲涅尔波带片的衍射示意图,如图1所示.
一束沿z方向的电磁波,在菲涅耳波带片所在的平面(z=0)的交叉谱密度矩阵[1]可表示为
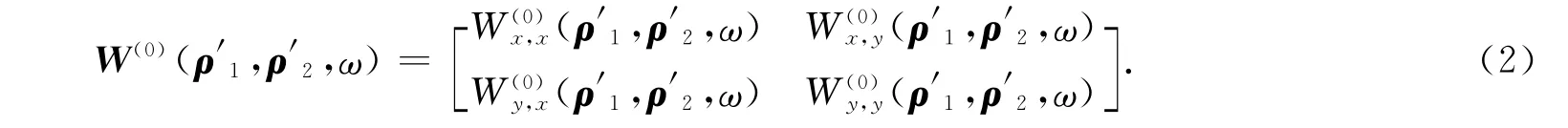
以高斯-谢尔模型光束为例,研究随机电磁光束经菲涅耳波带片的衍射特性,简单起见,假设其交叉项为零,因此各矩阵元可表示为
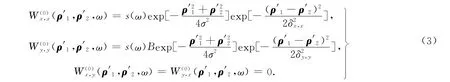
为了书写方便,将式(2)合写成一个方程,即
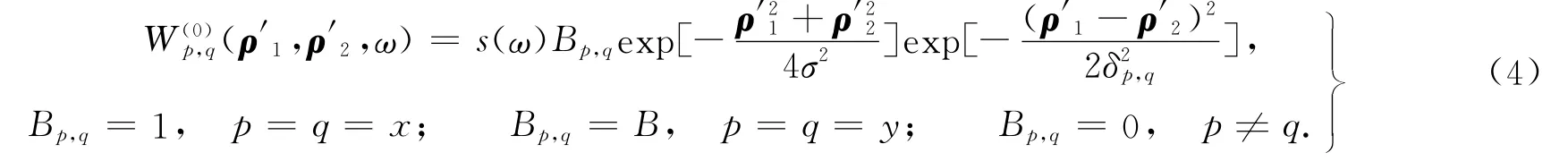
式(4)中:ρ′1和ρ′2是z=0平面内的位置矢量,均与z轴垂直;s(ω)表示原点处的谱密度;参数B,σ,δx,x和δy,y均与位置无关,但可能与频率ω有关.
电磁波束的偏振度由一般的文献[1]的公式给出,即

将式(2),(3)代入式(5)后,可得到在菲涅耳波带片处的电磁波束的偏振度,即

高斯-谢尔模型光束在观察平面z内(ρ1,ρ2)两点的交叉谱密度矩阵元[13]为
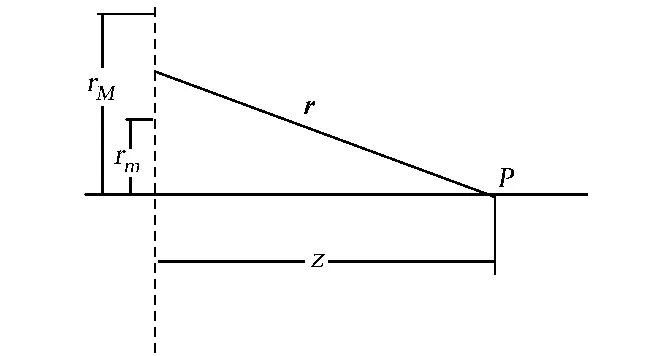
图1 光束通过菲涅尔波带片的衍射示意图Fig.1 Scheme of the light diffracted by Fresnel zone plates
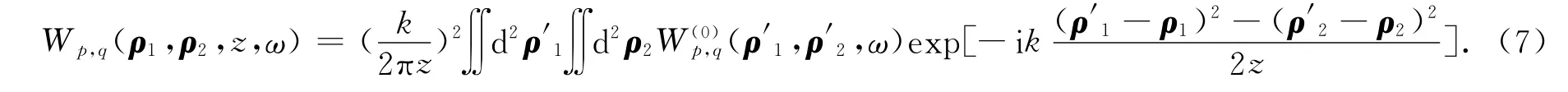
将式(4)代入式(7),可得到
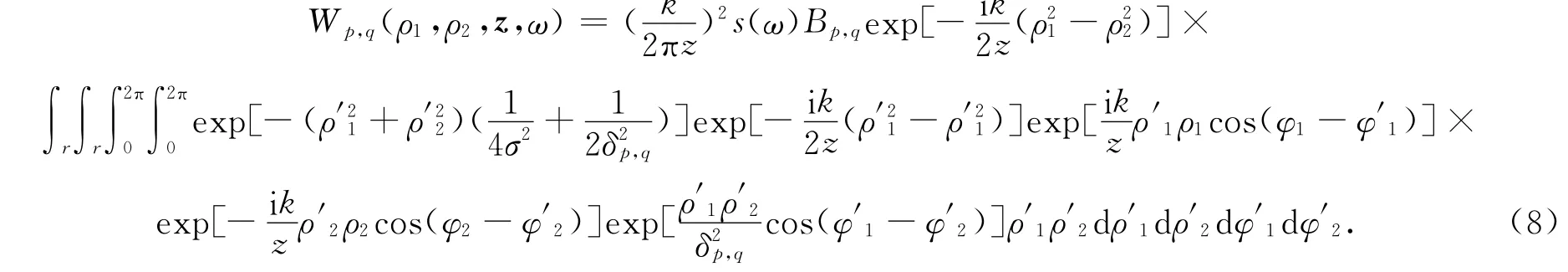
根据文献[14],有
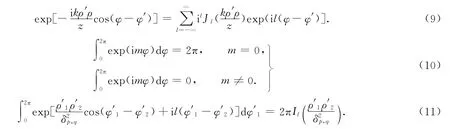
双圆环菲涅耳波带片(M=4)的积分区间在[r1,r2]和[r3,r4],可得到z平面内两点(ρ1,ρ2)的交叉谱密度矩阵元的解析表达式为
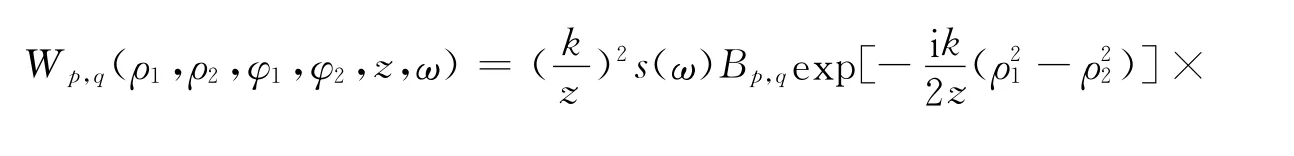
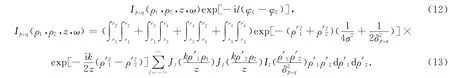
令ρ1=ρ2=ρ,φ1=φ2=φ,可得到高斯-谢尔模型光束通过双圆环菲涅耳波带片后,其交叉谱密度的各矩阵元为
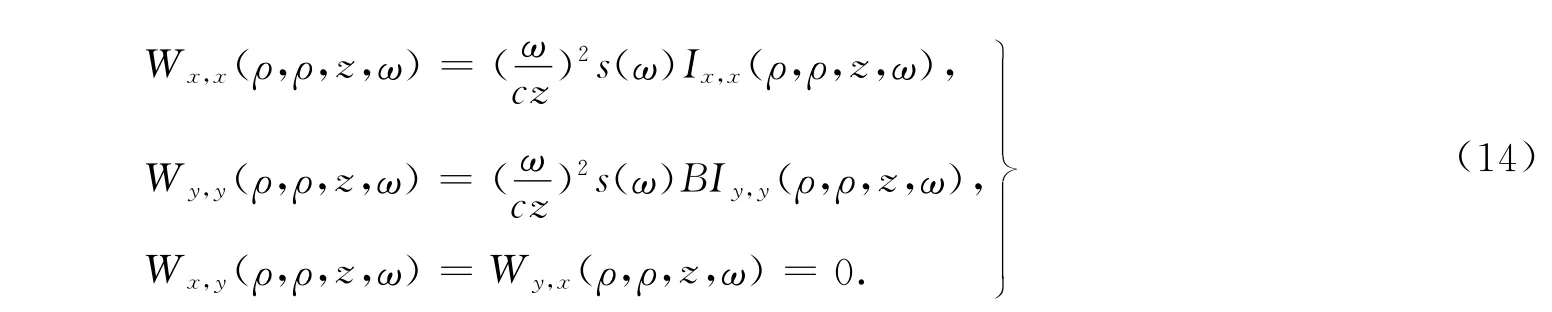
高斯-谢尔模型光束通过双圆环菲涅耳波带片后,其在点(ρ,φ,z)的光强和偏振度[1]分别为
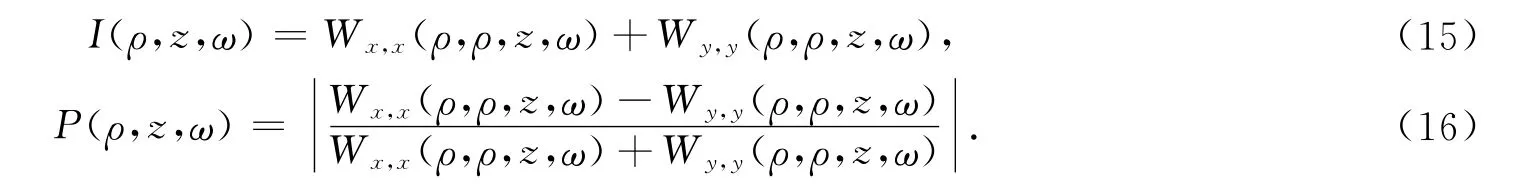
2 数值模拟
基于式(15),(16),对高斯-谢尔模型光束经过菲涅耳波带片后的光强和偏振度进行数值模拟.不同相干长度的部分相干高斯-谢尔模型光束经菲涅耳波带之后,其光强分布情况如图2所示.图2中:λ=632.8nm,σ=1mm,r1=0.67mm,P0=0,M=6.

图2 相干长度对光强分布的影响Fig.2 Influence of the correlation length on the distribution of light intensity
随机电磁光束经不同最大半径数(M)的菲涅耳波带片衍射后,其光强分布情况如图3所示.图3中:δx,x=δy,y=1mm,其他参量与图2相同.从图3可以看出:随着最大半径数的增加,焦点处的轴上光强分布更加集中,所获得聚焦焦斑将变小.
以6个环的菲涅耳波带片为例,研究相干长度对轴上点偏振度的影响,如图4所示.图4中:δx,x=1 mm;P0=0.5;其他参量与图2相同;所取的源平面偏振度为0.5(B=1/3),即y方向的光强为x方向的1/3.从图4可以发现:当δx,x=δy,y时,即两个方向的相干特性相同时,衍射场中轴上点的偏振度将保持和入射光的偏振度相同;当δx,x>δy,y时,在焦点处和1/3焦点处附近的偏振度数值最大;而当δx,x<δy,y时,在焦点处和1/3焦点处附近的偏振度数值最小.
究其原因,当δx,x=δy,y时,x方向和y方向的聚焦特性相同,所以偏振度和入射光偏振度相同;当δx,x>δy,y时,从图2中的结论可知,相比于入射光x方向光强与y方向光强的比值,聚焦点x方向的聚焦光强与y方向光强比值将更大,因而偏振度较大;而当δx,x<δy,y时,相比于入射光x方向光强与y方向光强的比值,聚焦点x方向的聚焦光强与y方向光强比值将减小,使得焦点处的偏振度变小.
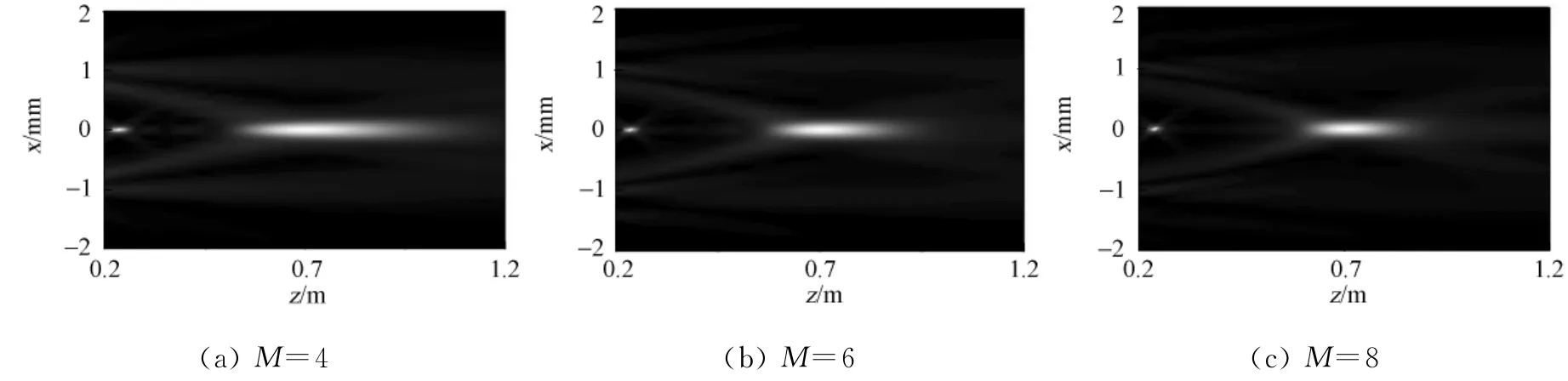
图3 菲涅耳波带片的最大半径数对聚焦衍射光强的影响Fig.3 Influence of the max radius number of zone plates on the distribution of focusing light intensity
入射光偏振度对衍射场轴上点偏振度的影响,如图5所示.图5中:δx,x=1mm,δy,y=0.5mm,其他参量与图2相同.从图5可以看出:当入射光的偏振度越大,则衍射后轴上点的偏振度也越大.当入射光的偏振度为1时,轴上点的偏振度也始终为1.这是因为入射光偏振度为1时,B的取值为0,即入射光仅仅只有x方向的分量,没有y方向的分量 .因此,在传输过程中始终只有x方向分量的光强,从而偏振度为1.
以最大半径数(M)为4,8,12的菲涅耳波带片为例,研究菲涅耳波带片的最大半径数对轴上点偏振度的影响,如图6所示.图6中:δx,x=1mm,δy,y=0.5mm,其他参量与图2相同.从图6可知:对于所选取的参量,当菲涅耳波带片的最大半径数比较少时,轴上点的偏振度的极大值和极小值也较小;随着波带数的增加,轴上点偏振度的极大值和极小值将变大.此外,随着最大半径数的增加,焦点附近的偏振度极大值的位置越靠近焦点.
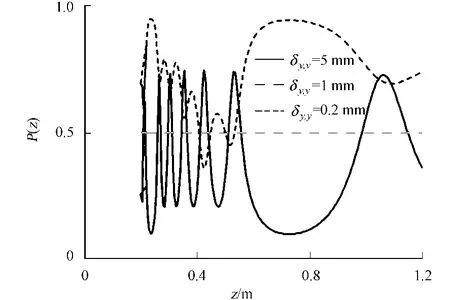
图4 相干特性对轴上点偏振度的影响.Fig.4 Influence of the coherence on the degree of polarization for on-axial points
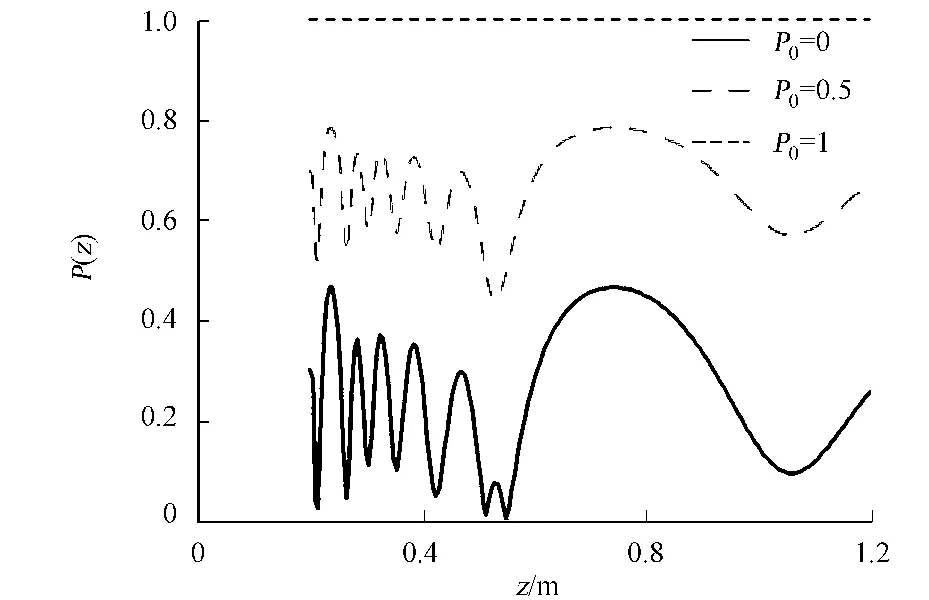
图5 入射光偏振度对轴上点偏振度的影响Fig.5 Influence of the degree of polarization of the incident light on the degree of polarization for on-axial points
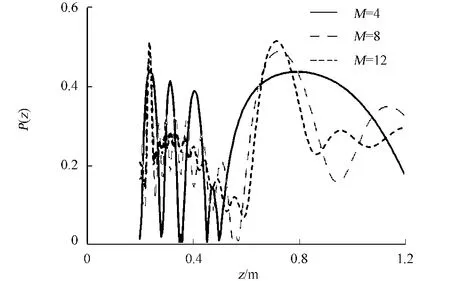
图6 菲涅耳波带片的最大半径数对轴上点偏振度的影响Fig.6 Influence of the max radius number of Fresnel zone plates on the degree of polarization for on-axial points
3 结论
以电磁高斯-谢尔模型光束为例,基于交叉偏振统一理论和交叉谱密度传输公式,研究随机电磁光束经过菲涅耳波带片后在衍射场中的光强及偏振度分布,得到如下4点结论.
(1)光强和偏振度分布随着入射光的相干度、偏振度,以及波带片的最大半径数的变化而变化.
(2)光束经菲涅耳波带片后,在衍射场中的焦点处和1/3焦点处将出现聚焦光斑.
(3)入射光的相干度越高、菲涅耳波带片的最大半径数越多,所获得的聚焦光斑越小.
(4)偏振度的极值将出现在焦点处附近,极值的大小与入射光的偏振度和相干度有关,极值的位置和菲涅耳波带片的最大半径数有关.随着最大半径数的增加,极值的位置更加靠近焦点.
[1]WOLF E.Unified theory of coherence and polarization of statistical electromagnetic beams[J].Phys Lett(A),2003,312:263-267.
[2]KOROTKOVA O,SALEM M,WOLF E.The far-zone behavior of the degree of polarization of electromagnetic beams propagating through atmospheric turbulence[J].Opt Commun,2004,233(4/5/6):225-230.
[3]DU Xin-yue,ZHAO Dao-mu.Criterion for keeping completely unpolarized or completely polarized stochastic electromagnetic Gaussian Schell-model beams on propagation[J].Opt Express,2008,16(20):16172-16180.
[4]JI Xiao-ling,ZHANG En-tao,LÜBai-da.Changes in the spectrum and polarization of polychromaticially coherent electromagnetic beams in the turbulent atmosphere[J].Opt Commun,2007,275(2):292-300.
[5]CAI Y J,KOROTKOVA O.Twist phase-induced polarization changes in electromagnetic Gaussian Schell-model beams[J].Appl Phys B,2009,96(2/3):499-507.
[6]WILHEIN T,KAULICH B,FABRIZIO E D,et al.Differential interference contrast X-ray microscopy with submicron resolution[J].Appl Phys Lett,2001,78(14):2082-2084.
[7]CAMNAL O,SIGEL M,SLEATOR T,et al.Imaging and focusing of atoms by a fresnel zone plate[J].Phys Rev Lett,1991,67(23):3231-3234.
[8]DOAK R B,GRISENTI R E,REHBEIN S,et al.Towards realization of an atomic de broglie microscope:Helium atom focusing using fresnel zone plates[J].Phys Rev Lett,1999,83(21):4229-4232.
[9]ZHANG Bin-zhi,ZHAO Dao-mu,WANG Shao-min.Demonstrations of the diffraction and dispersion phenomena of part Fresnel phase zone plates[J].Appl Phys Lett,2007,91(2):021108.1-021108.3.
[10]ZHANG Bin-zhi,ZHAO Dao-mu.Focusing properties of Fresnel zone plates with spiral phase[J].Opt Express,2010,18(12):12818-12823.
[11]ZHANG Bin-zhi,ZHAO Dao-mu.Square fresnel zone plate with spiral phase for generating zero axial irradiance[J].Opt Express,2010,35(9):1488-1490.
[12]渠彪,蒲继雄.菲涅耳波带片衍射产生的光谱奇异现象[J].华侨大学学报:自然科学版,2007,28(1):46-50.
[13]MANDEL L,WOLF E.Optical coherence and quantum optics[M].New York:Cambridge University Press,1995.
[14]GRADSJTEUM I S,RYZHIK I M.Table of integrals,series,and products[M].New York:Academic Press,1980.
Transmission Properties of Stochastic Electromagnetic Beams Diffracted by Fresnel Zone Plates
SHU Jian-hua1,CHEN Zi-yang1,PU Ji-xiong1,SUN Xi2
(1.College of Information Science and Engineering,Huaqiao University,Quanzhou 362021,China;2.Basic Course Department,Jiangxi Public Security College,Nanchang 330000,China)
Based on the unified theory of coherence and polarization,Electromagnetic Gaussian Schell-model beam was taken as an example to study the transmission properties of random electromagnetic beams diffracted by Fresnel zone plates,the influence of correlation length,the degree of polarization of incident light,and the max radius number of zone plates on the light intensity and the degree of polarization.It is shown that the coherent property and the max radius number of zone plates will influence the focusing intensity,that the position of extremum of degree of polarization is near by the focus and the second focus,and it varies with the change of the max radius number of zone plates.
Fresnel zone plates;polarization;stochastic electromagnetic beams;diffraction;focusing intensity
钱筠 英文审校:吴逢铁 )
O 436.1
A
1000-5013(2011)06-0618-05
2010-10-06
舒建华(1955-),男,副教授,主要从事光的传输和量子光学的研究.E-mail:sjh@hqu.edu.cn.
国家自然科学资金资助项目(60977068);中国科学院西安光学精密机械研究所瞬态光学与光子技术国家重点实验室开放基金资助项目(SKLST200912);国务院侨办科研基金资助项目(10QZR01)

