响应面法在试验设计与优化中的应用

张泽志，韩春亮，李成未

(河南教育学院化学系，河南郑州 450046)

响应面法在试验设计与优化中的应用

张泽志，韩春亮，李成未

(河南教育学院化学系，河南郑州 450046)

简要介绍了响应面法，并结合实例介绍了响应面法所用数据处理软件Design Expert在试验设计与优化中的应用.

响应面法;Design Expert;软件;数据处理;优化

响应面法(Response Surface Method，RSM)，也称响应曲面法，是通过对响应曲面及等高线的分析寻求最优工艺参数，采用多元二次回归方程来拟合响应值与因素之间函数关系的一种优化统计方法［1－2］.该方法将试验体系的目标响应值(如植物活性成分的提取率)作为单个或多个试验因素(如提取时间、溶剂浓度等)的函数，并将这种函数关系通过多维图形显示出来，试验者利用图形分析、函数求导等手段优化试验设计中的最佳条件.响应面法一般包括以下主要步骤:试验设计、构建模型、检验模型、优化最佳组合条件和验证最佳组合条件等.利用响应面法拟合的回归方程模型和绘制的响应曲面及等高线，可以求出各试验因素相应水平的响应值，在此基础上优化最优响应值以及最佳试验条件.因此，必须通过大量试验数据构建一个合适的数学模型(即建模)表示和分析响应面以寻找最优区域或确定最佳优化条件.若模型中只有一个试验因素或自变量，响应曲面为二维空间中的一条曲线;若有两个试验因素或自变量时，响应曲面则为三维空间中的曲面.

响应面法的优点是在试验条件优化过程中可以连续地对试验因素的各个水平进行分析，克服了正交试验只能对一个个孤立的试验点进行分析和不能给出直观图形的缺陷，所以响应面法被广泛应用于试验设计与工艺优化研究［3－6］.响应面法最常用的软件为Design Expert 8.0系列，可在STATEASE官方网站［7］下载.下面以文献［3］为例，简单介绍响应面法及Design Expert软件的应用.

1 试验因素的选取和单因素最优取值点确定

根据相关文献和初步试验，确定影响芹菜总黄酮得率的试验因素和水平.本试验选择提取溶剂、微波提取时间、微波功率、液固比等因素.首先作单因素试验以确定各因素的最优取值点，如文献［3］中微波提取时间为8 min、微波功率为500 W、液固比为30∶1 mL·g－1.

2 响应面试验设计

确定响应面试验设计因素和水平的方法有多种，经常使用的方法有:利用已有相关文献结果、利用单因素试验［5］、利用爬坡试验［8］、利用两水平因子设计试验［9－10］等.文献［3］通过单因素试验确定响应面试验设计的因素和水平.采用软件中Box-Benhnken Design设计试验方案，以各试验单因素最优取值点为中心，上下区域各取1个水平值(若取2个水平值，则试验设计多采用Central Composite Design设计)作为响应面试验设计水平，即微波提取时间为6 min、8 min、10 min，微波功率为450 W、500 W、550W，液固比为20∶1 mL·g－1、30∶1 mL·g－1、40∶1 mL·g－1(见文献［3］中表1).将各因素及其水平值依次输入系统，则生成如文献［3］中表2所示的试验方案，按照该方案进行试验，记录每组因素组合的试验结果，并将试验结果填入对应Response列，即黄酮得率，如图1所示.

3 构建数学模型及检验模型

点击Analysis下的黄酮得率(Analyzed)按钮，即显示如图2所示窗口.依次点击各按钮会出现相应的分析结果，如点击f(x)Model会出现影响二次方程模型的常数项、一次项、二次项(包括交互作用项)等，如图2所示.数学模型的构建及其方差分析、方程的显著性检验、系数显著性检验可通过ANOVA按钮显示，如图3、图4所示.采用多元二次回归方程拟合整理后可得到文献［3］中的式(2)和方差分析表(表3).文献［3］对微波辅助提取芹菜总黄酮试验的数学模型进行方差分析，以检验由响应面拟合所得二次方程的适用性，并通过比较各因素回归系数的大小来确定各因素对芹菜总黄酮得率的影响程度.分析结果表明，一次项中微波功率X1(图4中A)和提取时间X2(图4中B)的F值(F-Value)较大且Prob＞F的值小于0.000 1，说明微波功率和提取时间对芹菜总黄酮得率的影响极为显著;因素间交互作用对黄酮得率的影响中，交互项X1X2(即AB)的偏回归系数最小，说明微波功率和提取时间之交互项对黄酮得率的影响极为显著.方差分析结果(模型的Prob＞F项目值小于0.000 1)表明，该方程模型极显著(significant).而失拟项(Lack of Fit)检验为不显著(not significant)，说明该方程对试验拟合较好.

图1 试验分析方案及结果Fig.1 Experiment arrangement and results

图2 影响二次方程模型的因素Fig.2 The influence factors of quadratic equation model

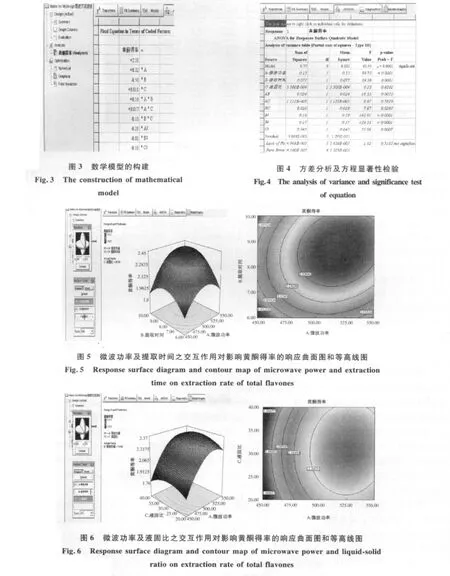
采用多元二次回归方程拟合图1中的试验数据，分析此方程所代表的响应曲面，可推算出试验因素在响应曲面中所覆盖的区域并初步筛选因素的最佳取值范围.根据二次方程模型分别做出试验因素间交互作用的3-D响应曲面和等高线(见图5和图6)，以考察微波功率及提取时间和微波功率及液固比的交互作用对芹菜黄酮得率的影响.

由图5可以看出，若固定液固比不变，微波功率及提取时间之交互作用对黄酮得率的影响显著，黄酮得率随微波功率及提取时间的增加而呈现由低到高再降低的趋势，即黄酮得率在合适的微波功率及提取时间下具有极大值，该极大值存在于响应曲面的顶部，可通过计算或分析等高线而得到.

由图6可知，固定提取时间，在一定范围内黄酮得率随微波功率及液固比的增加呈现由低到高再降低的趋势，即黄酮得率在合适的微波功率及液固比条件下具有极大值，该极大值存在于响应曲面的顶部，同样可通过计算或分析等高线而得到.

4 优化最佳组合条件

通过上述分析可知，合适的微波功率、提取时间和液固比等试验因素水平有利于芹菜总黄酮的提取，因此可以采用软件优化功能，或者利用二次方程模型分别对参数Xi求导，联解求导所得的方程，即可得到最佳试验条件.文献［3］采用软件Optimization的Numerical优化功能，在试验因素取值范围内(in rang)选择最低点为出发点，响应值选取最大值(maximum)，可优化得到微波辅助提取芹菜总黄酮的理论最佳条件:即微波功率为520.31 W，提取时间为8.65 min，液固比为32.59∶1 mL·g－1，该条件下芹菜总黄酮得率的预测值为2.449 mg·g－1.

5 验证最佳条件

为检验响应面法的可靠性，一般需对优化所得理论最佳条件进行验证.考虑到试验操作的便利和可控性，文献［3］采用上述优化条件进行微波提取芹菜总黄酮验证试验时，将提取工艺条件调整为微波功率为520 W，提取时间为9 min，液固比为32∶1 mL·g－1，平行做5次验证试验，测得芹菜总黄酮的平均得率为2.443 mg·g－1，该值与理论预测值2.449 mg·g－1相比，其相对误差很小(约为0.02%).由此可见，基于响应面法所得微波提取芹菜总黄酮的方程模型适用性强、优化试验工艺条件准确可靠，具有一定的应用价值.

［1］ BOX G E P.Statistics for Experiments:An Introduction to Design，Data Analysis and Model Building［M］.New York:Wiley，1990.

［2］ MONTGOMERY D C.实验设计与分析［M］.傅钰生，张健，王振羽，等，译.6版.北京:人民邮电出版社，2009:366－379.

［3］ 张泽志，王福安，高霞，等.响应面法优化微波提取芹菜总黄酮工艺的研究［J］.郑州大学学报:工学版，2010，31(6):95－99.

［4］ 高配科，马挺，赵玲侠，等.胜利油田沾3区块内源微生物激活剂的筛选、优化及效果评价［J］.化工学报，2011(7):2005－2012.

［5］ 张泽志，高霞，林钰，等.用响应面法优化微波提取花生壳总黄酮工艺［J］.河南工业大学学报:自然科学版，2010，31(4):32－36.

［6］ 陈晓惠，杜建修.金纳米粒子催化鲁米诺—异烟肼化学发光反应及其分析应用［J］.化学学报，2011(6):745－751.

［7］ State-Ease Inc.Down load the Design-Expert 8.0 Trial Program［EB/OL］.［2011－05－08］.http://www.statease.com/dx8trial.html.

［8］ 顾艳丽，张慧，刘赛男，等.响应面优化产碱性蛋白酶菌株的产酶条件［J］.大连工业大学学报，2011(1):5－9.

［9］ 欧祖军.部分因析设计的最优折叠反转及相关问题的研究［D］.武汉:华中师范大学，2011.

［10］顾骏，叶蕊芳，郑黎.他克莫司发酵培养基的响应面优化设计［J］.工业微生物，2008(2):60－63.

Application of Response Surface Method in Experimental Design and Optimization

ZHANG Ze-zhi，HAN Chun-liang，LI Cheng-wei

(Department of Chemistry，Henan Institute of Education，Zhengzhou450046，China)

Response surface method and its application were introduced briefly through a case in which the data processing software Design Expert was used in experiment design and optimization.

response surface method;Design Expert;software;data processing;optimization

TB11;O652

A

1007－0834(2011)04－0034－04

10.3969/j.issn.1007－0834.2011.04.012

2011－09－23

河南省科技攻关项目(092102310348)

张泽志(1971—)，男，河南柘城人，河南教育学院化学系讲师.