基于非交换代数结构的公钥密码体制

李绍华，尚绪凤

(中国计量学院理学院，浙江杭州 310018)

基于非交换代数结构的公钥密码体制

李绍华，尚绪凤

(中国计量学院理学院，浙江杭州 310018)

提出了一个新的基于非交换代数结构的Diffie－Hellman密钥交换协议，并在此基础上建立了一个新的公钥密码体制.它的安全性取决于一个基本问题的困难性，而这个基本问题是共轭搜索问题和Diffie－Hellman问题的结合变形问题.最后将提出的体制应用到数字签名方案中，并给出一个类似于ElGamal的签名方案.

非交换代数结构;Diffie－Hellman密钥交换协议;扭共轭搜索问题;公钥密码体制

0 引言

随着密码技术的发展，非交换代数结构已成为构造密码体制的一个趋势，也引起了学者们的广泛关注.许多优秀的以非交换结构为平台的密码体制相继提出［1－2］，例如辫群就是一个很好也很重要的平台.非交换结构中常见的问题是共轭搜索问题和Diffie－Hellman问题.本文将提出一个基本问题，它是共轭搜索问题和Diffie－Hellman问题的结合问题，本文提出的方案就是基于该基本问题，并且适用于一般的非交换结构.文献［1］也提出了一个类似的问题，但是是以辫群为指定的平台进行讨论的.

共轭搜索问题:已知x，y∈G，且x与y互为共轭的，找出a∈G，s.t:y=axa－1.共轭搜索问题还有一个推广，即扭共轭搜索问题［3］:已知x，y∈G，φ，ψ∈End( G)，*为G上的反同态，找出a∈G，s.t:y=ψ(a) xφ( a*).这一问题比一般的共轭搜索问题更为不平凡，并且更适合于构造复杂的密码体制.再给出DH问题:已知g，gkA，gkB∈F，计算gkAkB.Diffie－Hellman问题也有一个推广的问题，即:令φ，ψ∈Aut( G)，且φψ=ψφ，已知a，φ(a)，ψ(a)，求φ( ψ(a)).本文使用的基本问题:设G是非交换的代数结构，已知x∈G且x∉Z( G)，φ，ψ是G到Z( G)上的同态，*为G上的反同态，y1=ψ(a) xφ( a*)，y2=ψ(b) xφ( b*)，a，b∈G是隐藏的，计算ψ(a) y2φ( a*)或ψ(b) y1φ( b*).此问题可以看成共轭搜索问题和Diffie－Hellman问题的一个变形，它显然比一般的共轭搜索问题和Diffie－Hellman问题更难解决.一般的共轭搜索问题存在所谓的“基于长度的攻击”，一些试探性的算法已经显示出非常高的成功率［4－7］.而考虑我们所提出的基本问题时，线性攻击似乎是不可行的，见文献［3］中的具体分析.

注:在非交换结构中，ψ(a) y2φ( a*)不一定等于ψ(b) y1φ( b*)，而由于φ，ψ是G到Z( G)上的同态，故两者是相等的.这是共轭问题应用到Diffie－Hellman密钥交换协议的关键问题，文献［1］中是利用辫群的自身结构来解决这一问题的，而本文通过同态的选取可将方案推广到一般的非交换结构中.

1 提出的方案

1.1 非交换群上的Diffie－Hellman密钥交换协议

假设Alice想与Bob达成一个会话密钥，G是非交换群，公开信息为x∈G－Z(G)，φ，ψ:G→Z( G)，G上的反同态*，协议如下

(1)Alice选取随机元a∈G，计算y1=ψ(a) xφ( a*)，并将y1发给Bob;

(2)Bob选取随机元b∈G，计算y2=ψ(b) xφ( b*)，并将y2发给Alice;

(3)Alice和Bob分别计算KA=ψ(a) y2φ( a*)和KB=ψ(b) y1φ( b*).

由于

故达成的会话密钥为K=KA=KB.

1.2 非交换群上的公钥密码体制

利用上面的协议，建立一个新的公钥密码体制.令G为非交换群，H:G→{0，1}k是一个适当选取的杂凑函数.

(1)密钥生成系统选择x∈G－Z( G)，两同态φ，ψ:G→Z( G)，和G上的一个反同态*.A选择随机元a∈G，计算y= ψ(a) xφ( a*)，则A的公钥为(x，y)，私钥为a.

(2)加密给定消息m∈{0，1}k，假设B要将m发给A，则B选择随机元b∈G，利用A的公钥计算c=ψ(b) xφ( b*)，d= H( ψ(b) yφ( b*))⊕m，密文为(c，d).

(3)解密A收到密文(c，d)，利用私钥解密得m=H( ψ(a) cφ( a*))⊕d.

以上体制是正确的，因为

2 应用

上一节提出的公钥密码体制可以用于构造各种数字签名方案.下面给出一个类似于ElGamal的签名方案.

设G为非交换群，x∈G－Z( G)，两同态φ，ψ:G→Z( G)，反同态设为元素的逆运算.假设用户要为消息m签名.

(1)选择随机元a∈G，计算y=ψ(a) xφ( a*);

(2)选择随机元k∈G，计算r=ψ( k－1)xφ(k)，z=ψ( r－1)yφ(r);

(3)计算δ，s.t:m=δk(ar)－1.

最后得到的签名为(m，z，δk).这里a可以看做签名人的私钥，公钥为y，保密信息为(a，k，r，δ).

接收者收到签名后，计算L=ψ(m) xφ( m－1)，R=ψ( δk) zφ((δk)－1)，当且仅当L=R时接受签名.

此签名方案是正确的，因为

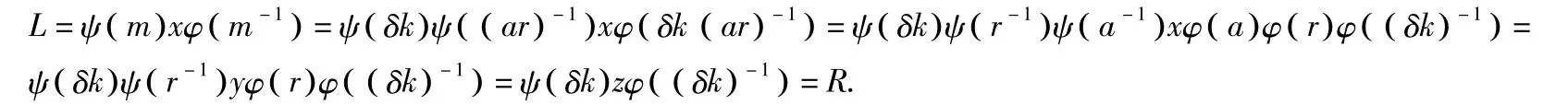
3 结束语

本文将一般的共轭搜索问题与Diffie－Hellman问题相结合提出了一个基本问题，这个问题的困难性不低于共轭搜索问题和Diffie－Hellman问题.在此基础上提出了新的Diffie－Hellman密钥交换协议和新的公钥密码体制，并且提出了一个数字签名方案.我们的体制比一般的基于共轭搜索问题或Diffie－Hellman问题的方案更有优势.一方面是提出的基本问题能更好地抵抗线性攻击，另一方面我们的方案对一般的非交换结构都是适用的，更具有普遍性.

［1］KO K H，LEE S J，CHEON J H.New public key cryptosystem using braid groups［J］.Lecture Notes in Computer Science，2000，30(1880): 166－183.

［2］PAENG S H，HA K C，KIM J H，et al.New public key cryptosystem using finite non Abelian groups［J］.Lecture Notes in Computer Science，2001，31(2139):470－485.

［3］SHPILRAIN V，USHAKOV A.An authentication scheme based on the twisted conjugacy problem［J］.Lecture Notes in Computer Science，2008，38(5037):366－372.

［4］GARBER D，KAPLAN S，TEICHER M，et al.Probabilistic solutions of equations in the Braid group［J］.Advances in Applied Mathematics，2005，35(3):323－334.

［5］GARBER D，KAPLAN S，TEICHER M，et al.Length-based conjugacy search in the Braid group［J］.Contemp Math Amer Math Soc，2006，54 (418):75－87.

［6］MYASNIKOV A D，USHAKOV A.Length based attack in braid groups［J］.Lecture Notes in Computer Science，2007，37(4450):76－88.

［7］RUINSKIY D，SHAMIR A，TSABAN B.Cryptanalysis of group-based key agreement protocols using subgroup distance functions［J］.Lecture Notes in Computer Science，2007，37(4450):61－75.

NEW Public Key Cryptosystem Using Non-Abelian Algebra Structures

LI Shao-hua，SHANG Xu-feng

(Colleg of Science，China Jiliang University，Hangzhou 310018，China)

Propose a new Diffie-Hellman key exchange scheme based on non-Abelian algebra structures and also propose a new public key cryptosystem based on the proposed scheme.The security of this scheme relies on the difficulty of a base problem，which combines the conjugacy search problem with the Diffie-Hellman problem，and which is a transformation problem.At last，apply the proposed cryptosystem to a signature scheme which is similar to ElGamal scheme.

non-Abelian algebra structure;Diffie-Hellman key exchange scheme;twisted conjugacy search problem;public key cryptosystem

TP309.7

A

1007－0834(2011)03－0035－02

10.3969/j.issn.1007－0834.2011.03.012

2011－05－23

国家自然科学基金资助项目(11071081);浙江省自然科学基金杰出青年团队项目(R1090138)

李绍华(1986—)，男，黑龙江哈尔滨人，中国计量学院理学院.