三类恰当有效解集在正锥下的等价性和存在性

粟其峰

(贵州大学理学院,贵州 贵阳 550025)

三类恰当有效解集在正锥下的等价性和存在性

粟其峰

(贵州大学理学院,贵州 贵阳 550025)

证明了 Ge恰当有效解、Be恰当有效解和 He恰当有效解在正锥下的等价性,且在此基础上,由在非空紧凸集上似凸多目标最优化问题的 Ge恰当有效解的存在性,得出Be恰当有效解、He恰当有效解的存在性.

多目标最优化;Ge恰当有效解;Be恰当有效解;He恰当有效解;等价性;存在性

在多目标最优化问题的研究中,围绕最优解,涌现了很多成果,也产生了不少于 20种有影响的解的概念,如绝对最优解,有效解,弱有效解,Ge恰当有效解等[1-4].

但由偏序定义的多目标最优化问题的 Pareto有效解和锥有效解,都仅是问题在某种意义下的非劣解,一般来讲,在这种意义下的解的集合都会相当大,而恰当有效解正是从有效解类中定义出的具有更好性能的解,恰当有效解的定义最先是由 KUHN和 TUCKER引入的[6],恰当有效解的概念较多,本文只介绍和研究三类恰当有效解,如 1968年 GEFFR ION A M[7]提出有明显经济背景的 Ge恰当有效解,1979年BENSON H P[8]提出的 Be恰当有效解和 1982年 HEN IGM I[9]提出的 He恰当有效解.解的存在性是多目标最优化研究中的一个重要课题,恰当有效解的存在性研究也出现一些结果[5],然而恰当有效解的概念较多,研究不同解之间在一定条件下的关系和同时存在性对今后的学习就很有意义.

本文首先证明了 Ge恰当有效解、B e恰当有效解和 He恰当有效解在正锥下的等价性,然后由非空紧凸集上向量目标函数是似凸的多目标最优化问题的 Ge恰当有效解的存在性,得出 B e恰当有效解、He恰当有效解的存在性.

1 预备知识

考虑多目标优化问题

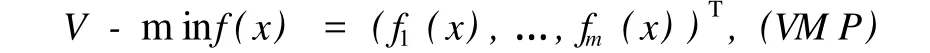
其中,X⊆ Rn是非空集合,f:Rn→Rm是向量函数.

记问题 (VM P)的 Pareto有效解集为 E(f,X).

2 等价性和存在性

因此,由定理 3可得 Ge(f,X)=B e(f,X)Rm+=He(f,X)Rm+=φ.也即在正锥的条件下,紧凸集上向量目标函数是似凸的多目标最优化问题的 Be恰当有效解、He恰当有效解和 Ge恰当有效解是等价的且是同时存在的.

[1]SANARAGI Y,NAKAYYAMA H,TAN INO T.Theory ofMulti-objective Opt imazation[M].New York:Academic Press,1985:412-455.

[2]林锉云,董加礼.多目标优化的方法与理论[M].吉林:教育出版社,1992:21-55.

[3]胡毓达.多目标规划有效性理论[M].上海:科学出版社,1994:186-216.

[4]徐玖平,李军.多目标决策的理论与方法[M].北京:清华大学出版社,2006.

[5]胡毓达,杨雷,李静.多目标最优化 G-恰当有效解集的存在性和连通性[J].运筹学报,2004,8(2):72-80.

[6]KUHN H W,TUCKER A W.Nonliner Programming:Proceedongs of the Second Berklet Symposium onMathematicial Statistics and Probaility,Berkeley,July 31-August 12,1950[C].Berkeley:University of California Press,1951.

[7]GEOFFR ION A M.Proper efficiency and the theory of vectormaximization[J].Journal ofMathematicalAnalysis&Applications,1968,22:618-630.

[8]BENSON H P.An improved definition of proper efficiency for vectorminimization with respect to cones[J].J.Math.Anal.Appl.,1979,71:232-241.

[9]HEN IGM I.Proper efficiencywith respect to cones[J].J.Optim.TheoryAppl.,1982,36:387-407.

Equivalence and Existence of Three Types of Appropriate Efficient Solution Set under the Positive Cone

SU Qi-feng

(College of Science,Guizhou University,Guiyang 550025,China)

In the report,properly efficient solutionsofGe,B eandHewere proved in the cone under the equivalence.Based on it,withGeexistence of properly efficient solutions of the non-empty compact convex set to be convexmulti-objective opt imization problem,Beproperly efficient solution andHeproperly efficient solution of the problem were obtained.

multi-objective optimization;Geproperly efficient solution;Beproperly efficient solution;Heproperly efficient solution;equivalence;existence

O 221.6 < class="emphasis_bold">文献标志码:A

A

1004-1729(2011)02-0117-03

2011-03-21

国家自然科学基金 (10771042)

粟其峰 (1983-),男,湖南邵阳人,贵州大学理学院 2009级硕士研究生.