利用偏微分方程的 Tetrolet变换图像去噪

李财莲,孙即祥,康耀红,李智勇

(1.国防科学技术大学电子科学与工程学院,湖南长沙 410073;2.海南大学信息科学技术学院,海南海口 570228)

利用偏微分方程的 Tetrolet变换图像去噪

李财莲1,2,孙即祥1,康耀红2,李智勇1

(1.国防科学技术大学电子科学与工程学院,湖南长沙 410073;2.海南大学信息科学技术学院,海南海口 570228)

对图像进行 Tetrolet变换后利用偏微分方程对图像进行了质量改善,仿真结果表明,该算法不仅能有效去除噪声,而且可得到更高的峰值信噪比和更好的视觉效果,去噪后图像较光滑,减少了方块效应,更多地保留了图像边缘和细节等局部特征.

Tetrolet变换;方块效应;偏微分方程;图像去噪

近 20年来,由于多尺度几何分析能有效地表示二维图像中具有多方向性的边缘和纹理等几何特性,被广泛应用到图像处理的各个领域,并在图像去噪中取得了很大的成功.基于偏微分方程 (PDE)的图像处理方法在平滑噪声的同时可以使边缘得到保持,因此,在图像处理与分析领域里也得到了广泛的重视,成为图像处理与分析中的一个重要工具[1-2].

由于多尺度几何分析与偏微分方程各有特点,很多学者结合了多尺度几何分析方法与偏微分方程对图像进行处理[3-7],取得了很好的处理结果.如文献[3]分别结合 Ridgelet,Curvelet与变分能量最小 TV(TotalVariation)方法对图像进行重构,很好地保持了图像的边缘特征;文献[4]结合Wavelet变换与各向异性扩散方程对图像进行边缘保持,同样取得了很好的视觉效果;文献[5]结合复数 Ridgelet变换与变分能量最小 TV方法对图像进行去噪,去噪后的图像在保留图像细节方面比较理想;文献 [6]结合 Curvelet变换与非线性扩散方程来对图像进行去噪处理,也取得比较优异的效果.同样,文献[7]结合 Shearlet变换与变分能量最小 TV方法对图像进行去噪也取得优异的效果.

2009年,KROMMWEH J提出了一种新的自适应 Haar小波变换—Tetrolet变换[8-10],理论简单,但有效,能很好地表示图像的几何结构特性,能对图像进行更稀疏的表述,且系数的能量非常集中,因而去噪能力强.由于 Tetrolets非常小的支撑域,使得 Tetrolet变换不受 Gibbs振荡的影响[11],其缺点是由于块区域基本功能函数的不平滑,使得去噪后图像存在方块效应,并且当噪声方差越来越大时,去噪后图像方块效应越来越严重,严重影响去噪后图像主观质量.因此,笔者利用偏微分方程来改善 Tetrolet变换后的去噪图像质量,减少方块效应,提高视觉效果.

1 基本原理

1.1 基本定义函数 u:Ω→R表示原始图像,其中Ω表示图像域,Ω⊂ R2,u是未知的;函数 I:Ω→R是已知与 u同场景的观测图像,图像处理与分析的目的是从已知的 I得到原始的 u.引入一个连续的尺度参数t[0,τ],根据尺度 t取值的不同,就可以得到不同尺度下处理的图像,原图像对应于尺度 t=0时的图像.设 n=n(x,y)为独立同分布高斯白噪声,采用的经典降质模型为

这是一个线性位移不变、加性高斯噪声的模型.图像去噪的目的是根据观测值 I找到图像的估计值 ^u使得其与清晰图像 u的均方误差最小.

1.2 Tetrolet变换[8-10]Tetrolet变换构建类似于 Wedgelet变换,在边缘部分应用了 Haar功能函数.先将图像分成 4×4块,然后在每一块中确定与图像几何结构相适应的四格拼板.由于四格拼板 Tetrominoes是最先被应用到一种拼板游戏中用的多边形拼合板,因此 KROMMWEH J将这种多尺度多方向变换称之为 Tetrolet变换,图 1为 Tetrolet变换的结构示意图.由于四格拼板与块图像中的几何特性自适应,因此 Tetrolet变换能更好地保持图像边缘和方向纹理等信息,在图像压缩、去噪和非线性近似中非常有效,其基本原理详见文献[8-10].

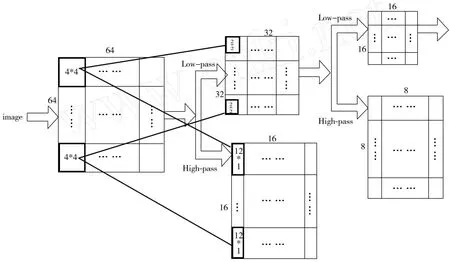
图1 Tetrolet变换结构

1.3 偏微分方程目前偏微分方程在图像处理中的应用主要可以分为 3类[12]:第 1类是基于尺度空间公理体系的偏微分方程模型,主要是从方向滤波器的角度分析和设计方向扩散方程,代表算法为 PERONA和MAL IK提出的各向异性扩散模型 (P-M模型);第 2类是基于泛函变分角度而导出的偏微分方程,基本思想是确定图像的能量函数,通过对能量函数的最小化过程,使得图像达到平滑状态,代表算法广泛应用的总变分 TV模型和四阶模型;第 3类为 RUD IN和 OSHER提出了一种冲激滤波模型,是一种双曲型的偏微分方程模型,可用于图像的增强和去模糊.

(1)P-M模型[13]

PERONA P与MAL IK J提出将一种非线性扩散方程 (P-M方程)应用到尺度分析中,在逐渐减少细节的同时,边缘保持清晰,其滤波原理是在图像不同特征处进行不同程度的平滑,即在区域内部,平滑程度提高,在靠近边缘处,减少平滑,从而既滤除细节及噪声,又保持边缘.其偏微分方程为

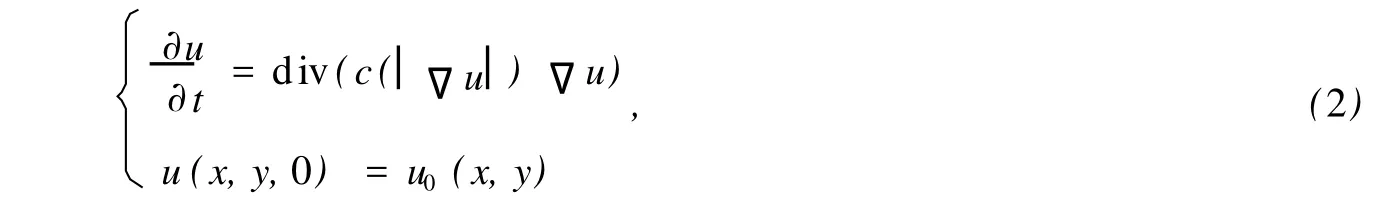
再对 u0-^u部分进行偏微分方程处理,利用有限差分法来求解.其具体算法步骤如下:

步骤1 u0=u0,j=0;

步骤 2 对 uj进行 J层 Tetrolet变换,得到 Tetrolet系数与近似系数,对 Tetrolet系数进行硬阈值操作,进行逆 Tetrolet变换后得到 uc,即:uc=T-1(S(T(uj))).T表示 Tetrolet变换,T-1表示逆 Tetrolet变换,S表示硬阈值操作;

步骤 3 对 v=u0-uc进行 P-M处理或 TV处理,利用有限差分法得到 vj;

步骤4 uj=uc+vj;

步骤 5 判别:如果 j满足迭代终止条件,则转步骤 7;否则转步骤 6;

步骤 6 j=j+1,重复步骤 2～5;

步骤 7 输出去噪后图像 ^u=uj.

3 仿真实验

为了验证本文提出的去噪算法的有效性,选择标准测试图像 Lena,Boat与 Polygons并将彩色图像灰度化,叠加均值为零的高斯白噪声进行实验.用Matlab7.0对新去噪算法进行了验证,并与经典的 Tetrolet变换去噪算法进行了对比.

为表述方便,用“TT”表示经典的 Tetrolet变换,“TT+PM”表示经典 Tetrolet变换与 P-M方程相结合算法,“TT+TV”表示经典 Tetrolet变换与 TV模型相结合算法,去噪阈值选取经典的 t=3σ.

图2～4给出了部分图像去噪时的结果,为了比较方便,只给出了局部图像.

图2 ‘Lena’部分图像去噪σ=40

图3 ‘Polygons’部分图像去噪σ=50

图4 ‘Boat’部分图像去噪σ=10

为更好地对本算法进行对比实验,将经典的Wavelet,Contourlet变换应用于图像去噪中,同样利用偏微分方程来对图像质量进行改善,为表述方便,用“WT+PM”表示经典Wavelet变换与 P-M方程相结合算法,“WT+TV”表示经典 Wavelet变换与 TV模型相结合算法,“CT+PM”表示经典 Contourlet变换与P-M方程相结合算法,“CT+TV”表示经典 Contourlet变换与 TV模型相结合算法,去噪阈值同样选取经典的 t=3σ.表 1～3列出了几种算法去噪后图像 PSNR值比较结果.

从表 1～3和图 2～4中可以看出:

1)本算法在有效去除噪声的同时,减少和改善了方块效应,提高了视觉效果,去噪后图像相对经典算法较光滑,并更多地保留了图像细节和纹理,如图 2～4所示.

2)当噪声方差较少 (如σ=10)时,使用硬阈值函数去噪,虽然经典的 Tetrolet变换能得到比本算法稍高的 PSNR值,但从视觉效果来看,其方块效应比较明显,不如本算法光滑,如图 4所示;当噪声方差越来越大时,经典算法去噪后图像方块效应越来越严重,严重影响去噪后图像视觉效果,而本算法当噪声方差越来越大时,可以取得更好的去噪效果,更高的 PSNR值,更好的视觉效果,如图 2～3所示.

3)在实验中,Tetrolet变换和 TV相结合比 Tetrolet变换与 P-M相结合保持更多的边缘和纹理特征,相对边界要清晰一些,方块效应得到明显的改善,其主要原因是 P-M方程是一个各向同性的扩散方程,即对图像中的每一点,其扩散强度相同,特别地,图像在同质区域和沿着边缘同样被平滑了,这就造成结果图像在去噪的同时,模糊了边缘,而 TV模型的主要优点是能保持边缘.

4)相比于经典的Wavelet,Contourlet变换与偏微分方程相结合算法,本算法由于 Tetrolet变换能对图像进行更稀疏的表示,因而去噪后图像有更高的 PSNR值,其 PSNR值提高 0.5～0.2 dB(如表 1～3所示).

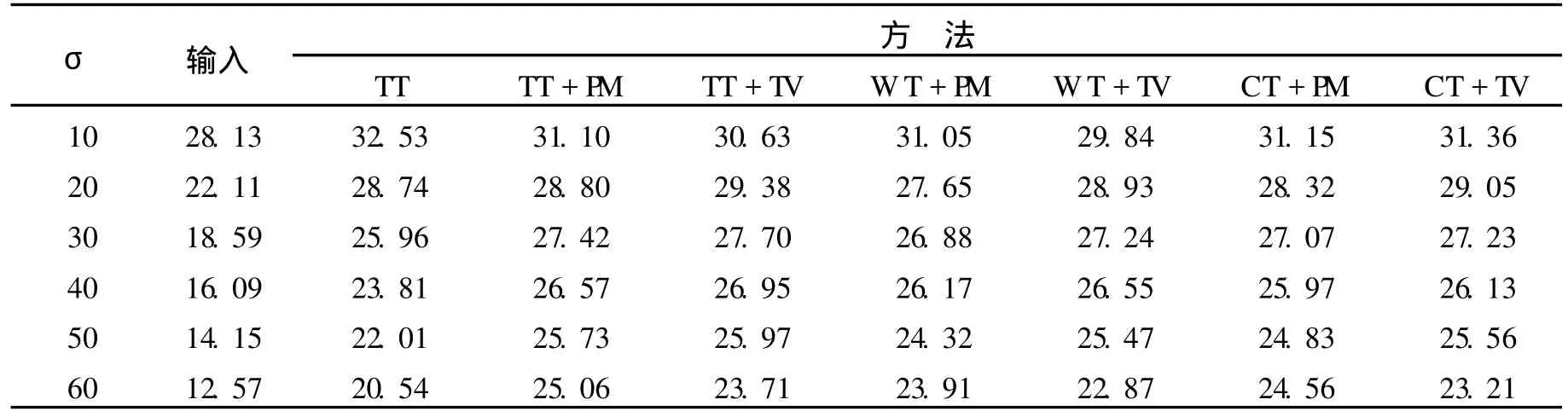
表1 各种方法对 Lena 512×512去噪后 PSNR值比较 dB

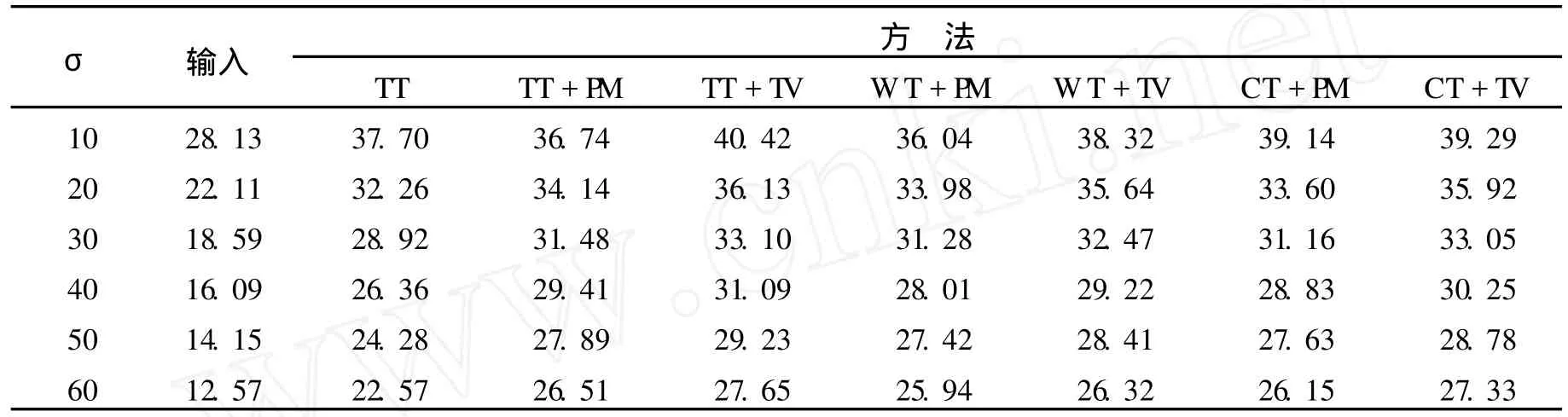
表2 各种方法对 Polygons 512×512去噪后 PSNR值比较 dB

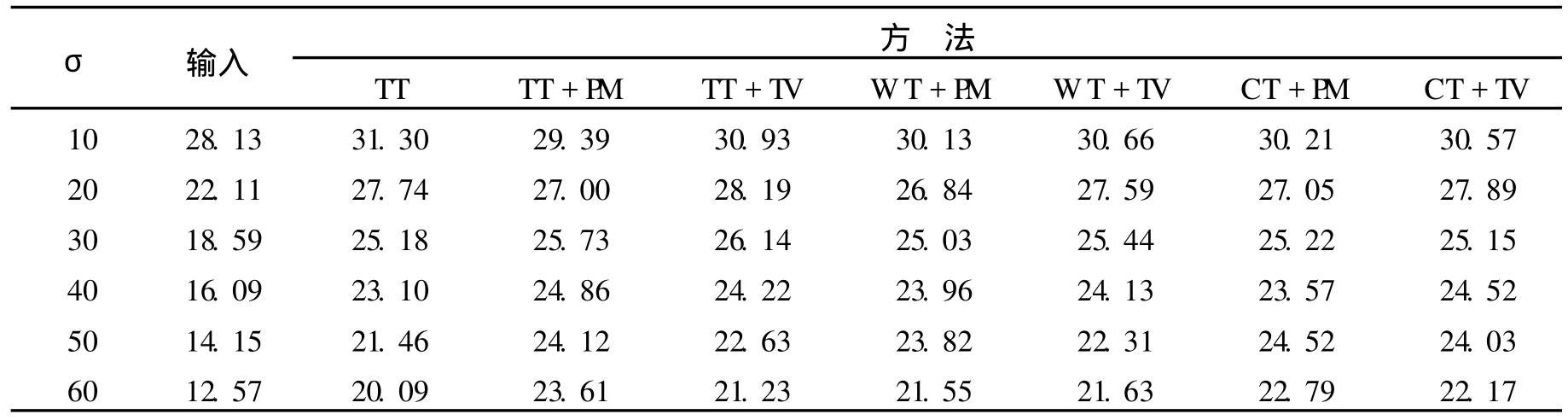
表3 各种方法对 Boat 512×512去噪后 PSNR值比较 dB

4 小 结

本文将经典的 Tetrolet算法和偏微分方程相结合对图像进行了去噪,使得经典 Tetrolet去噪算法中的方块效应得到了一定的改善和抑制,混合算法去噪后图像相对经典变换算法去噪后图像较平滑,且更多地保持了原始图像的边缘和细节等局部特征,进一步提高了去噪图像的主客观质量,实验结果表明本文算法是有效可行的.

[1]杨新.图像偏微分方程的原理与应用[M].上海:上海交通大学出版社,2003.

[2]张红英,彭启琮.数字图像修复技术综述[J].中国图像图形学报,2007,12(1):1-10.

[3]CANDES E J,GUO F.New multiscale transforms,minimum total variation synthesis:Applications to edge-preserving image reconstruction[J].Signal Process,2002,82:1519-1543.

[4]FONTA INE F,BASU S.Wavelet-based solution to anisotropic diffusion equation for edge detection[J].Int.J. Imaging Sys.Tech,1998,9:356–368.

[5]MA J W,FENN M.Combined complex ridgelet shrinkage and total variation minimization[J].S IAM J.Sci.Comput.,2006,28(3):984–1000.

[6]MA J W,PLONKA G.Combined curvelet shrinkage and nonlinear anisotropic diffusion[J].IEEE Trans. Image Proc.,2007,16:2198-2206.

[7]EASLEY G R,LABATED,COLONNA F.Shearlet based total variation for denoising[J].IEEE Trans. Image Proc.,2009,18(2):260-268.

[8]KROMMWEH J.Tetrolet Transfor m:A New Adaptive HarrWaveletAlgorithm for Sparse Image Representation[J].Vis.Commun. Image R.,2010,21(4):364-374.

[9]KROMMWEH J,PLONK G.Directional HaarWavelet Frames on Triangles[J].Appl.Comput.Har mon.Anal.,2009,27(2):215-234.

[10]KROMMWEH J.An Orthonor malBasis ofDirectional HaarWavelets on Triangles[J].Results inMathematics,2009,53(3/4):323-331.

[11]KROMMWEH J,MA Jian-wei.Tetrolet ShrinkagewithAnisotropic TotalVariationMinimization for ImageApproximation[J].Signal Process.,2010,90(8):2529-2539.

[12]徐雷.基于偏微分方程的图像恢复研究[D].江苏:南京理工大学,2007.

[13]PERONA P,MAL IK J.Scale space and edge detection using anisotropic diffusion:processeding of IEEE Comp.Soc.Workshop on ComputerVision,MiamiBeach,Nov.30-Dec.2,1987[C].Washington:IEEE Computer Society Press,1987:16-22.

[14]RUD IN L I,OSHER S,FATE M I E.Nonlinear total variation based noise removal algorithms[J].Physica D,1992,60:259-268.

Tetrolet Shr inkage with Part ialD ifferent ial Equations for I mage Denoising

L ICai-lian1,SUN Ji-xiang1,KANG Yao-hong2,L I Zhi-yong1

(1.College of Electrical Science and Engineering,NationalUniversity ofDefense Technology,Changsha 410073,China;2.College of Infor mation Science and Technology,Hainan University,Haikou 570228,China)

After tetrolet transform was applied to the noise images,the conventional s mooth shrinkage results were further processed by partial differential equations.The simulation results indicated that the method not only remove the noise effectively,but also can obtain higher PSNR(Peak Signal to Noise Ratio)and better visual effects.Compared with typical tetrolet transform,the denoised images by our method were smoother,and the blocking artifactswere reduced,and which preservedmore significant infor mation oforiginal images,such as edges and details.

Tetrolet transfor m;blocking artifacts;partial differential equations;image denoising

TP 391 < class="emphasis_bold">文献标志码:A

A

1004-1729(2011)02-0166-06

2010-12-05

国家自然科学基金项目 (40901216);国防预研资助项目 (513220206)

李财莲 (1973-),女,湖南涟源人,海南大学信息科学技术学院工程师,国防科学技术大学电子科学与工程学院 2007级博士研究生.