受土体侧移作用既有轴向受荷单桩的简化算法
梁发云,于 峰,黄茂松
(1.同济大学 地下建筑与工程系,上海200092;2.同济大学 岩土及地下工程教育部重点实验室,上海200092)
基坑或隧道开挖等引起的土体侧移将会对邻近桩基产生作用,在此情况下,邻近桩基上既有轴向荷载与这种土体侧移形成耦合作用,使桩上产生附加的变形和内力,从而对既有轴向受荷桩的安全构成潜在威胁.既有轴向受荷桩在附加土体侧移作用下所引起的工程事故问题时有发生,姚国圣等[1]对此类问题进行了简要评述.
目前岩土工程界对于土体侧移与轴向荷载耦合作用的分析还较少.在实际工程中,按轴向受荷桩进行设计的桩基,由于种种原因,在使用期间受到了土体侧移作用,附加的土体侧移在设计阶段一般没有加以考虑,轴向荷载会与土体侧移产生耦合作用,即P-Δ效应,可能导致桩基产生较大的侧向附加荷载和弯曲变形,甚至发生折断破坏.因此,土体侧移对既有轴向受荷桩承载性状的影响不容忽视.如何对土体侧移作用下既有轴向受荷桩的承载性状进行分析,已成为岩土工程近期亟待研究的一个重要问题.国外学者如Chen等[2],Guo和Ghee[3]采用室内模型试验对此类问题进行了一些探索.在理论研究方面,对于土体位移作用下被动桩问题常用分析方法主要有整体分析法和两阶段法[4],其中由Poulos等[5]提出的两阶段法较为简便.Yokoyama Yukimitsu[6]曾指出:同时承受轴力和水平力作用的桩,严格地来说,应力的叠加原理是不适用的,需要采用耦合方法进行分析.文献[7]在研究轴向和横向荷载作用的桩基时考虑了两者的相互影响,对于研究土体侧移与轴向荷载耦合作用具有参考价值.
需要注意的是,Poulos[8]通过数值分析指出,土体位移作用不能简单地等效为荷载的作用.由于土体位移作用的复杂性,对于轴向荷载与水平位移耦合作用的被动桩分析,目前鲜有文献报道.
本文基于Winkler地基模型和两阶段法,结合弹性桩的挠曲微分方程,提出了一种土体侧移与轴向荷载耦合作用下单桩性状的简化算法,与已有文献的对比验证了本文方法的可行性,并通过参数分析研究土体侧移对既有轴向受荷单桩性状的影响.
1 土体侧移下既有轴向受荷单桩简化算法
1.1 基于Winkler地基模型的两阶段法
两阶段法是Poulos等[5]针对受土体位移作用的被动桩问题而提出的.本文在该方法的基础上进一步引入了桩身轴力的作用,将该方法推广至受土体侧移作用的轴向受荷单桩性状分析.
两阶段法将被动桩的分析分为两个阶段,第一阶段得到没有桩时的自由土体位移,第二阶段将自由土体位移作为已知条件,施加于单桩,计算单桩的反应.桩土相互作用的计算模型采用如下假定:①基于Winkler地基模型将桩视作弹性地基梁;②土体为连续变形体;③桩与土之间的相互作用采用弹簧模拟,桩土紧密接触且变形协调.
假设土体位移引起的自由土体位移为hs(z),在桩基的作用下,土体的自由位移受到约束,设桩身的最终侧向位移为U(z),基于桩土变形协调假定,该位移即为土体的最终侧向位移.土体的约束位移也就是 桩土的相对位移为Δ=hs(z)-U(z),由Winkler地基模型,约束位移产生的桩侧土压力为

式中,kz为桩周土的基床反力模量,kN·m-2,可定义为桩身某处单位长度上桩周土的抗力与桩土相对位移的比值.
本文采用Vesic[9]所提出的基床反力模量kz确定方法,该方法将基床反力模量与土体的弹性参数和土的泊松比联系起来的,表示如下:

式中:Es为土体的弹性模量,kPa;ν为土的泊松比;EI为桩的抗弯刚度,kN·m2;d为桩的直径,m.
1.2 土体侧移下既有轴向受荷单桩的挠曲微分方程
将桩视作弹性地基梁,建立土体侧移作用下既有轴向受荷单桩的挠曲微分方程如式(3),方程中的第2项是为了考虑轴力影响而引入的轴力影响项.

式中,Nz为桩在z深度处承受的轴力,kN.
结合式(1),可以得到土体水平位移对单桩影响的水平位移控制微分方程:

受到微分方程求解的限制,只有均质土体的情况(即kz沿深度不变)可直接求解得到解析解.而天然土体大多为分层地基,此时可采用有限差分法进行求解.将桩离散为n个长度为δ的单元后,式(4)可转化为对第i节点(i=0,1,2,…,n)的差分方程.
求解差分方程时由于桩顶和桩底处存在U-2,U-1以及Un+1,Un+2等虚拟节点的桩身侧向位移,故需要利用式(5)的位移与弯矩、转角之间的关系,并结合式(6)的桩顶和桩底边界条件来消除这些待定项之后方可进行求解.

(1)对于顶端自由的桩,桩顶施加有剪力H,弯矩M,得到两个边界条件:

式中,Ui表示i节点处的桩身侧向位移,其中U-2,U-1表示桩顶处两个虚拟节点的位移.
(2)若顶端固定,桩顶无位移和转角,则得:
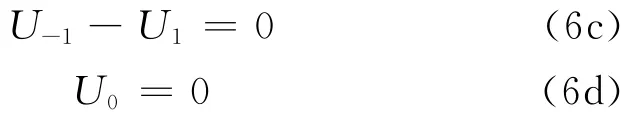
(3)若顶端约束位移不约束转动,则得:
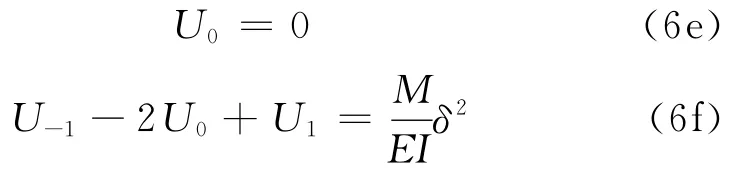
同理,桩底节点根据其边界条件也可得到上述类似方程.消去待定项后求解矩阵方程,可求得桩身各个节点的位移.将节点位移回代到式(6),即可求得各节点的弯矩.
2 算例验证
2.1 与离心试验结果对比(桩顶无轴力作用)
Leung等[10]通过离心模型试验研究了基坑开挖引起的土体侧移对桩的影响,桩顶无轴力作用.本算例采用文献[10]的试验参数,其中基坑开挖深度为4.5m,桩到基坑的距离为3m;桩长为12.5m,桩的直径为0.63m,EI=2.2×105kN·m2;土体弹性模量按照深度z变化规律为Es=6z(MPa);自由土体位移按文献[10]的试验实测结果取值,如图1中虚线所示;桩顶约束条件为桩顶水平位移为零,但不约束转角.
利用本文方法计算所得的水平位移和弯矩与实测数据对比如图1和图2所示,本文计算结果与实测数据基本吻合,验证了本文方法在桩顶无轴力作用时的适用性.

图1 与文献[10]算例的位移对比Fig.1 Comparison of displacements with Reference[10]

图2 与文献[10]算例的弯矩对比Fig.2 Comparison of bending moments with Reference[10]
2.2 与LPile软件结果对比(桩顶有轴力作用)
目前关于桩受水平位移与轴力耦合作用的算例鲜见文献报道,为验证本文算法的合理性,与LPile软件计算结果进行了比较.该软件采用p-y曲线法(即水平荷载作用下某深度处的土反力p与该点桩的挠度y之间的关系曲线)来描述水平受荷桩桩周土体的非线性变形特性.LPILE 是由美国德州奥斯汀大学Reese教授主持开发的商业软件,已成为美国工程界应用最为广泛的水平桩分析程序之一,笔者在文献[11]中对该软件进行了详细介绍.
轴向受荷桩长径比为L/d=25,截面面积为A,土体弹性模量Es与土的粘聚力cu之比Es/cu=143,fc为桩身材料的抗压强度设计值,为便于分析,可取为桩身材料弹性模量的1/1 000;桩头自由;ν=0.49.参照Poulos[12]的分析算例,假定桩受到如图3所示的土体初始位移场作用.
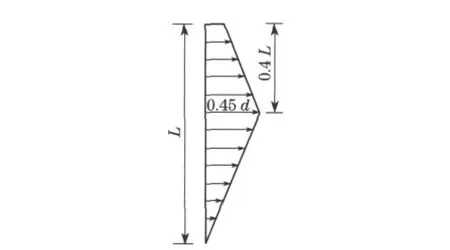
图3 土体侧移分布模式Fig.3 Displacement mode of lateral soil movement
通过量纲分析,可将桩顶承受的轴向荷载、桩身位移和弯矩等参数分别表示为桩顶压应力的量纲一值,在本算例中取KN为30%;桩身位移的量纲一值;桩身弯矩的量纲一值
将本文方法计算得到的单桩位移和弯矩与LPile软件计算结果进行对比,如图4 和图5 所示.本文算法与LPile软件计算结果基本吻合,验证了本文算法在考虑轴向荷载与土体侧移耦合作用时的可行性.本文方法与LPile软件的计算结果稍有差异,其原因主要是两种方法对于基床反力模量确定方法的不同而造成的.
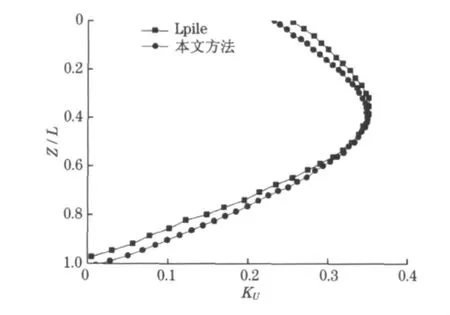
图4 与LPile软件的位移对比Fig.4 Comparison of displacements with LPile software

图5 与LPile软件的弯矩对比Fig.5 Comparison of bending moments with LPile software
3 参数影响分析
土体侧移作用将使桩身产生较大的弯矩和挠曲变形,轴向荷载也将由于桩身挠曲变形的出现而产生附加弯矩(即所谓的 “P-Δ”效应),而该附加弯矩又将影响到桩身挠曲变形的增加.土体侧移一定的情况下,P-Δ效应的影响因素主要有三个方面:①桩身的材料性质;②土体弹性模量;③桩顶的边界条件.本节针对这些参数的影响进行分析.
3.1 桩身材料对单桩及其P-Δ 效应的影响
不同材料的桩由于弹性模量以及设计强度的不同,在轴向荷载和侧向土体位移作用下表现的性质也有所不同.本节中基坑开挖深度为4.5m,桩到基坑距离为3m;桩长为30 m,桩外径0.63 m,内径0.43m;土体弹性模量Es=6z(MPa);桩顶自由;土体位移与第2.1 节中Leung 等[10]的试验结果一致.
图6,图7分别给出了C30和C80 混凝土的桩在无轴向荷载作用以及轴向荷载达到各自80%桩身强度时的位移和弯矩,图中fC30和fC80分别为C30和C80混凝土的抗压设计值,其他类同.

图6 不同桩身强度的位移对比Fig.6 Comparison of displacements with different pile’s strength

图7 不同桩身强度的弯矩对比Fig.7 Comparison of bending moments with different pile’s strength
对于沿桩长的水平位移,如图6所示,基坑开挖深度4.5m,水平位移的影响范围主要限于地表以下15m 之内,而桩长15~30m 位移很小甚至为零.
为分析混凝土强度对于桩身位移的影响,将桩顶附近位移放大后进行分析,可以发现:无轴向荷载作用时,C80混凝土桩的桩顶位移小于C30 混凝土桩,这是由于C80混凝土刚度较大,能够对土体的自由侧移产生的较大约束作用,或者说抵抗土体侧移的能力较强.但是当桩顶加载KN=80%,即同样在80%桩身强度的轴向力作用下,C80 桩顶位移则超过了C30桩,说明C80桩在同等计算条件和桩顶压应力水平下,其P-Δ效应比C30桩更为明显.
对于沿桩长的弯矩,如图7所示,弯矩的影响范围也集中于桩上方20m 以内,20~30 m 内则弯矩很小甚至为零.当桩顶无轴向荷载时,C80桩最大弯矩大于C30弯矩,并且最大弯矩深度较C30桩略深一些,但都在7.5~8.0m 左右.当桩顶加载80%桩身强度的轴向力时,两种材料的桩身最大弯矩的深度都有向上变化的趋势,最大弯矩值都增大,但是C80增大的幅度要比C30更大.
为了进一步研究桩身材料对P-Δ效应大小影响的规律,本文试算了6种桩身材料在相同计算条件下桩身位移和弯矩相对于无轴向力时的增幅情况,如图8和图9 所示,图中fc是与横坐标相对应的混凝土抗压设计值,fC50为C50混凝土的抗压设计值,可得出了如下一些结论.

图8 桩顶位移增幅对比图Fig.8 Comparison of increase in displacements of pile head

图9 最大弯矩增幅和最大弯矩深度对比Fig.9 Comparison of increase in maximum moments and corresponding depths
(1)当桩顶作用有相对于材料强度同等比例的轴力时,随着材料标号越大,P-Δ效应也越大.由图可见,在80%桩身强度的荷载作用下,C20桩较无桩顶轴力时位移仅增大了3.3%,弯矩仅增大了1.6%,C80相应增加了9.5%和8.2%.
(2)当桩顶轴力绝对值相同时,随着材料标号的增大,P-Δ效应减小.这一点从图8、图9中的曲线4可以看出,各种材料桩都作用有0.8fc50A的轴力,C20位移和弯矩分别增大了7.3%和5.8%.这是因为在相同的轴力下,桩的EI值越大,抵抗P-Δ效应的能力就越强.
(3)P-Δ效应作用结果不符合叠加原理.如图8和图9 所示,两图中曲线1 分别代表轴向荷载为0.4fcA时桩顶位移和最大弯矩的增幅,曲线2分别代表轴向荷载为0.4fcA时桩顶位移和最大弯矩的增幅的2倍,曲线3 分别代表轴向荷载为0.8fcA时桩顶位移和最大弯矩的增幅.可见轴向荷载为0.8fcA时的增幅大于0.4fcA时增幅的2倍.这表明了P-Δ效应对荷载和位移的影响不符合简单的叠加效应.
3.2 土体弹性模量对单桩及P-Δ 效应的影响
桩土相互作用中,土体的性质非常重要,特别在Winkler地基模型中,土体弹性模量决定了土体对桩基作用力的大小.本节旨在研究相同土体侧移模式下土体弹性模量的影响,采用与第3.1节相同的计算模型.图10和图11中绘制了C50混凝土的桩在Es=2z(MPa)和Es=6z(MPa)两种弹性模量分布下的位移和弯矩,z为地面以下深度,土体弹性模量沿深度线性变化.

图10 不同土体弹性模量的位移对比图Fig.10 Comparison of displacements with different elastic modulus of subsoils
如图10和图11所示,在桩顶有轴向力时两种土体弹性模量分布模式下的位移和弯矩都出现了增大的趋势.同时,土体弹性模量分布模式Es=6z在无轴向荷载以及有轴向荷载时位移和弯矩分别大于Es=2z相应条件下的位移和弯矩.这是因为在土体弹性模量大的时候对桩的抵抗作用也就越大.

图11 不同土体弹性模量的弯矩对比图Fig.11 Comparison of bending moments with differentelastic modulus of subsoils
Leung等[10]认为:对于密砂,弹性模量分布宜取Es=6z至Es=8z之间.图12中选取了Es=8z,6z,4z,2z,z五种分布模式,计算了对C50混凝土桩的影响情况,得到了以下结论:
(1)随着土体弹性模量的减小,P-Δ效应增大.这是因为当土体弹性模量减小时土体对桩的侧向支撑减小,引起了更大的附加弯矩和位移.
(2)土体弹性模量较大时,桩顶位移增幅大于最大弯矩增量,但随着弹性模量的减小,最大弯矩的增幅将逐渐超过桩顶位移的增量.料强度

图12 不同土体弹性模量的桩顶位移、最大弯矩增幅对比图Fig.12 Comparison of increase in displacements of pile head and max moments with different elastic modulus of subsoils
通时过,以高上强?的度参桩数身?分材析料可的知P,-当Δ充 效分?应利比用低桩强身材度桩身材料的要大,而土体弹性模量低时P-Δ效应比土体弹性模量高时的要大.因此,当模型试验采用钢管、铝管来模拟桩基受土体侧移和轴向荷载耦合作用时,而所用的模型土又偏软弱时,可能会导致试验测得的耦合效应比实际工程的偏大,这一点在实际应用时应引起必要的注意.
3.3 桩顶约束条件对单桩及其P-Δ 效应的影响
不同桩顶约束条件对桩身变形和桩土相对位移产生明显影响,从而影响桩最终的受力状态;不同约束条件下桩的P-Δ效应也显著不同.
无初始轴向荷载的C50 混凝土桩在弹性模量Es=2z土中受到同第3.1节的土体侧移作用,其余参数也与第3.1节相同,则在不同桩顶约束条件下算得的位移和弯矩如图13和图14所示.

图13 不同桩顶约束条件的位移对比图Fig.13 Comparison of displacements with different boundary conditions of pile head

图14 不同桩顶约束条件的弯矩对比图Fig.14 Comparison of bending moments with different boundary conditions of pile head
由图13和图14可见,当桩顶自由时,由于桩顶缺乏有效约束,桩顶位移将相对较大,造成既有结构有过大变形和使用性能下降,但是由于桩顶约束放松,桩身的弯矩较小,对于桩身受力是有利的.当桩顶约束位移而不约束转动时,最大位移出现在约5 m 深度处,桩的变形明显减小,但弯矩相对桩顶自由时的作用方向相反且绝对值有所增大;当桩顶完全固定时,桩的变形进一步减小,但桩顶出现了较大的正弯矩.因此,在桩身材料相同的情况下,桩顶固定时的受力最为不利.
其次,在P-Δ效应上,如图15所示桩顶自由时由于桩顶有较大的侧向变形,且缺乏有效支撑.故当承受KN=80%的轴向荷载时,桩的最大水平位移和最大弯矩相对于无轴向荷载时增大了12.2%和11.0%.而当桩顶存在有效约束时,这个增幅则将大幅减小.即桩顶约束的存在明显降低了土体侧移和既有轴力耦合作用带来的附加不利影响.

图15 不同桩顶约束条件的最大位移、最大弯矩增幅对比Fig.15 Comparison of increase in maximum displacements and maximum bending moments with different boundary conditions of pile head
4 结语
本文基于Winkler地基模型,引入桩身轴力作用建立了近似考虑土体侧移与轴向荷载耦合作用下的单桩挠曲微分方程,并采用两阶段法进行求解.分析结果表明,相对于土体侧移单独作用时,土体侧移与轴向荷载耦合作用所产生的P-Δ效应对于桩基受力和变形特性具有一定的影响.
通过对桩身材料、土体弹性模量以及桩顶约束条件等影响因素的分析,研究了这些因素对受土体侧移作用轴向受荷单桩承载性状的影响程度,其中桩顶约束条件对桩的位移和弯矩分布特性具有显著影响.同时算例分析也表明了由于P-Δ效应,土体侧移与轴向荷载的耦合作用确实不符合简单的叠加效应.结合Poulos等[12]提出的桩-桩相互作用系数概念,本文分析方法还可以进一步推广到群桩受土体侧移与轴向荷载耦合作用的分析中.
[1] 姚国圣,梁发云,李镜培,等.土体侧移作用下轴向受荷单桩承载性状三维数值分析[J].同济大学学报:自然科学版,2011,39(1):1.YAO Guosheng,LIANG Fayun,LI Jingpei,et al.3Dnumerical analysis for behavior of axially loaded pile subjected to lateral soil movement[J].Journal of Tongji University:Natural Science,2011,39(1):1.
[2] Chen C C,Takahashi A,Kusakabe O.Change in vertical bearing capacity of pile due to horizontal ground movement[M]// Physical Modelling in Geotechnics.Rotterdam:Balkema Publishers,2002:459-464.
[3] Guo W D,Ghee E H.Behavior of axially loaded pile groups subjected to lateral soil movement[C]// Proceedings of Sessions of GeoShanghai.Shanghai:GSP,2006,153:174-181.
[4] 黄茂松,张陈蓉,李早.开挖条件下非均质地基中被动群桩水平反应分析[J].岩土工程学报,2008,30(7):1017.HUANG Maosong,ZHANG Chenrong,LI Zao.Lateral response of passive pile groups due to excavation-induced soil movement in stratified soils [J].Chinese Journal of Geotechnical Engineering,2008,30(7):1017.
[5] Poulos H G,Chen L T.Pile response due to excavationinduced lateral soil movement[J].Journal of Geotechnical and Geoenvironmental Engineering,ASCE,1997,123(2):94.
[6] 横山幸满.桩结构物的计算方法和计算实例[M].唐业清,吴庆荪译.北京:中国铁道出版社,1984.Yokoyama Yukimitsu.The calculation method and examples of pile foundation [M].Translated by TANG Yeqing,WU Qingsun.Beijing:China Railway Publishing House,1984.
[7] 赵明华.轴向和横向荷载同时作用下的桩基计算[J].湖南大学学报,1987,14(2):68.ZHAO Minghua.The calculation of piles under simultaneous axial and lateral loading[J].Journal of Hu’nan University,1987,14(2):68.
[8] Poulos H G.Ground movements—a hidden source of loading on deep foundations[J].DFI Journal,2007,1(1):37.
[9] Vesic A S.Bending of beams resting on isotropic elastic solids[J].Journal of Soil Mechanics and Foundation Engineering,ASCE,1961,87(2):35.
[10] Leung C F,Chow Y K,Shen R F.Behavior of pile subject to excavation-induced soil movement [J].Journal of Geotechnical and Geoenvironmental Engineering,2000,126(11):947.
[11] 梁发云,韩杰,李镜培.基坑开挖引起的土体水平位移对单桩性状影响分析[J].岩土工程学报,2008,30(Sup.1):260.LIANG Fayun,HAN Jie,LI Jingpei.A preliminary study on behavior of a single pile subject to lateral soil movement induced by excavation[J].Chinese Journal of Geotechnical Engineering,2008,30(Sup.1):260.
[12] Poulos H G,Davis E H.Pile foundation analysis and design[M].New York:John Wiley and Sons,1980.

