动态拓扑结构的多目标粒子群优化算法

任子晖,王 坚

(同济大学CIMS 中心, 上海201804)

多目标优化问题(multi-objective optimization problem ,MOP)大量地存在于科学实践、工程系统设计、社会生产活动及投资组合等问题中.近年来,越来越多的学者采用进化算法来求解多目标的优化问题,提出了各种各样的多目标的粒子群优化算法(multi-objective particle sw arm optimization ,MPSO).如Wen-Fung Leong 等[1]提出了一种基于动态群体规模和自适应局部存档的MPSO 算法,通过增加及减少粒子的规模来达到加快收敛的目的.R .Brits 等[2]提出了一种小生境的MPSO 算法,在原始种群的基础上增加一些独立优化的子群体.Praveen Kumar Tripathi 等[3]提出了一种基于时间变化权重和加速系数的MPSO 算法.含区间参数多目标系统的微粒群优化算法[4]通过概率支配关系来确定解的优劣.张利彪等[5]提出一种多子群进化算法, 并在群体中实现信息交换来保证群体分布的均匀性.曲红等[6]提出了一种动态的MPSO 算法, 对粒子位置和速度的更新公式依据杂交概率进行了动态的改进.丛琳等[7]根据多目标的特点,提出了正交免疫克隆粒子群算法.上述的MPSO 算法均缺少对其拓扑结构的分析,对于互不支配的2 个解是否进入档案库(储备集)也没有给出有效的解决办法.此外,文献[8-12] 也分别对粒子群的拓扑结构进行了改进, 但是均没有应用在多目标的粒子群优化上且在改变边的连接结构时针对性也不是很强.本文针对这些缺点给出了一种动态拓扑结构的MPSO 算法.在对粒子拓扑结构分析的基础上, 给出解的支配度和拥挤度及粒子差异性的概念, 同时对粒子的拓扑结构进行调整, 根据决策容忍系数的大小更新储备集, 由此提出了一种动态拓扑结构的MPSO 算法(dynamical topology MPSO ,DMPSO).

1 一些基本概念

通常多目标优化问题的描述如下:

式中:f(x)为目标向量, f(x)∈Rm,x ∈RD为决策变量,f i(x)是第i个目标函数;gj(x)为第j个约束条件.当∀i ∈{1 ,2,…,m}, 有f i(x*)≤f i(x)且∃i0 ∈{1,2,…,m},满足f i0(x*)＜f i0(x)时,称向量x*支配向量x .x*=(x*1,x*2,…,x*D)称为Pareto 解当且仅当不存在i0∈{1 ,2,…,m}使得f i0(x)＜f i0(x*)成立.所有Pareto 解的集合构成Pareto 最优集.所有Pareto 最优解对应的目标函数值形成的区域PF称为Pareto 最优前端或均衡面.具体参见文献[5-7] .

2 动态拓扑的多目标粒子群优化算法

PSO(particle swarm optimization)以模拟鸟的群体智能为特征,以求解连续变量优化问题为背景.在PSO 中, 每只鸟被称为一个粒子, 每个粒子用其几何位置和速度向量表示,每个粒子参考自己的既定方向及所经历的最优方向和整个鸟群所公共认识到的最优方向来确定自己的飞行.

PSO 是Kennedy 和Eberhert[13]于1995 年首先提出,为便于对粒子的拓扑结构进行分析研究, 在文献[14] 中采用式(2)对粒子群的位置xi和速度vi进行更新:

式中:v i∈[-vmax,vmax] ,vmax是常数,i=1,2,…,m;χ为影响粒子轨迹收敛的一个约束因子,通常取0 .729[15];N i为i的邻域集合;u(0,φ)是一个(0,φ)间的均匀分布的随机数, φ是加速因子, φ控制粒子的收敛速度,通常取4 .1[15];下标nbr(n)为i的第n个邻域;第i个粒子的位置用一个D维的向量xi=(x i1,x i2,…,x iD)表示, 它在空间的飞行速度其用vi=(v i1,v i2,…,viD)表示.迭代终止条件根据具体问题一般选为最大迭代次数或粒子群迄今为止搜索到的最优位置满足预定最小适应阀值.

2 .1 储备集更新策略

在多目标的求解过程中, 最关键的问题就是如何确定Pareto 最优前端, 而在最优前端确定的过程中重要的步骤就是储备集(外部档案)的更新策略.在叙述该文储备集更新策略之前先给出几个定义.

假设a,b都是非劣解, 那么a,b是互不支配的,因为a在f2方向支配b,b在f1的方向支配a.下面给出支配度的概念.

定义1 假设xi,x j为式(1)的非劣解, 若x i在f p1,f p2,…,f pk方向支配x j,x j在f q1,f q2,…,f qk方向支配x i,其中p1,p2,…,pk,q1,q2,…,qk∈{1,2 ,…,m},那么称ρ(x i,x j)为xi对x j的支配度.

其中, ρfk(xi,x j),k∈{1,2,…,m}称为x i在f k方向上对x j的支配度,其计算公式为

定义2 将目标空间按照文献[1] 的方法进行划分,每次进化后计算每一方格k内进入储备集的粒子个数N ki与整个方格内粒子数N k的比值τk(t)称为第t代时第k个方格内粒子的拥挤度.

在更新储备集时, 若储备集的大小未超过规定的定值,非劣解将直接进入储备集.若储备集的大小超过规定的定值,且新解xi支配储备集中的解x j,则新解xi将进入储备集,解xj将从储备集中删除;否则根据新解xi对储备集中解支配度的大小及新解所在方格内拥挤度的大小判断被替代的解, 这里取支配度大于给定的值且拥挤度小于给定值的解来替代储备集中的解.因为当新解xi所在方格内的拥挤度很小时, 说明此方格内进入储备集的粒子数很少,为了保证解的多样性和均匀性, 故在新解对储备集中部分解中的支配度适中情况下, 选取方格内(邻域内)拥挤度最小的解替代储备集中的部分解.

设A(t)为第t代储备集,N A(t)表示第t代储备集中元素的个数,N0 是给出的储备集中元素个数的规定值, α, β 分别为支配度和拥挤度的决策容忍系数, α, β 常取为初始的平均支配度和平均拥挤度的值,本文取值为1/3 .下面简单给出储备集更新的步骤.

若N A(t)＜N0 ,xi(t+1)进入储备集,A(t+1)=A(t)∪{xi(t+1)},N A(t+1)=N A(t)+1 ;否则判断x i(t+1)是否支配xk,xk∈A(t), 若是,A(t+1)=A(t)∪{x i(t+1)}{xk},N A(t+1)=N A(t)+1 ;否则计算ρfk(xi+1(t),x j),计算xi(t+1)所在方格k内的拥挤度因子τk(t+1),若ρfk(xi+1(t),xj)≥α,且τk(t+1)≤β ,则A(t+1)=A(t)∪{xi(t+1)}{x j},N A(t+1)=N A(t)+1,其中j∈{1 ,2,…,N A(t)};否则A(t+1)=A(t),N A(t+1)=N A(t).

2.2 动态拓扑结构的描述

粒子群的拓扑结构是指整个群体中所有粒子之间连接的方式, 而粒子群的邻域结构是单个粒子如何与其他粒子相连的方式.拓扑结构是整体性质,邻域结构是局部性质, 邻域结构决定了拓扑结构.本文的思想就是通过粒子邻域结构变化来达到改变粒子拓扑结构变化的目的.

根据2.1 节计算出储备集中每个元素所在方格的拥挤度,当拥挤度的最大值和最小值相差很大时,且以后多次迭代得到的解都分布在某一固定方格的周围,这表明拥挤度的差距还将继续增大,说明粒子的多样性不是很好,全局的搜索能力不强,需要改变粒子的邻域结构来增强全局搜索能力;反之需要改变粒子的邻域结构来增强局部搜索能力.基于这个思想,定义了粒子邻域结构数量控制的自适应函数.

其中,τk(t)为第t代时第k个方格内粒子的拥挤度。当拥挤度的最大值和最小值相差很大时,根据式(6)增加邻域粒子, 使粒子和更多的粒子交换信息, 反之减少邻域粒子, 使粒子在局部搜索更仔细.

下面介绍PSO 的两大拓扑结构Gbest 拓扑和拟小世界拓扑, 如图1Gbest 拓扑结构是指每个粒子都与系统中的其他粒子相连, 此时粒子的邻域结构比较庞大,粒子间信息的交互比较完善,导致粒子的收敛速度快,全局搜索能力较强, 但容易陷入局部最优,出现早熟现象.拟小世界拓扑结构是指每个粒子只与其周围的部分粒子相连, 粒子间的信息交流较慢,而一旦一个粒子搜索到最优位置,最终这个信息也将逐步传播到整个群体,这种拓扑结构收敛的速度较慢,但具有较强的局部搜索能力, 鲁棒性好.本文将PSO 的这2 种拓扑结构很好地结合起来, 当粒子的邻域粒子增加时,即＞N i邻域中粒子的结构采用Gbest 拓扑拓扑结构,当粒子的邻域粒子减少到＜N i时, 邻域中粒子的结构采用拟小世界拓扑结构,更加有效地平衡了粒子的全局搜索能力和局部搜索能力.下面重点介绍拟小世界拓扑结构.

图1 拓扑结构Fig.1 Topology

定义3 节点v i与节点v j之间差异度的大小定义如下:

式中,γi为节点i的度.节点差异度越小,相似度越大,说明这2 个节点间的信息差异不大,这2 个节点间无边相连,否则,节点的差异性越大,说明这2 个节点间信息的差异性越大,此时要想达到快速收敛的目的,这2 个节点间必须有边相连.

在实际操作中, 粒子间起初是全连接拓扑结构,当＜N i时, 根据节点间差异度的大小,断开一些差异度较小的边,保留差异度较大的边.为了不增加计算复杂度,在比较同一节点差异度的大小时,只需计算与给定值Z之间的关系, 当时,断开节点vi与节点v j之间的边, 否则保留此边.这里Z取为平均差异度.最后给出了一个算法收敛的定理.

定理1 算法DTMOPSO 是以概率收敛于pareto 前端的.

3 DTMOPSO 算法验证

3 .1 算法的验证

为了对上述提出的DMPSO 算法进行验证, 先针对2 个问题验证其可行性, 然后再将其应用在实际问题中, 验证算法的有效性.参数的设置如下:支配度和拥挤度α=β =1/3 ;约束因子χ=0 .729 ;加速因子φ=4 .1 ;初始粒子规模N0=100 ;最大迭代次数Nc=2 000 .下面给出2 个经典的多目标函数的测试

例子,具体形式如下:

使用上面给出的参数,得到的结果如表1 .

表1 几种算法求解问题(12)和(13)的误差结果对比Tab.1 Results comparison of DMPSO algorithmand other algorithms to problem (12)and(13)

从表1 中的结果可以看出,DMPSO 算法是有效的,但采用DMPSO 算法得到满意解需要花费的时间比较长,也就是说DMPSO 算法是在牺牲时间的基础上换回精度的.主要是因为在进行备集更新和确定动态邻域的时候花费的时间比较大.下一步将研究如何在确保精度的基础上使花费的时间也尽量减少.

3.2 算法应用于资源受限研发项目进度的问题

将DMPSO 算法用于资源受限研发项目进度的问题中,并与文献[6] 中的结果进行对比.其中编码和解码方式采用[6] 中的方式,图2 为对比结果.

从图2 可以看出DMPSO 算法应用在资源受限研发项目进度问题中得到的结果是满意的,不管是实验工期还是实验资源方差, 最后的结果都优于文献[6] 的结果.

3.3 算法应用于多目标车辆路径问题

再将DMPSO 算法应用在多目标车辆路径上的实验结果,编码和解码方式采用文献[16] 中的方式,并于文献[16] 中的结果进行了对比(表2).其中Cput是指程序运行时间;Opt定义为Pareto 解集的最优指数;Sp用来衡量Pareto 解集张成的空间的标准,其值越小,说明解的分布越均匀;Q表示问题名称,Q,Opt和Sp的具体表现形式见文献[16] ;Favar为Pareto 解的方差.

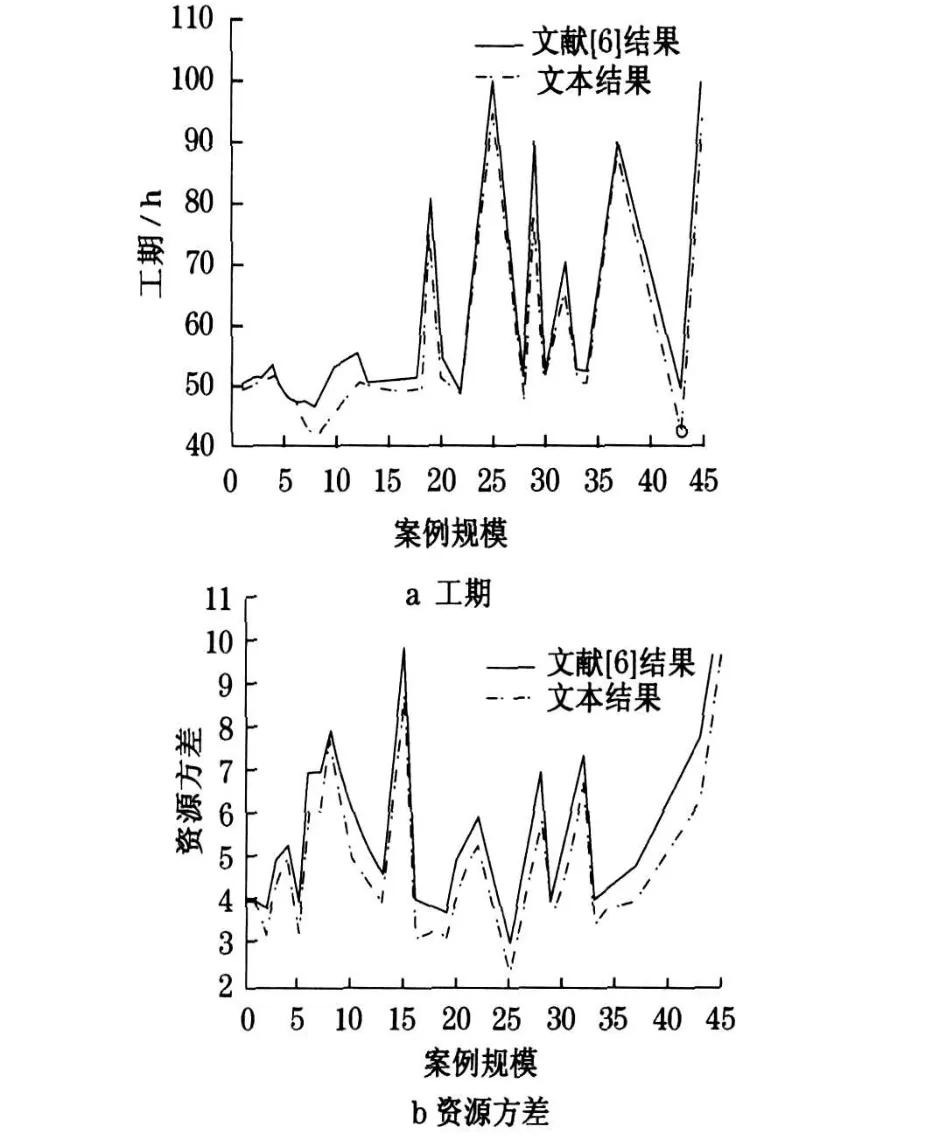
图2 实验工期及资源方差对比Fig.2 Graph of experimental period and resources variance comparison

从表2 可以看出,DMPSO 算法在多目标车辆路径上的应用也是有效的.从Pareto 解的方差来看,得到的Pareto 解集的最优指数和解分布的均匀性都比文献[16] 好, 这是因为DMPSO 算法中拥挤度的衡量在很大程度上提高了解分布的均匀性,同时采用的动态邻域结构在很大程度上也使解之间的信息传送更快、更有效,这也促进了最终得到解的有效性和均匀性.但是DMPSO 算法运行的时间花费比文献[13] 多,主要原因是在计算储备集更新条件和确定动态邻域的过程花费的时间比较多.

表2 文献[16] 和DMPSO算法结果对比Tab.2 Result comparison of reference[16] and DMPSO algorithm

4 结语

给出了一种动态邻域结构的多目标粒子群优化算法,并成功地将此算法应用在一些工程问题中,在储备集更新的过程中, 以支配度和拥挤度的度量为依据,使得解分布的均匀性更优;在粒子搜索的过程中,采用了Gbest 拓扑邻域结构和拟小世界拓扑邻域结构2 种形式, 并依据全局搜索和局部搜索的平衡性来动态调整粒子的拓扑结构.使得粒子的搜索更快,在一定程度上避免了早熟收敛现象.实验结果表明,DMPSO 算法求解多目标优化问题是可行的、有效的.

[1] Leong Yen, Wen Fung,Gary G .PSO-based multiobjective optimization with dy namic population size and adaptive local archives [J] .IE EE Transactions on Sy stem s, Man, and Cybernetics Part B :Cy bernetics, 2008, 38(5):1270.

[2] Brits R,Engelbrecht A P,F .van den Bergh.Locating multiple optimization using particle sw arm optimization[J] .Applied Mathematics and Computation,2007, 189:1859.

[3] Praveen Kumar Tripathi ,Sanghamitra Bandyopadhyay,Sankar Kumar Pal.Multi-objective particle swarm optimization with time variant inertia and acceleration coefficients [J] .Information Sciences,2007, 177:5033..

[4] 张勇, 巩敦卫, 郝国生, 等.含区间参数多目标系统的微粒群优化算法[J] .自动化学报, 2008, 34(8):921.ZH ANG Yong,GONG Dunw ei, H AO Guosheng,et al.Particle sw arm optim ization for multi-objective system with interval parameters[J] .Acta Automatica Sinica,2008, 34(8):921.

[5] 张利彪, 周春光, 刘小华, 等.求解多目标优化问题的一种子群体进化算法[J] .控制与决策, 2007, 22(11):1313.ZH ANG Libiao,ZH OU Chunguang,LIU Xiaohua, et al.Amultiple sub-sw arms evolutionary alg orithm for multiobjective optimization problem s[J] .C ontrol and Decision,2007, 22(11):1313.

[6] 曲红, 吴娟.基于动态多目标粒子群优化算法的资源受限研发项目进度[J] .系统工程, 2007, 25(9):98.Q U H ong,WU Juan.The resource-constrained & project scheduling problem based on dynamic multi-object particle sw arm optimization algorithm[J] .System s Engineering,2007,25(9):98.

[7] 丛琳, 焦李成, 沙宇恒.正交免疫克隆粒子群多目标优化算法[J] .电子与信息学报, 2008, 30(10):2320.CONG Lin, JIAO Licheng,SHA Yuheng .O rthogonal im mune clone particle sw armalgorithm on multi-objective optimization[J] .Journal of Electronics & Information Technology,2008,30(10):2320.

[8] LI Hui,ZH ANG Qingfu.Multiobjective optimization problems with complicated pareto sets, MOEA/ D and NSGA-I[J] .IEE E Transactions on E volution Computation, 2009, 13(1):284.

[9] Tan K C,Yang Y J, Goh C K .A distributed cooperative Coevolutionary algorithm for multi-objective optimization[J] .IEEE Transactions on Evolutionary Computation, 2006, 10(5):527.

[10] Nebro A J, Luna F,Alba E,et al.AbYSS:adapting scatter search to multi-objective optimization[J] .IEEE Transactions on Evolutionary Com putation, 2008, 12(4):439.

[11] Amosa S Bandyopadhyay ,Saha S, Maulik U,et al.A simulated annealing-based multi-objective optimization algorithm [J] .IEEE Transactions on Evolutionary Computation, 2008, 12(3):269.

[12] Carlos A Coello,Coello Pulido Gregorio Toscano, Salazar Maximino, et al .Multiple objectives with particle sw arm optimization [J] . IE EE Transactions on Evolutionary Computation, 2004, 8(3):256.

[13] Kennedy J, Eberhert R.Particle sw arm optimization[C] ∥IEEE International Conference on Neural Networks.Perth :IEEE Press, 1995(1):1942-1948.

[14] James Kennedy,Rui Mendes.Neighborhood topologies in fully informed and best-of-neighborhood particle sw arm s[J] .IEE E Transactions on Systems, Man, and Cybernetics-Part C :Applications and Review s, 2006, 36(4):515.

[15] Clerc M, Kennedy J.The particle sw arm :explosion, stability ,and convergence in a multi-dimensional complex space[J] .IEEE Trans Evol Comput, 2002, 6(1):58.

[16] 徐杰, 黄德先.基于混合粒子群算法的多目标车辆路径研究[J] .计算机集成制造系统, 2007, 13(3):573.XU Jie,H UANG Dexian.Hybrid particle sw arm optimization for vehicle routing problem with multiple objectives [J] .Computer Integrated Manufacturing System s, 2007, 13(3):573.