原地应力状态三维分布估算方法的发展及初步应用＊

Tanno Takeo，Hirano Toru，Matsui Hiroya

1）Crystalline Environment Research Group，Japan Atomic Energy Agency，Japan 2）Crystalline Environment Engineering Group，Japan Atomic Energy Agency，Japan

引言

在地下构筑物的设计中，综合分析原地应力场不仅对设计目的，更对安全建设与施工具有重要意义。一般来说，结构体范围的大小将会决定应力测量方法对原地应力场量化认识的需求程度。然而，想要获得足够的测量值是非常困难的，因为会有多方面的限制，如经费、时间进度和地下结构的尺寸等。

日本原子能机构（Japan Atomic Energy Agency，JAEA）已经提出了一个基于有限应力测量值估算原地应力场的方法。在传统的方法中，只有重力被考虑到原地应力场的计算之中，然而，许多关于原地应力的研究表明[1]，由板块构造力产生的水平应力也应该被考虑到原地应力场的定量研究中去。本文提出了一种考虑由板块构造力引起的水平应力的数值模拟方法，文中介绍了这种方法及其在瑞浪市地下研究实验室（MIU）的原地应力测量中的应用。

1 MIU概述

图1显示了MIU的位置和地质情况。MIU坐落于日本岐阜瑞浪市。MIU选址的调查始于2002年，而对竖井的开挖则开始于同一年的晚期。

MIU测点由两个直径分别为6.5 m和4.5 m的竖井组成。2010年3月的时候，竖井已经达到460 m的深度。它们每隔100 m就通过一个水平段相连接，并在300 m的深度有一个主要水平研究段，计划将增加500 m和1 000 m的主要水平研究段用于地学研究。

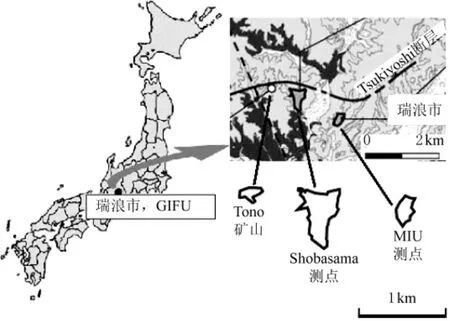
图1 MIU的位置图（据JAEA[2]，有微小改动）

MIU测点附近的地层是由晚白垩纪到早第三纪组成的，基岩花岗岩被180 m厚的第三纪中新世到上新世的沉积岩所覆盖。东-西走向且大倾角的Tsukiyoshi断层使得MIU地区北部的整个地层序列发生了偏移[2]。

2 原地应力场的表达式及数值模拟方法的应用

在方程（1）中，如果“F”和“G”是确定的，那么空间任意一点的应力，即局部应力，可以通过区域应力场计算出来（正演分析）。反过来，区域应力场也可以通过局部应力反演得到（反演分析）。在本研究中，首先通过测量的局部应力定义F或者G，然后通过方程（1）计算区域应力场，进而估算目标区域的原地应力场。

本文分别采用有限元法（finite element method，FEM）和边界元法（boundary element method，BEM）建模。前者考虑了与地质结构相关的不同力学性能的分布，后者考虑了大的不连续面，如Tsukiyoshi断层。

3 非均匀岩层中原地应力分布计算的方法及其应用

3.1 区域应力场的定义

前面我们提到了区域应力场应该考虑由重力和板块构造力双重作用产生的水平应力，前者被定义为由约束边界条件造成的上覆地层压力引起的应力，而后者则是由板块构造力产生的区域应变引起的应力。

其中E和ν分别表示杨氏模量和泊松比。

另外，如果我们考虑由于重力引起的应力，假设密度均匀，那么区域应力可以用方程（3）来表示，这些应力的总和是由于重力和由方程（2）定义的应力共同引起的。

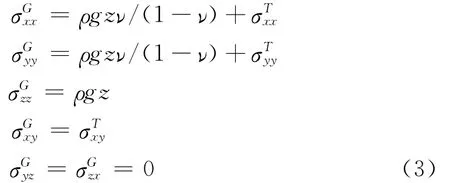
3.2 区域应力场的计算公式

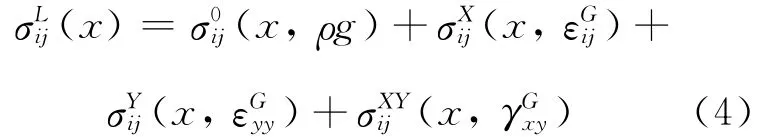
由于线性关系，方程（4）可以改写成方程（5）：

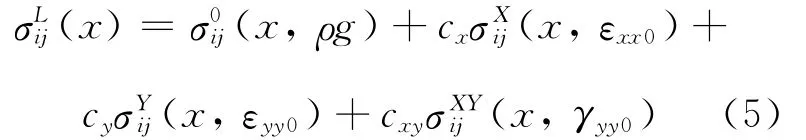
也就是说，如果在分析中为了估算局部应力，我们已经假定εxx0，εyy0和γxy0都是常数的话，我们就能根据方程（6）通过已经测量的应力值的关系估算区域应力。

现在，我们给出观测方程（7）和本构方程（8）。

其中，

用方程（8）估算区域应变对于检测模型参数的敏感性是非常重要的，这是因为估算区域应变既会受到模型形状的影响，也会受到岩石的力学常数的影响。

检测岩石力学常数是特别重要的，如方程（4）中的体积密度、杨氏模量和泊松比。体积密度可以用测试或者密度测井等方法在实验室里精确测量。然而，岩体的杨氏模量和泊松比却因其具有很大的不确定性必须校准。

均方差eA可以用方程（9）来表示；

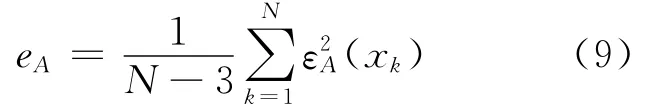
其中，

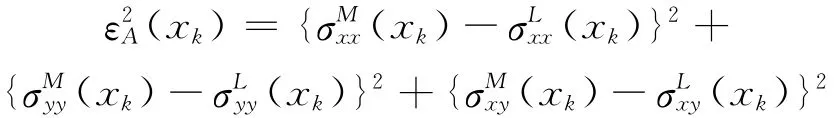
在对模型参数敏感性的测试中，杨氏模量和泊松比在计算eA时的变化是相互制约的，我们使用eA最小时所选取的杨氏模量和泊松比的值来计算原地应力场。

3.3 MIU地区和研究区域应力测量综述

图2显示了应力测量钻孔的位置。5个钻孔在Tono矿山，3个在Shobasama地区的一个3 km×3 km的区域内。钻孔深度范围从几百米到1 km。应力测量采用水压致裂法，原地应力测量在每个测孔不同深度进行测量，测点共有90个。

为了构建三维力学模型来反应地质结构和钻孔测量的结果[3]，我们将岩层分为4层，第Ⅰ层到第Ⅳ层的厚度如图3所示。体密度值的选取基于实验室的测量和密度测井方法所得到的数据。

岩体的杨氏模量和泊松比是未知量，杨氏模量被定义成特殊的杨氏模量E4，因此，在研究中，我们共有3个未知量，E1/E4，ν1和ν4。

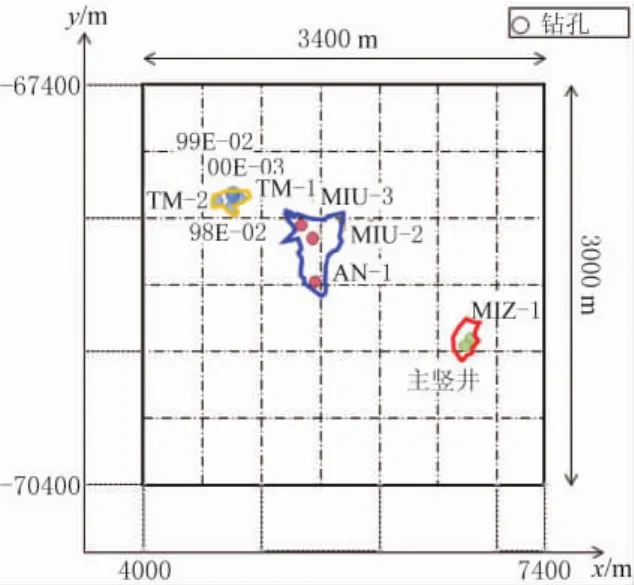
图2 研究区域

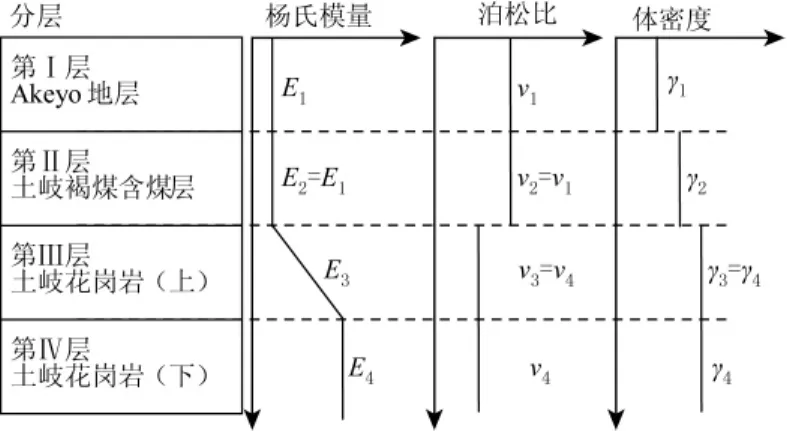
图3 地质和岩石力学性质

3.4 区域应力场的计算

三维有限元模型结构如图4所示，模型大小是3.4 km×3 km×大约1 km，我们将在这个范围内估算区域应力。数值模拟方法用的是有限元法，模型由六面体单元组成，平面单元大小是20 m×20 m，垂向单元个数是25个，总单元数和节点数分别是637 500和671 346。

接下来，我们估算MIU地区的区域应力场并检查特殊杨氏模量E1/E4和泊松比ν1和ν2的效果，这些数据都基于Tono和Shobasama测点的应力测量值。岩石力学常数的敏感性分析结果见图5所示。

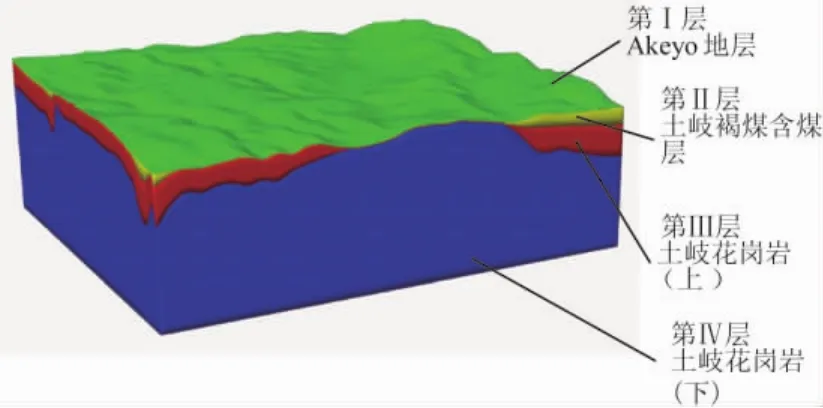
图4三维有限元模型（3.4 km×3 km×大约1 km）

在图5中，当E1/E4＝0.1，ν1＝0.4且ν4＝0.3时均方差最小，也就是说，这种取值组合给出了最优解。这个结果也与实验室对岩石样品的测试结果相一致。

同样地，计算出来的区域应变（×10－3）是＝－0.351，＝－0.437。此时，实验室测量的杨氏模量E1和E4的估值分别为2 GPa和20 GPa。

3.5 MIU原地应力场的估算

利用3.4节计算出来的区域应力场，我们计算MIU地区的原地应力场，并与使用测量值估计出来的应力场进行比较。

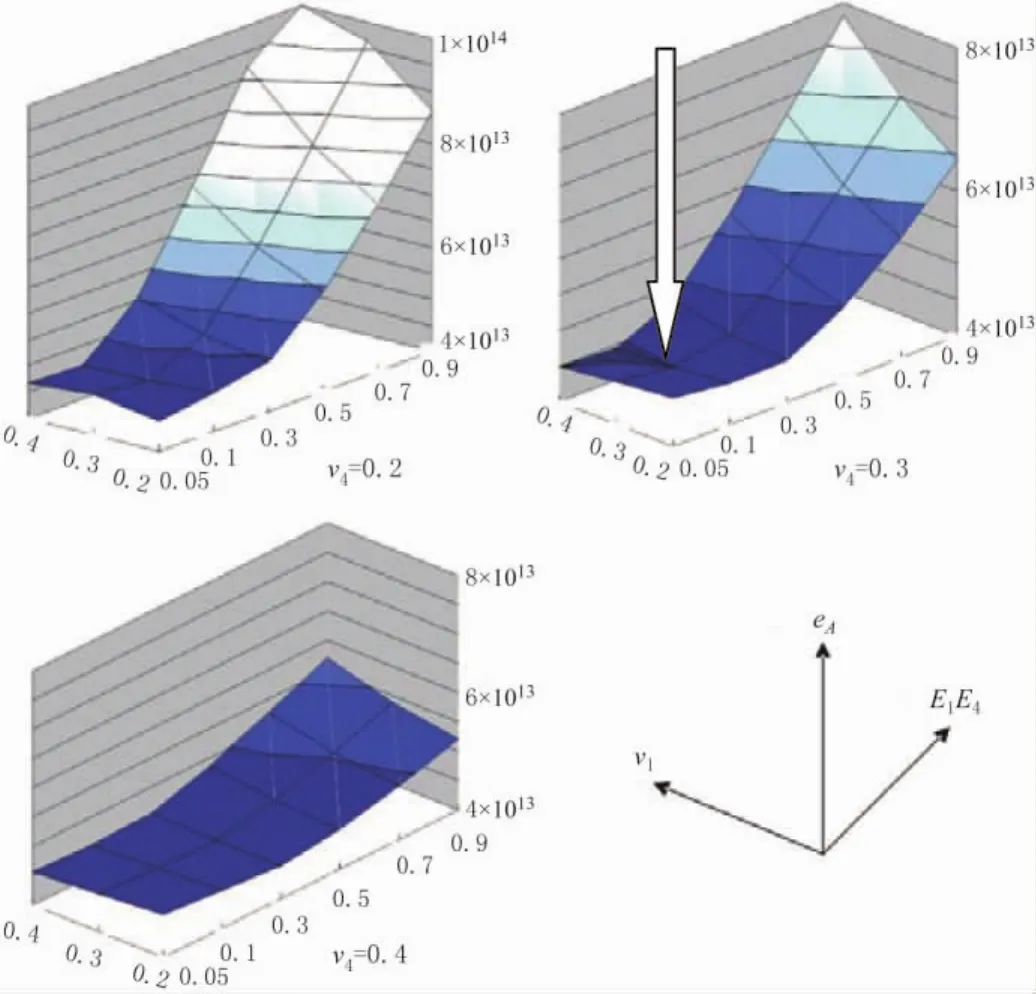
图5 利用特殊杨氏模量E 1/E 4和体密度及ν1和ν4进行敏感性分析的结果

另外，在MIU地区钻探的“MIZ-1”钻探中的原地应力测量值已经测出，而100 m和200 m的原地应力测量值也在进行中。MIU地区原地应力测量值与MIU地区原地应力计算结果的比较见图6。

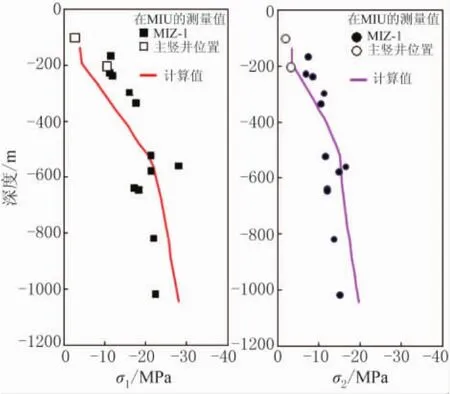
图6 MIU地区测量值与计算值的比较

测量与计算得到的应力值在量级上有小的区别，但其随深度的变化却颇为相似，尤其是在600 m深度时的变化趋势。

4 非线性组成的大的不连续体中原地应力分布的计算方法及其应用

4.1 区域应力场的定义

区域应力场用方程（10）来定义。这个定义给出了应力分量由于板块构造力而随深度非线性变化的情况，除了方程（3）中的由重力引起的应力分量。

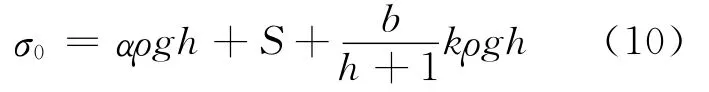
其中，

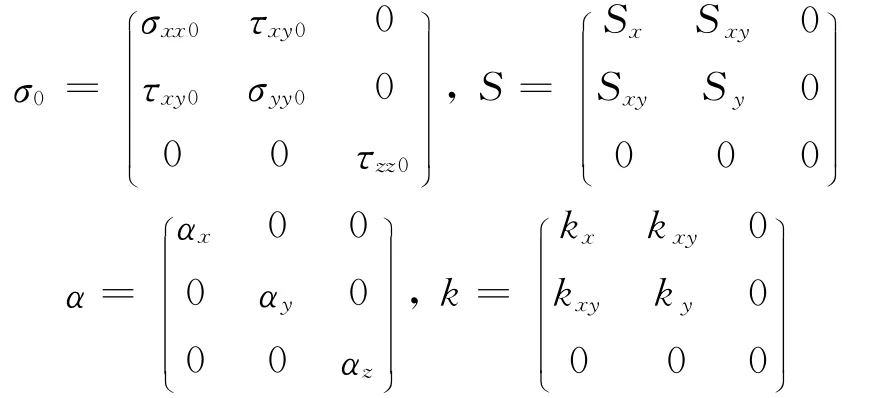
其中，σ0是深度h的区域应力，α是重力引起的矩阵，αx＝αy＝ν/（1－ν），αz＝1，S则是不随深度变化的常应力值。每个a，b和k值都是表示水平板块构造应力的非线性参数。

4.2 区域应力场的计算

4.2.1 非均匀模型中边界元法分析程序的发展

边界元法具有适用于无限大的块体的优点，但是，它不可能应用到具有不同参数的非均匀介质模型上。

因此，我们发展了一套新的数值模拟程序来处理非均匀模型。

4.2.2 原地应力分布的估算方程

如果i点的局部应力为（σci），则（σci）可以表示为方程（11）：

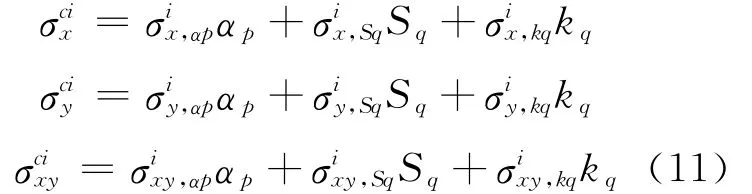
其中，p＝x，y，z q＝x，y，xy。

如果i点的应力测量值记作（σmi）（i＝1～N），它可以表示为方程（12），观测方程由方程（13）定义。

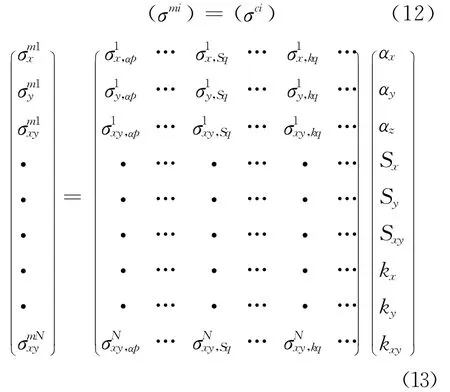
因为αx，αy和αz都是由泊松比决定的，未知量就有6个：Sx，Sy，Sxy，kx，ky和kxy，区域应力场使用最小二乘法来估算这些未知量。

4.3 分析区域和应力测点的模型

本节用来分析的应力数据与第3部分相同，模型被分为两层，上层是砂岩和泥岩的沉积岩相，最大厚度150 m，下层是巨大的土岐花岗岩。这个模型包含一个大的不连续体，即Tsukiyoshi断层。将此断层简化为一个东西走向且倾角为60°倾向朝南的平面。

4.4 区域应力场的计算

该模型采用边界元法（BEM）（图7）。模型在水平面的尺寸是3.2 km×2.4 km，垂向大概1 km。单个元素在水平面的尺寸是200 m×200 m。Tsukiyoshi断层采用位移不连续方法（Displacement Discontinuity Method，DDM）建模。

首先，根据测量的应力数据使用单纯性方法计算出方程（10）中的两个常数a＝904.6，b＝812.1。然后用最小二乘法估算区域应力场[方程（12）]。表1是估算出的区域应力场。

4.5 MIU地区的原地应力场估算

利用4.4节计算的区域应力场，我们计算了MIU地区的原地应力场，与通过测量数据估算的应力场进行比较。原地应力场的计算被应用于采用有限差分法进行进一步的分析中（图8）。

图9给出了测量结果与MIU地区计算出的原地应力的比较，可以看出，计算值与测量值几乎没有不同。计算值基本上是随深度增加，且增加的趋势与测量值保持一致。计算值甚至在穿过土岐花岗岩的时候出现波动，而这里应该是均匀的介质，所以我们认为这是因为模型中包含断层的原因。

图7 边界元模型

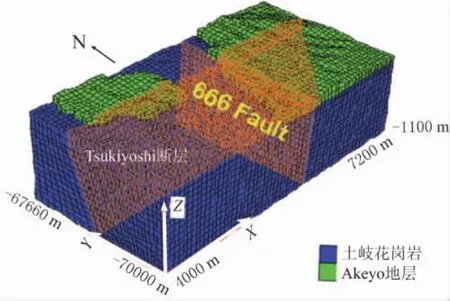
8 有限差分法模型

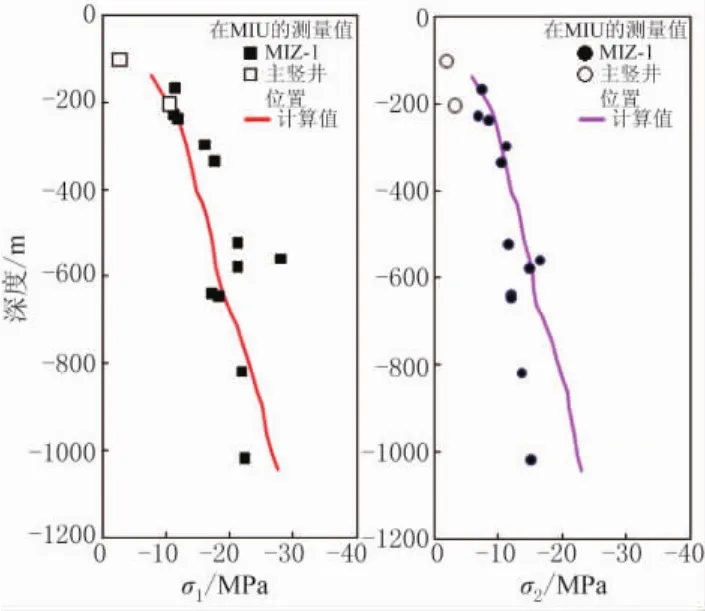
图9 MIU地区应力测量值和计算值的比较

5 结论

在本研究中，我们以地下结构区域中有限的应力测量值为基础，给出了两种不同的数值模拟方法来估算原地应力场。在传统方法中，对原地应力随深度变化主要趋势的估算只考虑了重力的因素。然而，我们提出的数值模拟方法可以考虑因板块构造力引起的水平应力在内的局部应力的变化。

第3部分构建了一个地质模型，模型将基岩根据地质情况分成4层并赋予不同的岩石力学性质。通过这种方法，我们可以确定用于估算模型区域应力场的最优岩石力学参数值。在第4部分，我们改进了普通的BEM程序，使其能够适用于真实的地质结构和大的不连续体。然后，将改进的数值模拟程序应用到区域应力计算中，而原地应力场的估算则使用了比有限差分更进一步的分析方法。

表1 计算出的区域应力场

结果表明，第3部分提到的对非均匀岩体的建模的有限元方法，比起第4部分提到的BEM方法，能更准确地估算应力值。然而，考虑大的不连续性是非常重要的，因为它能影响原地应力场。另外，建立模型的方法论也是很重要的。

以后还将给出更深地区的应力测量值与MIU地区原地应力计算值进行比较。此外，随着对MIU地区的继续研究，可以得到更多的力学和地理参数，我们将在这些数据的基础上改进三维模型，而且将进一步研究大的不连续性对估算原地应力场的影响。

[1]Sulistianto B，Kido T，Mizuta Y.Determination of far field stress from the point stress measurement.Shigento to Sozai，1998

[2]JAEA.Final report on the surface-based investigation（phase 1）at the Mizunami underground laboratory project.2007

[3]JAEA.The result of the geomechanical investigations in the MIU-3 borehole and the conceptual geomechanical model of the Toki granite in Shobasama area：JNC TN7420 2001-001.2000