关于r次可加补数的一些复合函数的均值性质*
金 晶, 朱伟义
(浙江师范大学数理与信息工程学院,浙江金华 321004)
0 引言
定义[10]设r≥2为任意给定的正整数.一完全r次幂的最小非负整数,则称可加补数,即


1 预备知识
首先给出一些主要结果证明中需要用到的引理.
引理1[1]设k为给定的正整数,则对任意的实数x>1,有渐近公式

引理5 设h(n)为非负的算术函数,且h(0)=0,给定正整数r≥2,则对任意实数x≥1,有渐近公式

其中:


引理5证毕.
2 主要结果
定理1 设k为给定的正整数,则给定正整数r≥2,对任意实数x≥2,有渐近公式

证明 对任意的实数x≥2,设M为一个固定的正整数,且满足

因为

因此,

所以,结合式(5)和式(6)可得

由式(4)和式(7)可得

定理2 设k为给定的正整数,则给定正整数r≥2,对任意实数x≥2,有渐近公式

证明 类似于定理1的证明,根据ar(n)和V(n)的定义及引理5,并利用估计式V(n)≪nε(ε为任一固定的正数),得

由式(8)和式(10)可得

定理3 给定正整数r≥2,对任意实数x≥1,有渐近公式


结合式(6)和式(12)可得
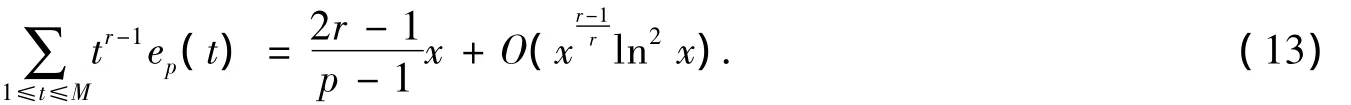
由式(11)和式(13)易知

定理3证毕.
[1]薛教社.一个新的算术函数及其均值[J].纯粹数学与应用数学,2007:23(3):351-354.
[2]沈虹.一个新的数论函数及其它的值分布[J].纯粹数学与应用数学,2007,23(2):235-237.
[3]Lü Chuan.A number theoretic function and its mean value[M]//Zhang Wenpeng.Research on Smarandache problems in number theory.Phoenix:Hexis,2004:33-36.
[4]马金萍.k次幂部分剩余函数的均值[C]//杨晓虎,程国建,王佐仁.第十二届中国青年信息与管理学者大会论文集.西安:中国运筹学会,2010:57-59.
[5]Florentin.Only problems,not solutions[M].Chicago:Xiquan Publishing House,1993:26.
[6]朱伟义.关于整数 n 的 k次补数[J].数学学报,2005,48(4):817-819.
[7]Zhu Weiyi.On the k-power complement and k-power free number sequence[J].Smarandache Notions Journal,2004,14(1):66-69.
[8]Liu Hongyan,Lou Yuanbing.A note on the 29-th Smarandache's problem[J].Smarandache Notions Journal,2004,14(1):156-158.
[9]Yao Weili.On the k-power complement sequence[M]//Zhang Wenpeng.Research on Smarandache promblems in number theory.Phoenix:Hexis,2004:43-46.
[10]Xu Zhefeng.On the additive of k-th power complements[M]//Zhang Wenpeng.Research on Smarandache promblems in number theory.Phoenix:Hexis,2004:13-16.
[11]Ding Liping.On the additive k-power complements[M]//Zhang Wenpeng,Li Junzhuang,Liu Duansen.Research on Smarandache promblems in number theory.Phoenix:Hexis,2005:23-27.
[12]Guo Yanchun.On the additive k-power complements[J].Scientia Magna,2008,4(2):4-7.
[13]Tom M A.Introduction to analytic number theory[M].New York:Springer-Verlag,1976.

