IPF算法与N-R算法的对比研究及应用

李春红，黄绍军，廖娟芬

（广西大学 数学与信息科学学院，广西 南宁 030051）

IPF算法与N-R算法的对比研究及应用

李春红，黄绍军，廖娟芬

（广西大学 数学与信息科学学院，广西 南宁 030051）

IPF算法和N-R算法在列联表的相关模型研究中应用广泛.本文通过MATLAB实现了IPF算法和N-R算法，并通过数据模拟研究了两种算法的优劣.模拟结果显示，IPF算法具有稳健、简洁等特点，而N-R算法在迭代次数、精度方面有优势，算法的实现和对比研究对实际应用具有重要地参考意义.

列联表；IPF算法；N-R算法

联表在医学、生物学、工农业和社会科学等有着广泛的应用，引起人们不断地去研究，提出了对数线性模型、Logistic回归模型和多元分析模型等多种模型[1].这些分析模型应用到高维列联表时，可以把高维列联表划分为独立模型和相关模型[2]，对于独立模型可以直接用观测数据进行估计，而相关模型则不能直接用观测数据来估计，于是人们提出了各种迭代算法.常用的算法有，迭代比例拟合算法（Iterative Proportional Fitting Algorithm，IPF）[2-3]和牛顿—勒夫逊算法（Newton-Raphson，N-R）[1].文献[2]用分别IPF算法和N-R算法，文献[3]提出了IPF算法对三维列联表进行拟合，文献[4]给出了在对高维列联表进行探索性分析时IPF算法比较简单、稳健，但并没有深入的对这两种算法进行比较分析.本文利用Matlab对两种算法进行模拟，通过比较分析，阐明了IPF算法与N-R算法的优劣性．

1 算法简介

假设有n个个体根据三个属性X、Y和Z进行分类.属性X有r类，记为X1，…，Xr，属性Y有c类，记为Y1，…，Yc，属性Z有t类，记为Z1，…，Zt.n个个体中属于Xi、Yj和Zk类的有nijk个，比如表1中，n111=22，根据这三个属性绘制一个交叉表，就得到一张三维的r×c×t列联表.例如在研究手术后并发症是否与手术类型有关的课题中，得到见表1.

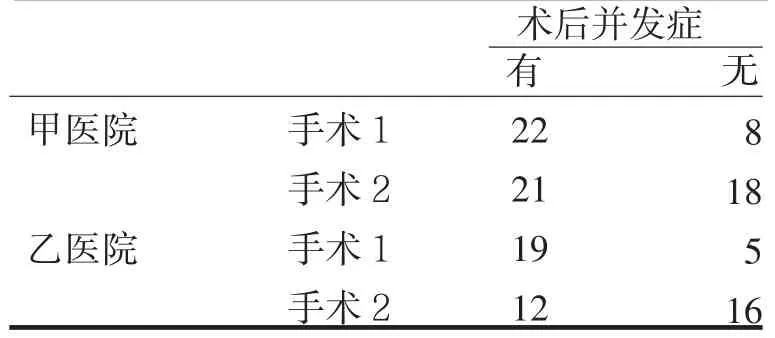
表1 并发症与手术类型案例数据Fig.1 Cases of complications with operation types

这就是一张2×2×2三维列联表.实际上，属于Xi、Yj和Zk类的个体是以一定值的概率发生，其概率值记为Pijk.那么于全部个体n，属于Xi、Yj和Zk类的理论个数为npijk，该理论值称为期望频数，记mijk=npijk.对应的，实际属于Xi、Yj和Zk类的个数nijk称为实际频数，并且有Enijk=mijk.

如果两个属性X和Y之间毫无关系，就称X和Y相互独立，反之就称X和Y相关.在列联表中，如果两个属性X和Y之间存在相关关系，就称X和Y之间有二次交互作用，如果两个属性X、Y和Z之间存在相关关系，就称X、Y和Z之间有三次交互作用．

三维列联表的相关模型有两种.一种是饱和模型，其期望频数不能分解，此模型三个属性X、Y和Z不仅两两之间有交互作用，而且三个之间也有交互作用，其期望频数的估计值就是实际频数；另一种是期望频数可以分解，此模型三个属性X、Y和Z仅两两之间有交互作用，但三者之间没有交互作用.可分解模型可记为mijk=αijβikγjk，其中αij、βik和γjk分别表示（X，Y）、（X，Z）和（Y，Z）之间交互作用，可分解相关模型的期望频数的估计值要求用迭代算法来估计，常用的有IPF算法和N-R算法.下面就这两个算法进行简单介绍．

1.1 IPF算法简介

对于可分解相关模型mijk=αijβikγjk，求其极大似然估计有代估计就是期望频数mijk的极大似然估计mijk．

1.2 N-R算法简介

N-R算法是求解非线性方程组的常用方法，对于相关模型mijk=αijβikγjk同样可以通过N-R算法来估计.相关模型 mijk=αijβikγjk中含有的独立参数个数可以通过对数线性模型变换来体现，其对数线性模型的表达如下：

2 数据模拟

本文通过Matlab数学软件进行数值模拟.模拟分为两部分，第一部分求N-R算法的有效区间，第二部分是模拟比较两种算法.第二部分模拟了100次，模拟过程分为三步骤进行，第一步由Poison分布随机生成一个三维的列联表，第二步分别IPF算法和N-R算法对列联表进行数值计算，第三步对计算结果进行组合整理后输出数值结果.模拟具体过程如下.

2.1 求解有效区间的算法代码及输出结果

说明，Meandx为平均有效区间的输出结果，即N-R算法的平均有效区间为(β0-0.4089,β0+3.8890),β0为初始值.

2.2 IPF算法与N-R算法模拟比较的代码及输出结果

说明，Meanlter、SumOutChi、SumOutLh 都是结果输出.Meanlter中6.3000是N-R算法的平均迭代次数，8.9200是IPF算法的平均迭代次数；SumOut⁃Chi是两种算法通过卡方检验值比较得出的计算结果，输出结果有6个元素，分别表示为，①模拟无效个数；②IPF卡方检验值大于N-R卡方检验值的个数；③卡方检验值相等的个数；④IPF卡方检验值小于N-R卡方检验值的个数；⑤卡方检验值的差值总和；⑥卡方检验值差值比率的总和（以N-R值为基数），即对应的结果为[0 94 0-6 139.5953 0.2380]；同样，SumOutLh是两种算法通过似然比值比较得出的计算结果，其各个元素的代表的意义跟SumOutChi一样.

3 结果分析

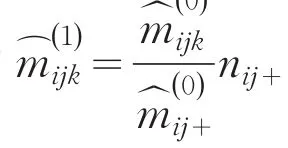
即只要初始值不为零且相等，就进行迭代运算．

2）从迭代次数来看，IPF算法平均迭代次数为8.9200，N-R算法在β0处的平均迭代次数为6.3000.由此我们可以看出，N-R算法的迭代次数在初始值β0出具有较强的收敛速度．

3）从检验值的比较来看，IPF算法的似然比值大于N-R算法似然比值所占的比率为99%，IPF算法的似然比值小于N-R算法所占的比率为1%，而且IPF算法的似然值比N-R算法似然比值差值比率的平均值为0.9471%，可见N-R算法比IPF算法在似然比值的标准下有优势.同样的，通过卡方检验值来比较也得出相同的效果．

4）如果要应用到实际的数据，去掉生成矩阵A的函数，把A设定为主函数输入参数即可.对于N-R算法，当有的观测值为0时，有可能不收敛，所以建议把观测值都加上0.5再进行运算．

4 小结

本文通过Matlab来对比分析IPF算法与N-R算法，得出了IPF算法具有稳健、简洁等特点，而N-R算法在迭代次数、精度方面有优势.就拟合结果来看，IPF与N-R算法分析结果基本上一致，但N-R的能够详细的给出参数的估计值，因此本文提倡用N-R算法.另外，对于SAS、SPSS等统计软件不熟悉的科研工作者，可以参考利用本文代码在Matlab上进行数值求解．

[1]张尧庭,夏立显,安希忠,等.定性资料的统计分析[M].广西:广西师范大学出版社,1991:78-85.

[2]王静龙,梁小筠.定性数据统计分析[M].北京:中国统计出版社,2008:147-155.

[3]Santner T J,Duffy D E.The Statistical Analysis of Discrete Data[M].New York，Spring-Verlag,1989:113-199．

[4]张岩波,何大卫.对数线性模型的IPF算法及其软件实现[J].中国卫生统计,1999,16(5):258-259．

Comparative Analysis and Application of IPF Algorithm and N-R Algorithm

LI Chunhong,HUANG Shaojun,LIAO Juanfen
（College of Mathematics and Information Science，Guangxi University，Nanning530004，China）

IPF algorithm and N-R algorithm are widely used in the dependence modeling of contingency table.This ar⁃ticle wrote IPF algorithm and N-R algorithm codes in the MATLAB Software and compared the two algorithms by means of digital simulation.The simulation showed that IPF algorithm hold the robustness and briefness features,N-R algo⁃rithm had advantages in iterations and precision.The codes and conclusion offered important reference value in practical application.

contingency table；IPF algorithm；N-R algorithm

O 212.1

A

1674-4942（2011）02-0128-03

2011-01-25

国家自然基金资助项目（11061002）

毕和平