一个新的极小谱任意复符号模式矩阵

张晓婷，高玉斌

（中北大学 数学系，山西 太原 030051）

一个新的极小谱任意复符号模式矩阵

张晓婷，高玉斌

（中北大学 数学系，山西 太原 030051）

若给定任意一个n阶首1复系数多项式 f(λ)，都存在一个复矩阵B∈Q(A) ，使得的特征多项式为 f(λ)，则称n×n复符号模式矩阵A是谱任意的.如果A是一个谱任意复符号模式矩阵且A的任意真子模式都不是谱任意的，那么A是一个极小谱任意复符号模式矩阵.本文扩展了N-J方法证明了一个的复符号模式矩阵是极小谱任意的n≥4.

复符号模式；蕴含幂零；谱任意模式；极小谱任意

对任意给定的的实数a，我们用sgn（a）表示其符号，根据a＞0，a＜0分别定义其符号为1，-1和0.元素取自于{1，-1，0}的矩阵称为符号模式矩阵.对于给定的实矩阵B，由其每个元素符号所组成的矩阵称为B的符号模式矩阵，记为sgn（B）.用Qn表示全体n阶复符号模式矩阵组成的集合.对任意A∈Qn，所有与A有相同符号模式的复矩阵组成的集合{B |sgnB=A} 称为A所决定的定性矩阵类，记为Q（A）.

若A=（ak）l和B=（bk）l是两个n×n符号模式矩阵，如果当bkl≠0时，akl=bkl，则称A是B的母模式，也称B是A的子模式.每个符号模式是其本身的母模式和子模式.若B是A的子模式，且B≠A，则称B是A的真子模式.

设A=（ak）l和B=（bk）l是两个符号模式矩阵，则称S=A+iB为n阶复符号模式矩阵，其中i2=-1.显然skl=akl+ibkl，k，l=1，2，…，n.所有与S有相同符号模式的复矩阵组成的集合称为S所决定的定性矩阵类.记为

Qc(S)={C =A+iB|sgn(A)=A,sgn(B)=B}其中A，B为n×n实矩阵.

若S1=A1+iB1和S2=A2+iB2是两个n×n复符号模式矩阵，如果A1是A2的子模式，且B1是B2的子模式，则称S1是S2的子模式，也称S2是S1的母模式.若S1是S2的子模式，且S1≠S2，则称S1是S2的真子模式.若S=A+iB是n阶复符号模式矩阵，符号模式矩阵A和B分别为S的实部和虚部，则A和B的所有非零元的个数即为S的非零元的个数.

设S=A+iB是n≥2阶复符号模式矩阵，如果复数矩阵C∈QC(S)的特征多项式是 f(λ)=λn，则称S是蕴含幂零的，C是幂零复矩阵.一个复符号模式矩阵S是谱任意的，当且仅当对给定的任意一个次首1复系数多项式 f(λ)，都存在QC(S)中的一个复矩阵，使得它的特征多项式为 f(λ).如果S是一个谱任意复符号模式矩阵，且S的任意真子式都不是谱任意的，则S是一个极小谱任意复符号模式矩阵.

1 N-J方法

谱任意符号模式的概念最早是在文献[1]提出的，并且给出了运用N-J方法证明一个实符号模式及其它的母模式都是谱任意的.在文章[2]中提出了著名的2n猜想，即任意不可约谱任意符号模式矩阵至少有2n-1个非零元.文章[3]中对ray模式的谱任意性进行了讨论,

将N-J方法推广到ray模式，并且给出了一类谱任意ray模式.文章[4-7]中对复符号模式的谱任意性进行了研究，将N-J方法推广到复符号模式，对复符号模式谱任意的研究有重要的意义..

引理1S=A+iB是n≥2阶复符号模式矩阵，且至少有2n个非零元.

1）在复符号模式矩阵类QC()S中找一个幂零复矩阵C=A+iB，其中A和B为实矩阵，且A∈Q(A),B∈Q(B).

2）将A和B中的2n个非零元（记为r1，r2，…，r2n），替换为变量t1，t2，…，t2n.

3）替换后的矩阵的特征多项式表达如下：

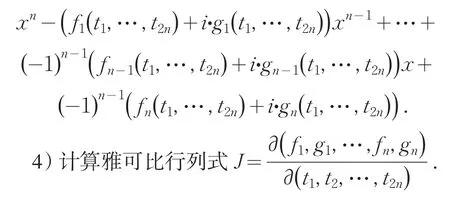
5）如果雅可比行列式J在幂零点（t1，t2，…，t2n）=（r1，r2，…，r2n）处不等于零，则S的任意母模式是谱任意的.

2 主要结果

本文主要讨论下面的n阶（n≥4）符号模式

其中ai，bk为正实数，j=1，…，n，k=1，…，n.

下面先给出一个非零实多项式的零点的定义（有限次）.如果ft是一个非零实多项式，令

若Zf是非空的，则Zf的最大值记为max( )Zf.若Zf是空的，则记为max(Zf)=-∞.

下面将用∂(f)来表示多项式 f(t)的次数.

[1]Drew J H,Johnson C R,Olesky D D.Pvan den Driess⁃che,Spectrally arbitrary patterns[J].Linear Algebra and its Applications,2000,308:121-137.

[2]Britz T,McDonald J J,Olesky D D.Pvan den Driessche,Minimal spectrally sign patterns[J].SIAM Journal on Ma⁃trixAnalysis and Applications,2004,26:257-271.

[3]McDonald J J,Stuart J.Spectrally arbitrary ray patterns[J].Linear Algebra and its Applications,2008,429:727-734.

[4]Gao Y B,Shao Y L,Fan Y Z.Spectrally arbitrary complex sign pattern matrices[J].Electronic Journal of Linear Alge⁃bra,2009,18:674-692.

A New Matrix of Minimally Spectrally Arbitrary Complex Sign Patterns

ZHANG Xiaoting，GAO Yubin
（Department of Mathematics，North University，Taiyuan030051，China）

A complex sign pattern matrixAof order n is a spectrally arbitrary pattern if given any monic polynomialf（λ）with coefficients fromCof order n,there exists a complex matrixBinQ（A）such that the characteristic polynomial ofBisf（λ）.IfAis a spectrally arbitrary complex sign pattern matrix,and no proper subpattern ofAis spectrally arbi⁃trary,thenAis a minimal spectrally arbitrary complex sign pattern matrix.In this paper,we extend the Nilpotent-Jacobi⁃an method to prove a complex sign pattern matrix is minimally spectrally arbitrary pattern for all ordersn≥4.

Complex Sign pattern；Potentially nilpotent；Spectrally arbitrary pattern；Minimally spectrally arbitrary

O 151.21

A

1674-4942（2011）02-0119-04

2010-12-27

国家自然基金项目（11071227）；山西省自然科学基金资助项目（2008011009）

毕和平