构造奇数阶对称幻方及奇偶分开对称幻方的新方法

詹 森，王辉丰

（1.广东技术师范学院 计算机科学系，广东 广州 510665；2.海南师范大学 数学与统计学院，海南 海口 571158）

构造奇数阶对称幻方及奇偶分开对称幻方的新方法

詹 森1，王辉丰2

（1.广东技术师范学院 计算机科学系，广东 广州 510665；2.海南师范大学 数学与统计学院，海南 海口 571158）

用匹配两步法构造出奇数n=2m+1（m为自然数）阶对称幻方，用匹配余函数两步法构造出奇数n阶奇偶分开对称幻方，具有普遍性，并给出了证明.这些方法可分别得到2m(m !)·2m-1(( m-1)!) 个不同的n阶对称幻方；当n=2m+1（m=2k，k=1，2，…）时，可构造出2m(k !)·2m-1(k!)(( k-1)!) 个不同的n阶奇偶分开的对称幻方；当n=2m+1（m=2k+1，k=0，1，2，…）时，可构造出2m(( k+1)!)(k!)·2m-1(k!)2个不同的n阶奇偶分开的对称幻方.

对称幻方；奇偶分开对称幻方；匹配基数；余函数

我们在文[1]中讨论了构造奇数n=2m+1（m为自然数）阶对称幻方、奇偶分开对称幻方的两步法，其基数的安装具有以下局限性：从左到右是按由小到大的顺序进行的，基数下方、上方元素的安装是按自然数的顺序安装；只能构造出一个n阶对称幻方或一个n阶奇偶分开对称幻方.然而，这方法给出了通项公式，为克服上述局限性奠定了基础.在此基础上，我们下面将利用匹配基数和文[2]的余函数进一步研究以上两类幻方的构造方法，得到新的更好的更一般的结果.

1 奇数n=2m+1（m为自然数）阶对称幻方的构造法

我们已知n阶基方阵A[2]的基数共有n个，它们是

1，n+1，2n+1，…，（m-1）n+1，mn+1，（m+1）n+1，…，（n-1）n+1.值得注意的是，基数k·n+1与（n-1-k）n+1（k=0，1，…，n-1但k≠m）之和都等于（n-1）n+2，这样的一对基数叫做匹配基数.这是不同于文[1]之处.而把第j列与笫n-j+1列（j=1，2，…，n）叫做对称列.

第一步 安装基方阵.

设n=2m+1（m=1，2，…）阶基方阵[2]A位于第i行、第j列的元素为a（i，j）（i，j=1，2，…，n），将基数按如下方式安装到n阶方阵A中，取定a（1，m+1）=mn+1，其余n-1个基数

1，n+1，2n+1，…，（m-1）n+1，（m+1）n+1，…，（n-1）n+1，

可随意安装到如下n-1个位置：

a（m+1-k，k+1））（k=0，1，2，…，m-1），

a（m+1+k，n-k+1）（k=1，2，…，m）.

但匹配基数必须置于对称列中，安装于第j列的基元记作ncj+1（j=1，2，…，n），基数安装完毕后，得到方阵A的全部基元（或站点）.

取定d1=1，dm+1=m+1，dn=n，注意到1～n的自然数列中处于中心对称位置上的两个自然数，其和都等于n+1，除d1=1和dn=n外，我们共有m-1对这样的自然数，在每对自然数中随意选取一个自然数，将这m-1个自然数随意排序依次记为dk（k=2，3，…，m）；余下的m-1个自然数记为dn-k+1（k=2，3，…，m），但必须满足条件dk+dn-k+1=n+1（k=1，2，…，m）.在第j列基元ncj+1的下方（包括该基元），自上而下按ncj+dk（k=1，2，…，n）的顺序安装相继的数至该列最下面的笫n行；接着，在该站点的上方，自上而下按该顺序安装后继的数，安装至全列满为止.所得到的n阶方阵叫做基方阵A，基方阵A的每一行数字之和都等于幻方常数且中心对称位置上两个数的和都等于n2+1.

第二步 对基方阵施行顺移，安装到另一个（待安装的）n阶方阵B.

把A中第一列每一行的数字移至同一行相应于A的基数所在的位置，同一行其他数字顺移，当各行都完成了这一程序之后，所得方阵B就是一个对称幻方.

上述方法改进了[1]的两步法，具有更普遍性.我们称之为构造奇数阶对称幻方的匹配两步法.对于给定的n=2m+1（m=1，2，…），匹配两步法可构造出2m(m !)·2m-1(( m-1)!)个不同的n阶对称幻方（不包括由于对称行或列对调而衍生的n阶对称幻方）.

定理1 用匹配两步法构造的n=2m+1（m=1，2，…）阶方阵B是对称幻方.

证明 由文[3]的定理1证明知，基方阵A位于第i行、第j列的元素a（i，j）为

即B是关于中心对称的方阵，故方阵B是一个n阶对称幻方.定理证毕.

（注意：由文[3]的定理1证明知，对n=2m+1=2（3t+1）+1=6t+3（t=0，1，2，…）需取dk=k（k=1，2，…，n）才能保证方阵B是一个n阶对称幻方）.

2 奇数n=2m+1（m为自然数）阶奇偶分开的对称幻方的构造法

奇数集中于方阵中央的菱形中而偶数置于方阵四角的n阶对称幻方，叫做n阶奇偶分开的对称幻方.现在对n阶奇偶分开的对称幻方的构造方法讨论如下：

第一步 安装基方阵.

设n=2m+1（m=1，2，…）n阶基方阵A位于第i行、第j列的元素为a（i，j）（i，j=1，2，…，n），将基数按如下方式安装到n阶方阵A中，取定a（1，m+1）=mn+1，其余n-1个基数是1，n+1，2n+1，…，（m-1）·n+1，（m+1）n+1，…，（n-1）n+1，可随意安装到如下n-1个位置：

a（m+1-k，k+1））（k=0，1，2，…，m-1），

a（m+1+k，n-k+1）（k=1，2，…，m）.

但匹配基数必须置于对称列中，且笫一列取奇基数，然后从左到右奇基数与偶基数相间隔.安装于第j列的基元记作ncj+1（j=1，2，…，n），基数安装完毕后，得到方阵A的全部基元（或站点）.

取定d1=1，dm+1=m+1，dn=n，注意到1～n的自然数列中处于中心对称位置上的两个自然数（除d1=1和dn=n外），其和都等于n+1，我们共有m-1对这样的自然数，在每对自然数中随意选取一个自然数，将这m-1个自然数随意排序依次记为dk（k=2，3，…，m）；余下的m-1个自然数记为dn-k+1（k=2，3，…，m），但必须满足条件dk+dn-k+1=n+1（k=1，2，…，m）.且k为奇数时dk为奇数，k为偶数时dk为偶数，奇偶数相间隔.在第j列基元ncj+1的下方（包括该基元），自上而下按ncj+dk（k=1，2，…，n）的顺序安装相继的数至该列最下面的笫n行；接着，在该站点的上方，自上而下按该顺序安装后继的数，安装至全列满为止.所得到的n阶方阵叫做基方阵A.

由文[3]的定理1证明知，基方阵A位于第i行、第j列的元素a（i，j）为

a（i，j）=ncj+dr（m+（i+j））（i，j=1，2，…，n）.其位于中心对称位置上的元素为

即基方阵A的每一行数字之和都等于幻方常数且中心对称位置上两个数的和都等于n2+1.

第二步 对基方阵A施行顺移，安装到另一个（待安装的）n阶方阵B.

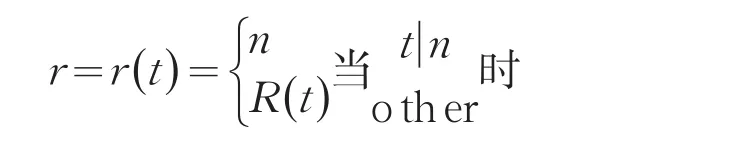
我们将利用文[2]定义的余函数对基方阵A进行安装，这个余函数为这里，t是自然数，t|n是表示t被n整除，other是指其他情况，R（t）是表示t除以n的余数.

基数a（m+1-k，k+1）（k=0，1，2，…，m-1）所在行的元素向右顺移r（k·m）（k=0，1，2，…，m-1）个位置；基数a（m+1+k，n-k+1）（k=1，2，…，m）所在行的元素向右顺移r（n-k·m）（k=0，1，2，…，m-1）个位置.

设方阵B位于第i行、第j列元素为b（i，j），方阵A第m+1-k行的元素向右顺移r（k·m）（k=0，1，2，…，m-1）个位置，所以

当各行都完成了这一程序之后，所得方阵B就是一个对称幻方（当n是3的倍数时）或是一个对称完美幻方（当n不是3的倍数时）.接着，对上述对称幻方或对称完美幻方作行变换，即对方阵B作行变换得n阶方阵C.

对方阵B作行变换，方阵B的第r（m-2i）行作为方阵C的第i+1行（i=0，1，…，m-1）；m+1行仍作为第m+1 行；笫r（m-1-2i）行作为第m+2+i（i=0，1，…，m-1）行.得方阵C就是奇偶分开的对称幻方（定理2）.

上述方法我们称之为构造奇偶分开的对称幻方的匹配余函数两步法.

注意，若不是用以上的行变换方法，而用其他的行变换，虽可使奇数集中于方阵中央的菱形中，而偶数则置于方阵的四角，但变换的结果并不是幻方.这是由于对角线上数字之和不等于幻方常数，故所得的是方阵.

定理2 用匹配余函数两步法得到的n=2m+1（m=1，2，…）阶方阵C是一个奇偶分开的对称幻方.

证明 1）由安装基方阵A时要求：匹配基数必须置于对称列中，笫一列取奇基数，然后从左到右奇基数与偶基数相间隔，取定d1=1，dm+1=m+1，dn=n，且k为奇数时dk为奇数，k为偶数时dk为偶数，奇偶数相间隔.基方阵A中，显然，奇基数所在行中它的右侧所有元素都是奇数而左侧所有元素都是偶数，偶基数所在行中它的右侧所有元素都是偶数而左侧所有元素都是奇数.

第r（m-2i）行（i=0，1，…，m-1）上的基数位于笫r（2i+2）列是偶基数其左侧所有元素都是奇数，共有2i+1个奇数，中间那个奇数位于第i+1列，即a（m-2i，i+1）是中间那个奇数.

第m+1 行全部是奇数.笫r（m-1-2i）（i=0，1，…，m-1）行上的基数位于笫r（2i+2）列是奇基数其右侧所有元素都是奇数，有n-（2i+2）=2m-2i-1个奇数，中间那个奇数位于第m+i+2列.即r（m-1-2i，m+i+2）是中间那个奇数.

2）下面证明方阵B就是一个对称幻方.

当i为1～n-2的奇数时，r（mi）是m～1由大至小的自然数；当i为2～n-1的偶数时，r（mi）是n-1～m+1由大至小的自然数；当i=n时，r（mi）=n.即i取遍1～n的自然数时，r（mi）亦取遍1～n的自然数.

当i为1～n的奇数时，是m+1～n的自然数；当i为2～n-1的偶数时，r（（m+1）i）是1～m的自然数；当i=n时，r（（m+1）i）=n.即i取遍1～n的自然数时，r（（m+1）i）亦取遍1～n的自然数.

方阵B位于第i行、第j列的元素为

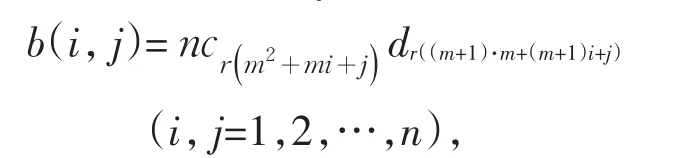
注意到在求和过程中m2+j与（m+1）·m+j是常数，以及余函数的定义和上述关于r（mi），r（（m+1）i）的讨论，方阵B第j列（j=1，2，…，n）元素之和为

即等于n阶幻方的幻方常数.

由于方阵B第i行（i=1，2，…，n）与方阵A第i行的元素相同，所以方阵B第i行（i=1，2，…，n）元素之和亦等于n阶幻方的幻方常数.

基方阵A是中心对称的，而方阵B是由基方阵A施行顺移所得，由于方阵A第m+1-k行的元素向右顺移r（k·m）（k=0，1，2，…，m-1）个位置，方阵A第m+1+k（k=1，2，…，m）行的元素向右顺移r（n-k·m）（k=1，2，…，m）个位置，即向左顺移r（k·m）（k=1，2，…，m）个位置，而笫m+1行的元素不动.所以方阵B仍是中心对称的，故方阵B两对角线上元素之和都等于n阶幻方的幻方常数.所以方阵B是对称幻方.

3）接着要证明方阵B各行的奇数都集中于该行的正中，而偶数平均地置于两侧.

基方阵A第r（m-2i）行（i=0，1，…，m-1）上，共有2i+1个奇数，而中间那个奇数位于第i+1列，即a（m-2i，i+1）是中间那个奇数.若要b（m-2i，m+1）=a（m-2i，i+1），则该行的元素必须向右顺移（m+1）-（i+1）=m-i个位置.顺移的结果就是b（m-2i，m+1）=a（m-2i，i+1）.

基方阵A笫r（m-1-2i）（i=0，1，…，m-1）行上，共有n-（2i+2）=2m-2i-1个奇数，中间那个奇数位于第m+i+2列.即a（m-1-2i，m+2+i）是中间那个奇数.若要

b（m-1-2i，m+1）=a（m-1-2i，m+2+i），

则该行的元素必须向右顺移（n+m+1）-（m+2+i）=2m-i个位置.顺移的结果就是

b（m-1-2i，m+1）=a（m-1-2i，m+2+i）.（a）对n=2（2s）+1=4s+1（s=1，2，…），当i=0，1，…，s-1时，基方阵A第r（m-2i）行即第r（m+1-（2i+1））行的元素若向右顺移r（（2i+1）m）（i=0，1，…，s-1），即r（（2i+1）m）=r（（2m+1）i+（m-i））=m-i个位置.顺移的结果是

b（m-2i，m+1）=a（m-2i，i+1）.当i=s，s+1，…，2s-1时，基方阵A第r（m-2i）行即位于基方阵A下半部分的第n+m-2i行，r（m-2i）=r（m+1+（-（2i+1）））若第r（m-2i）行向右顺移r（n-（-（2i+1））m）（i=s，s+1，…，2s-1），即r（n-（-（2i+1））m）=r（n+（2i+1）m）=r（（2i+1）m）=m-i个位置.顺移的结果是

b（m-2i，m+1）=a（m-2i，i+1）.当i=0，1，…，s-1时，基方阵A第r（m-1-2i）行即第r（m+1-（2i+2））的元素若向右顺移r（（2i+2）×m）（i=0，1，…，s-1），即r（（2i+2）m）=r（（2m+1）i+（2m-i））=2m-i个位置.顺移的结果是

b（m-1-2i，m+1）=a（m-1-2i，m+2+i）.当i=s，s+1，…，2s-1时，基方阵A第r（m-1-2i）行即位于基方阵A下半部分的第n+m-1-2i行，r（m-1-2i）=r（m+1+（-（2i+2）））若第r（m-1-2i）行向右顺移r（n-（-（2i+2））m）（i=s，s+1，…，2s-1），即r（n-（-（2i+2））m）=r（n+（2i+2）m）=r（（2i+2）m）=2m-i个位置.顺移的结果是

b（m-1-2i，m+1）=a（m-1-2i，m+2+i）.（b）对n=2（2s+1）+1=4s+3（s=1，2，…），当i=0，1，…，s时，基方阵A第r（m-2i）行即第r（m+1-（2i+1））若向右顺移r（（2i+1）m）（i=0，1，…，s），即

r（（2i+1）m）=r（（2m+1）i+（m-i））=m-i个位置.顺移的结果是

b（m-2i，m+1）=a（m-2i，i+1）.当i=s+1，s+2，…，2s时，基方阵A第r（m-2i）行即位于基方阵A下半部分的第n+m-2i行，r（m-2i）=r（m+1+（-（2i+1）））第r（m-2i）行向右顺移r（n-（-（2i+1））m）（i=s+1，s+2，…，2s），即r（n-（-（2i+1））·m）=r（n+（2i+1）m）=r（（2i+1）m）=m-i个位置.顺移的结果是

b（m-2i，m+1）=a（m-2i，i+1）.当i=0，1，…，s时，基方阵A第r（m-1-2i）行即第r（m+1+（-（2i+2））若向右顺移r（（2i+2）m）（i=0，1，…，s），即r（（2i+2）m）=r（（2m+1）i+（2m-i））=2m-i个位置.顺移的结果是

b（m-1-2i，m+1）=a（m-1-2i，m+2+i）.当i=s+1，s+2，…，2s时，基方阵A第r（m-1-2i）行即位于基方阵A下半部分的第n+m-1-2i行，

r（m-1-2i）=r（m+1+（-（2i+2）））若第r（m-1-2i）行向右顺移r（n-（-（2i+2））m）（i=s，s+1，…，2s-1），即r（n-（-（2i+2））m）=r（n+（2i+2）m）=r（（2i+2）m）=2m-i个位置.

综上所述对n=2m+1（m=1，2，…），方阵B不仅是一个对称幻方且其各行的奇数都集中于该行的正中，而偶数平均地置于两侧.

4）证明方阵C是一个奇偶分开的对称幻方.

对方阵B所作行变换是把方阵B的第r（m-2i）行作为方阵C的第i+1（i=0，1，…，m-1）行；第m+1行仍作为第m+1行；笫r（m-1-2i）行作为第m+2+i（i=0，1，…，m-1）行.

与方阵C的第i+1（i=0，1，…，m-1）行的处于对称位置的是方阵C第n-i行，由于我们讨论的是奇数阶幻方，所以i+1与n-i的奇偶性相同.

方阵C的第i+1（i=0，1，…，m-1）行即方阵B的第r（m-2i）行，而方阵C的第n-i=（n-i-1）+1行即方阵B的第r（m-2（n-i-1））=r（m+2+2i）行，方阵B中的这两行的元素是中心对称，所以方阵C的第i+1行与方阵C的第n-i行的元素是中心对称.

与方阵C的第m+2+i（i=0，1，…，m-1）行处于对称位置的是方阵C第m-i行，由于我们讨论的是奇数阶幻方，所以m+2+i与m-i的奇偶性相同.

方阵C的第m+2+i（i=0，1，…，m-1）行即方阵B的第r（m-1-2i）行，而方阵C的第m-i=m+2-（i+2）行即方阵B的第r（m-1-2（-（i+2）））=r（m+3+2i）行，方阵B中的这两行的元素是中心对称，所以方阵C的第m+2+i行与方阵C的第m-i行的元素是中心对称.

可见方阵C是中心对称的，因而方阵C两对角线上元素之和都等于n阶幻方的幻方常数.又因方阵C是方阵B作行变换所得，故方阵C仍是对称幻方.且其各行的奇数都集中于该行的正中，而偶数平均地置于两侧.又已知方阵C第i+1（i=0，1，…，m-1）行有2i+1个奇数，第m+2+i（i=0，1，…，m-1）行有2m-（2i+1）个奇数，第m+1行有2m+1个奇数，所以方阵C是一个奇偶分开的对称幻方.定理证毕.

笫二步所得的每一个对称幻方或对称完美幻方通过上述的行变换可得到一个奇偶分开的对称幻方，所以，当n=2m+1（m=2k，k=1，2，…）时，用匹配余函数两步法构造出2m(k!)2·2m-1(k !)(( k-1)!)个不同的n阶奇偶分开的对称幻方；当n=2m+1（m=2k+1，k=1，2，…）时，可构造出

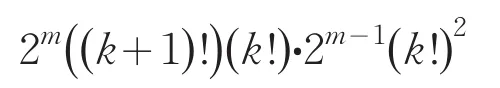
个不同的n阶奇偶分开的对称幻方.

[1]王辉丰,詹森.关于构造三类奇数阶幻方的新方法[J].海南师范大学学报:自然科学版,2010,23(1):12-15.

[2]詹森,王辉丰.奇数阶对称完美幻方的构造方法[J].海南师范大学学报:自然科学版,2009,22(4):396-402.

[3]詹森,王辉丰.构造奇数阶幻方,完美幻方和对称完美幻方的新方法[J].海南师范大学学报:自然科学版,2011,24(3):265-269.

The New Structure Methods about Odd Order Symmetrical Magic Square and Symmetrical Magic Square with Separated Odd and Even Numbers

ZHAN Sen1，WANG Huifeng2

（1.Department of Computer Science，Guangdong Technical Normal University，Guangzhou510665，China；2.College of Mathematics and Statistics，Hainan Normal University，Haikou571158，China）

The new structure method called two-step matching method were given and proved,which could obtain oddnorder symmetrical magic square.The new structure method called two-step matching residual function method were given and proved,which could obtain symmetrical magic square with separated odd and even numbers.These methods may obtain2m(m!)·2m-1(( m-1)!)differentnorder symmetrical magic squares;whenn=2m+1（m=2k，k=1，2，…）may obtain2m(k!)2·2m-1(k!)((k-1)!)differentnorder symmetrical magic square with separated odd and even numbers;whenn=2m+1（m=2k+1，k=0，1，2，…）may obtain2m(( k+1)!)(k!)·2m-1(k !)2differentnorder symmetrical magic square with separated odd and even numbers.

symmetrical magic square；symmetrical magic square with separated odd and even numbers；matching car⁃dinal number；residual function

O 157.6

A

1674-4942（2011）04-0395-05

2011-10-15

黄 澜