有限集合上封闭集族的计数（续）

唐保祥，任 韩

（1.天水师范学院 数学与统计学院，甘肃 天水 741001；2.华东师范大学 数学系，上海 200062）

有限集合上封闭集族的计数（续）

唐保祥1，任 韩2

（1.天水师范学院 数学与统计学院，甘肃 天水 741001；2.华东师范大学 数学系，上海 200062）

子集；幂集；封闭集族

1 前言

计数问题是组合数学研究的重要课题之一，具有广泛的应用背景和重要的理论意义.然而，大量的计数问题没有系统方法和工具来统一解决.通常人们面对具体问题，创造出了许多精巧的计数方法来解决问题[1-14]，从而丰富和推动了组合数学的发展.

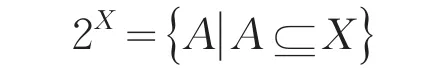
2 结果及证明

设集合X={a1,a2,a3,…,an},本文用f（n，m）并表示X上有m个元素的所有不同的封闭集族的数目.对任意正整数n，为了得到m=2，3，4，5时（fn，m）的值，首先给出：

引理1[14]设Z+为正整数集合，∀m,n,i,j,k,l∈Z+，则下面结论成立：

[1]栾汝书.分类集及极大分类集的计数[J].清华大学学报:自然科学版,1989,29(3):1-6.

[2]王元元,王庆瑞,黄纪麟,等.组合数学理论与题解[M].上海:上海科学技术文献出版社,1989.

[3]耿素云,曲婉玲.离散数学(修订版)[M].北京:高等教育出版社,2004.

[4]田秋成.组合数学[M].北京:电子工业出版社,2006.

[5]康庆德.组合学笔记[M].北京:科学出版社,2009.

[6]王天明.近代组合学[M].大连:大连理工大学出版社,2008.

[7]Richard P Stanley.计数组合学(第一卷)[M].付梅,侯庆虎,辛国策,等译.北京:高等教育出版社,2009.

[8]李磊.关于几个组合计数公式的推广[J].工程数学学报,1996,13(4):95-98.

[9]陈宁宇,张武.不相邻重排列的一种计数方法[J].上海大学学报:自然科学版,2005,11(1):60-62.

[10]Sprugnoli R.Riordan arrays and the Abel-Gould identity[J].Discrete Mathematics,1995,142(1-3):213-233.

[11]Krattenthaler C,Mohants S G.Counting tableaux with row and column bounds[J].Discrete Mathematics,1995,139:237-285.

[12]Hsu L C,Peier Jau Shyong Shiue.On a combinatorial ex⁃pression concerning Fermat’s Last Theorem[J].Advanc⁃es in Applied Mathematics,1997,18:216-219.

[13]He T X,Hsu L C,Shiue P J S,et al.Asymbolic operator approach to several summation formulas for power series[J].Journal of Computational and Applied Mathematics,2005,177(1):17-33.

[14]唐保祥,任韩.有限集合上封闭集族的计数[J].中山大学学报:自然科学版,2010,49(6):11-14.

Enumeration of Closed Family of Finite Sets(Continued)

TANG Baoxiang1，REN Han2
（1.School of Mathematics and Statistics，Tianshui Normal University，Tianshui741001，China；2.Department of Mathematics，East China Normal University，Shanghai200062，China）

subset；power set；closed family of sets

O 157.1

A

1674-4942（2011）04-0391-04

2011-09-18

国家自然科学基金资助项目（11171114）

毕和平