一种改进的降低OFDM峰均比的压扩算法

王兰勋，丁全，杨康

（河北大学 电子信息工程学院，河北 保定 071002）

一种改进的降低OFDM峰均比的压扩算法

王兰勋，丁全，杨康

（河北大学 电子信息工程学院，河北 保定 071002）

通过对正交频分复用（orthogonal frequency division multiplexing—OFDM）峰均比的研究，提出一种改进压扩C变换的方法来降低OFDM系统中的峰均比（PAPR）.该算法是在原有的压扩C变换方法基础上，通过适当修改某些参数，来达到进一步降低PAPR的目的.仿真结果表明该改进算法更有效地抑制了PAPR的同时，系统的误码率略有增加，而算法复杂度与传统算法相比并没有提升.该改进算法是误码率与峰均比性能的折中，具有实用性.

正交频分复用；压扩C变换；峰均比

移动通信是现代通信系统中不可缺少的组成部分，随着第3代移动通信技术的日渐完善和普及，以OFDM（orthogonal frequency division multiplexing）为关键技术之一的第4代移动通信系统的研究逐渐吸引着人们的目光.OFDM（orthogonal frequency division multiplexing）［1］，即正交频分复用具有良好的频谱利用率和抗信道衰落能力，但是由于OFDM符号是由多个独立的经过调制的子载波信号相加而成，因此在某个时刻，若多个子载波向同一个方向相加时，就会产生较大的峰值功率.这些大的峰值功率会影响系统中功率放大器和模数、数模转换器的正常工作状态，从而影响到系统的误码率，因此研究OFDM系统的峰值功率以及怎样减少峰值功率和平均功率的比值即峰均功率比（PAPR），就有重要的意义.

目前，抑制PAPR的方法主要可以归为3类：预畸变类、编码类和非畸变类［2］.第1类预畸变技术，这类技术的主要特点是对非线性的高峰值信号幅度直接进行处理，具有不可逆性，系统实现简单，但是这类技术带来带外辐射和带内噪声使系统性能恶化.第2类编码类技术，其基本原理是利用各种类型的编码来避免出现峰均功率比较大的OFDM符号，但此技术编解码的计算复杂度非常高.第3类非畸变技术通过对信号进行线性变换，来降低高PAPR出现的概率，但通常需要很高的计算复杂度和硬件实现.

笔者针对第1类预畸变技术中的压扩C变换算法进行了讨论，在介绍了传统的压扩C变换算法的基础上，提出具有更好PAPR性能的改进算法.

1 OFDM系统中的PAPR

1个OFDM信号由多个子载波信号构成，当在某3个时刻，存在多个子载波向同一个方向相加时，就会出现较大的峰均功率（peak-to-average power，PAP）.例如存在N个子载波的OFDM系统，若某一时刻，N个子载波都向同一相位相加，那么峰值功率就是平均功率的N倍［3-9］.

峰值功率与平均功率比，一般定义如下：

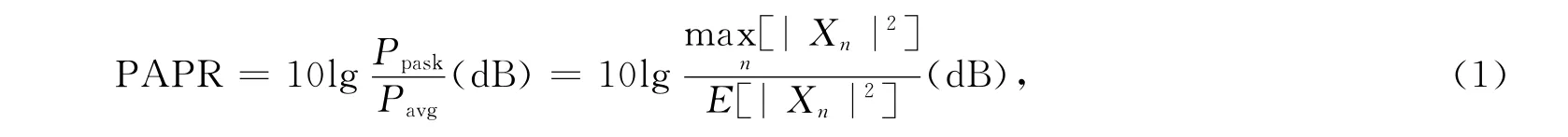
上式中，Xn表示已调的OFDM信号，E［·］表示数学期望即平均值.为了示OFDM系统中PAPR的统计特性，常引入PAPR的互补累计分布函数（complementary cumulative distribution function——CCDF）的概念.互补累计分布函数定义为多载波系统中峰均比值超过某一门限值z的概率

2 原始压扩算法

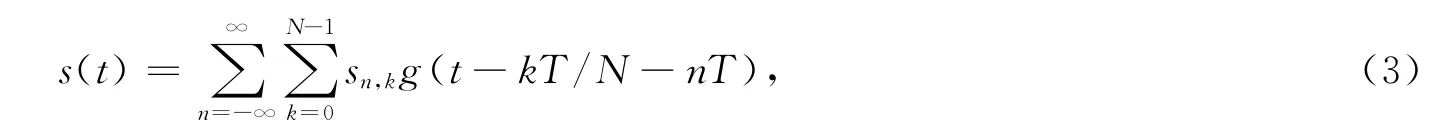
式中，T表示OFDM信号的长度，k表示一个符号周期内第k个采样值，n表示时域内的第n个OFDM信号，g（t）表示满足奈奎斯特脉冲滤波器的冲激响应，sn，k表示经过变换的第n个OFDM信号中的第k个采样值，即sn，k＝C｛sn，k｝，其中，xn，k表示经过调制的 OFDM 信号，C｛·｝表示压扩变换：当｜x｜≤m时，｜C｛X｝｜≥｜x｜；否则｜C｛X｝｜≤｜x｜，m代表C变换的点；并要满足E｛｜X｜2｝≈E｛C｛｜X｝｜2｝，也就是说变换前后的功率要大致相等.

如果适当选择C变换的形式和转折点m，那么就可以显著改善PAPR性能，并且没有使系统变得更加复杂，C变换可以用下式来描述：

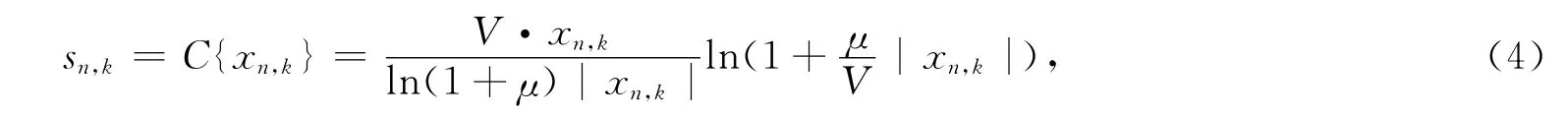
传统压扩变换的基本思想就是把大功率发射信号压缩，而把小功率发射信号放大，从而能够使信号的平均功率保持不变，这样既可以提高系统的抗干扰能力，也能够减小PAPR［10］.

在OFDM系统中，输出信号的复基带信号可以表示为

式中V代表OFDM信号xn，k的平均幅值，也就是C变换的转折点，μ通常情况下不大于5.变换后的峰值信号为

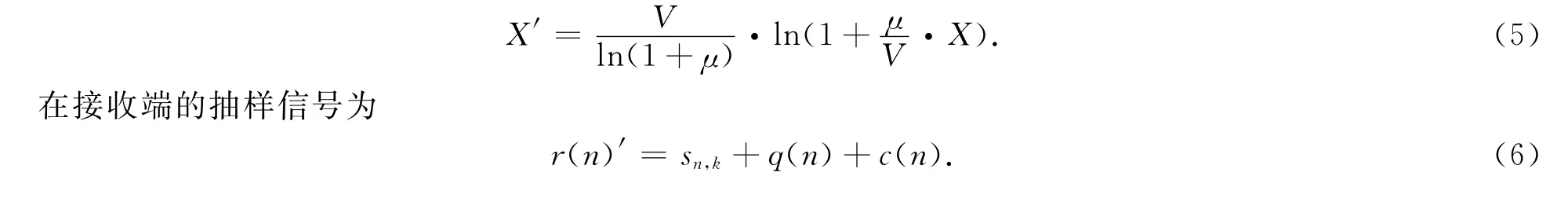
上式中，xn，k是 OFDM 信号，q（n）是D／A转换器的量化噪声，c（n）是信道噪声.对式（6）进行C逆变换，即

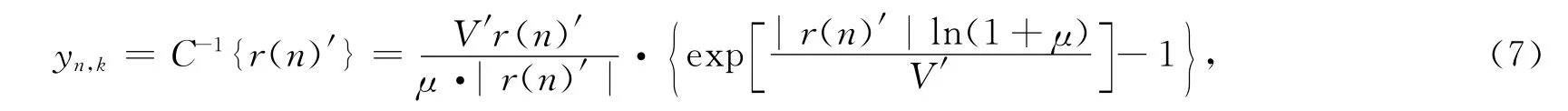
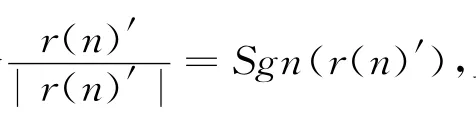
由上式可以得出经过C变换后，大幅值信号减少，且这种算法较概率类算法来说，简单，易实现，不存在迭代的过程.但是，这个过程是非线性的过程，因此需要考虑误码率等的因素.图1为OFDM原始信号时域图，图2为经过压扩算法的OFDM信号时域图从两图的对比，可以直观地看到压扩算法对OFDM信号的PAPR性能是有很大提高的.

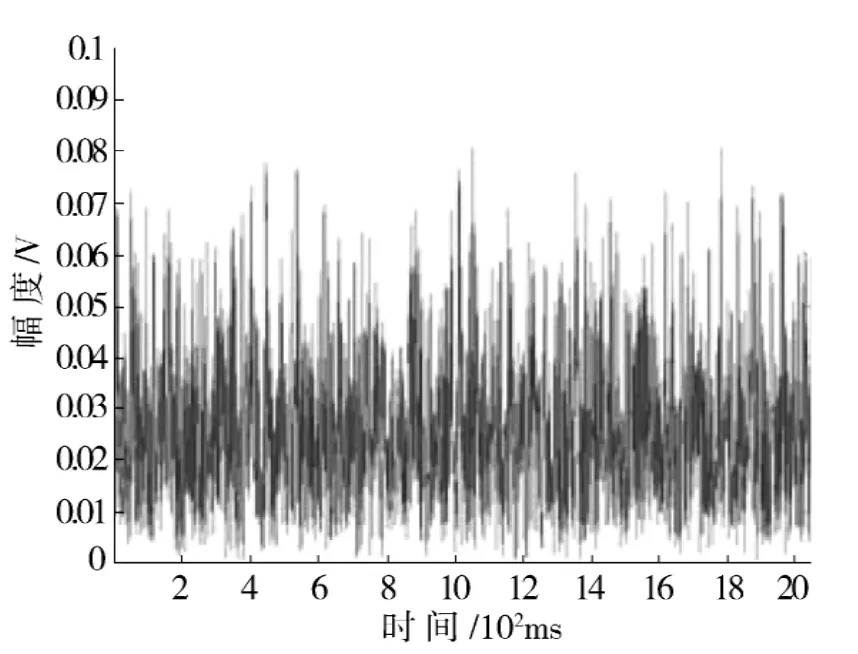
图1 OFDM原始信号Fig.1 OFDM original signal

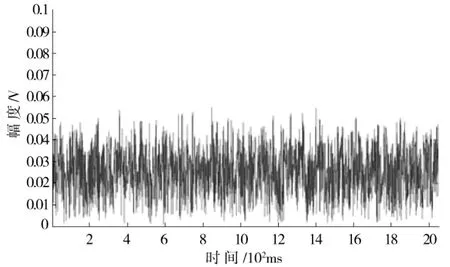
图2 经过压扩算法的OFDM信号Fig.2 Through the compression and expansion algorithm for OFDM signals

图3是原始压扩C变换的算法仿真图.

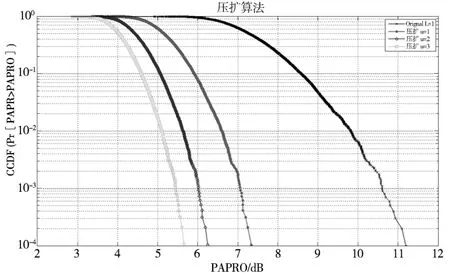
图3 原始压扩算法的PAPR仿真Fig.3 Original PAPR simulation of compression and expansion algorithm

表1给出了图3的数据分析.可以看到，原始算法可以有效地改善系统的PAPR性能，并且随着μ的增大，对系统的PAPR的性能的改善也越大.在系统PAPR概率为10-3时，对于不同的μ值，分别有1.703dB，和0.554dB的改善.在实际中，因为随着μ的增大，压扩算法对系统PAPR的性能会降低，因此通常μ≤5.

表1 CCDF在10-3处，不同μ值所对应的PAPR值Tab.1 CCDF in 10-3，PAPR values corresponding to different values ofμ

3 改进的压扩算法

在传统的压扩变换过程中，一般采取对小信号幅值扩大，对大信号幅值减小的放大来达到降低PAPR的目的，但是随着μ的增大会引起限幅噪声以及误码率的增多，使系统性能下降.因此，笔者提出一种改进的压扩变换算法，利用改进的压扩算法，可以在不增大太多误码率的条件下，使OFDM系统的PAPR性能得到较大的改善和提高.在改进的算法中，对式（4）中的V，由原来的信号幅值的平均值，改为信号功率的平均值，如式（11）所示.

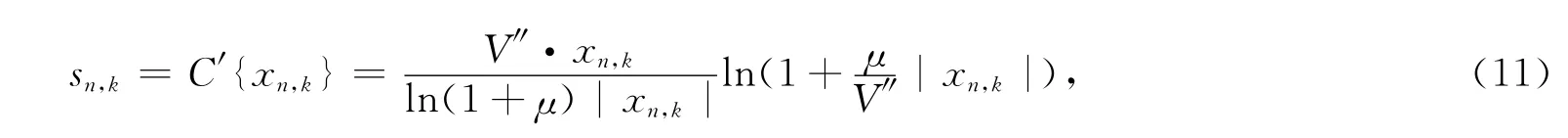
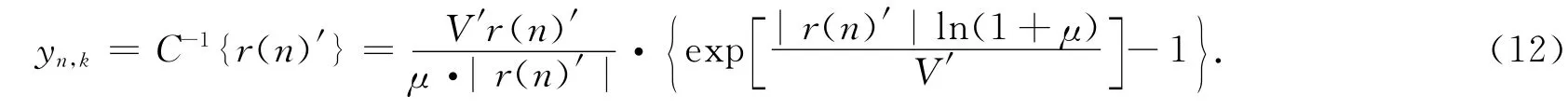
在接收端的C反变换中，V′代表的是接收信号的平均幅度.

下面对改进算法进行Matlab仿真实验.其CCDF仿真结果如图4所示，仿真参数为，N＝256，采用QPSK调制，4倍过采样.

式中，V″代表信号的平均功率，也就是C变换的转折点.这样，可以大幅度提高C变换的转折点，也就是说，这样可以使得被畸变的信号大幅度减少，但是会牺牲一些信号的功率，同时使得PAPR的性能可以大幅度的提高.在接收端，如式（7）所示，对信号进行C反变换，这里写为式（12）.

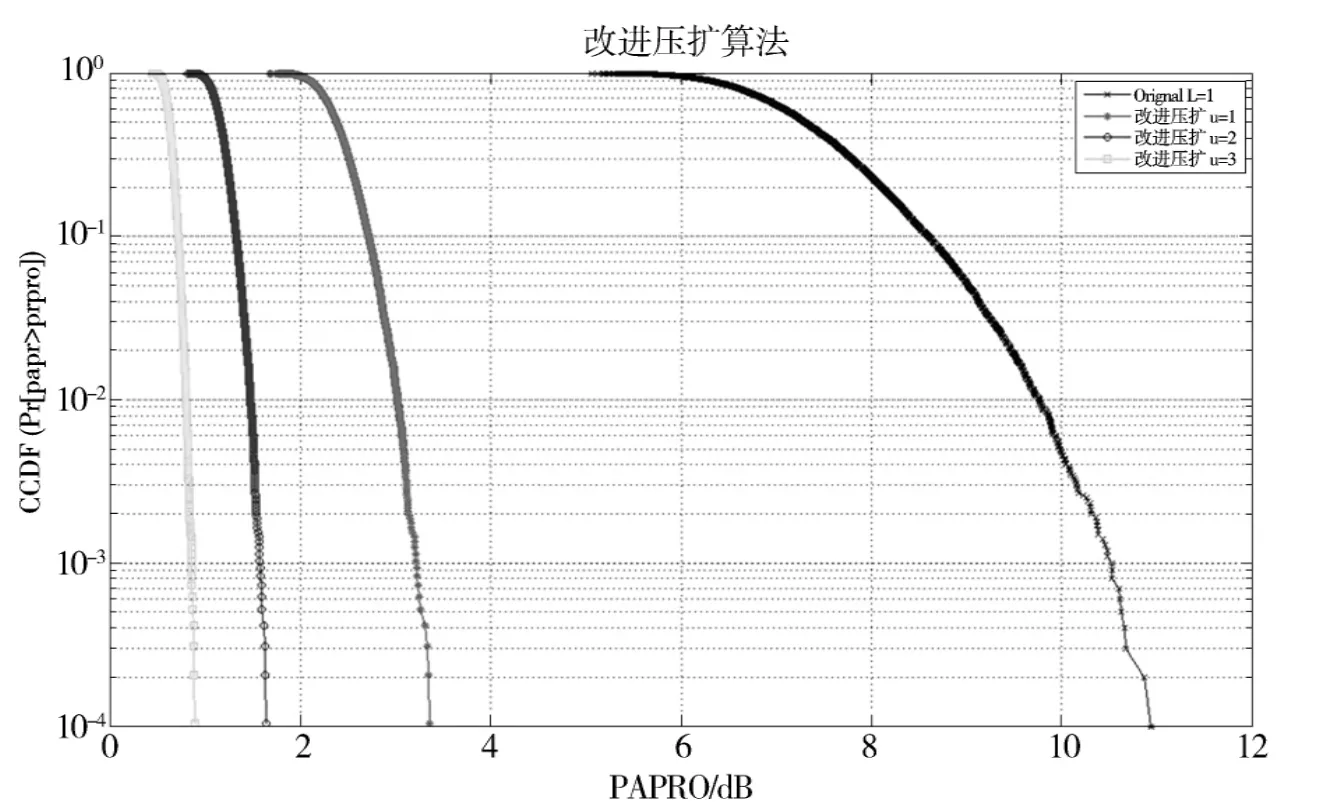
图4 改进压扩算法的PAPR仿真Fig.4 Improved PAPR simulation of compression and expansion algorithm

图4中自左向右依次为μ＝1，μ＝2，μ＝3的改进算法的CCDF曲线.表2给出了改进算在10-3处，不同μ所对应的PAPR值.

表2 CCDF在10-3处，不同μ值所对应的PAPR值Tab.2 CCDF in 10-3，PAPR values corresponding to different values ofμ

通过2组数据对比，在10-3处，可以得到改进算法在μ＝1时，相对于原始算法提高了4.461dB；在μ＝2时，相对于原始算法，提高了4.415dB；在μ＝3时，相对于原始算法提高了4.588dB.

显然改进算法也属于预畸变类的算法，其对系统误码率的影响如图5所示.从图5可以看出，改进算法把误码率控制在一定范围的情况下，使系统PAPR性能大幅提高.

图5 原始算法与改进算法的误码率对比Fig.5 Original algorithm and improved calculation of the error rate comparison chart

4 总结

本文基于传统压扩传统算法的基本原理，提出了改进的压扩算法，改进的压扩算法在略微增加系统误码率的条件下，使得系统的PAPR性能大幅度提高，该算法具有较大的实用性，是误码率与PAPR性能的较完美的折中，具有一定的经济价值.

［1］佟学俭，罗涛.OFDM移动通信技术原理与应用［M］.北京：人民邮电出版社，2003.

［2］汪裕民.OFDM关键技术应用［M］.北京：机械工业出版社，2007.

［3］YANG L，CHEN R S，SIU Y M，et al.PAPR reduction of an OFDM signal by use of PTS with low computational complexity［J］.IEEE Trans Broadcast，2006，52（1）：83-86.

［4］LIM D W，SEON J，LIM C W，et al.A new SLM OFDM scheme with low complexity for PAPR reduction［J］.IEEE Signal Processing Letters，2005，12（2）：93-96.

［5］ARMSTRONG J.Peak-to-average power reduction for OFDM by repeated clipping and frequency Domain diltering［J］.E-lectronics Letters，2002，38（5）：246-247.

［6］HAN S H，LEE J H.Reduetion of PAPR of an OFDM signal by partial transmit sequence technique with reduced complexity［J］.IEEE Globeeom，2003（8）：1326一1329

［7］WANG C L，OUYANG Y.Low complexity selected map-ping schemes for peak-to-average power ratio reduction in OFDM systems［J］.IEEE Transactions on Signal Processing，2005，53（12）：4652-4660.

［8］HAN S H，LEE J H.PAPR reduction of OFDM signals using a reduced complexity PTS technique［J］.IEEE Signal Processing Letters，2004，11（11）：887-890.

［9］DAE-WOON LIM，HONG-SEON NO，CHI-WOO-LIM，et al.A new SLM OFDM scheme with low complexity for PAPR reduction［J］.IEEE Signal Processing Letters，2005，12（2）：93-96.

［10］尹长川，罗涛，乐光新.多载波宽带无线通信技术［M］.北京：北京邮电大学出版社，2004：105-107.

An Improved Algorithm of the Companding to Reduce the PAPR for OFDM System

WANG Lan-xun，DING Quan，YANG Kang
（College of Electronic and Information al Engineering，Hebei University，Baoding 071002，China）

On orthogonal frequency division multiplexing（OFDM）of PAPR，an improved compression and expansion C transformation method was applied to reduce peak-to-average power ratio （PAPR）in OFDM systems.The improved algorithm was the compression and expansion in the original C transformation method，based on certain parameters through appropriate changes to achieve the objective of further reducing PAPR.Simulation results showed that the improved algorithm was more effective in inhibiting the PAPR，the system's error rate increased slightly，while the algorithm complexity compared with the traditional method did not improve.The improved algorithm had bit error rate performance and PAPR performance of compromise，with practicality.

orthogonal frequency division multiplexing（OFDM）；ttraditional algorithm of compression and expansion C transformation；peak-to-average power ratio（PAPR）

TN 914

A

1000-1565（2011）05-0532-06

2010-08-30

河北大学科技攻关项目（06213552）

王兰勋（1956-），男，河北安平人，河北大学副教授，主要从事数字通信与信息编码方面研究.

E-mail：wanglanxun＠yahoo.com

孟素兰）