半线性抛物方程的门槛结果
戴求亿,顾永耕,刘 芳,谢君辉
(湖南师范大学数学与计算机科学学院,中国长沙 410081)
半线性抛物方程的门槛结果
戴求亿*,顾永耕,刘 芳,谢君辉
(湖南师范大学数学与计算机科学学院,中国长沙 410081)
研究了半线性抛物方程的初边值问题.证明了它对应的稳态问题的任意正解是该抛物问题整体解存在与否的初值门槛(结论的精确表述见本文定理1).
初边值问题;半线性抛物方程;稳态问题;门槛结果
1 Introduction
LetΩbe a bounded domain in Rn,and∂Ωdenote the boundary ofΩ,n≥2.Assume that(aij (x))n×nis a symmetric matrix withaij (x)∈Cα()fori,j=1,2,…,n,and that there exist positive numbersγandΓ such that for anyξ∈Rn,

Assume further thatc(x)∈Cα(ˉΩ),andu0(x)∈C(ˉΩ).The topic of this paper is the following initial-boundary value problem of parabolic equations
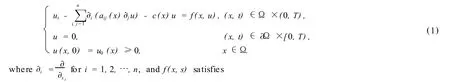
(F1)f(x,s)is locallyLipschitz and satisfies that there is constantsC>0 and 0<σ<1 such thatf(x, s)≥Cs1+σfors>0.
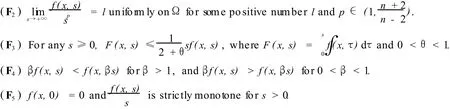
A typical example off(x,s)which satisfies(F1)~(F5)isf(x,s)bi≥0,andbi0≠0 for somei0∈{1,2,…,m}.
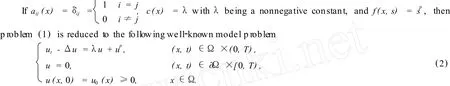
There are many literatures on problem(2).A priori bound for global solution of(2)can be found in[1], decaying rate estimate for global solution and blow-up rate estimate for blow-up solution of(2)were given in [2~3].There is also a well-known result on(2)which says that it has global solution when the initial datau0(x)is small enough in suitable sense and has no global solution whenu0(x)large enough in some sense[4]. However,the classification of initial datau0(x)according to the existence and nonexistence of global solution to(2)is not complete.Hence,a fundamental problem is to find exact conditions on the initial datau0(x)which can ensure the existence or nonexistence of global solution to(2).On this direction,there are some so called threshold results.To our knowledge,threshold results can be described by the energy of the initial datau0(x)[5-6],aswell as by solutions of the following steady-state problem[7-8]

Concerning the threshold result given by the energy of the initial data,Liu and Zhao[5]proved that the energy of the least energy solution of problem(3)is a threshold energy for the energy of initial datau0(x)to ensure the existence and nonexistence of global solution to problem(2).However,there is a few result on the higher energy case[9].Concerning the threshold result described by solutions of problem(3),Lacey[7]proved the following result.
Theorem AAssume thatU(x)is an arbitrary solution of problem(3).Then the following conclusions hold
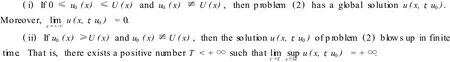
The main purpose of this paper is to generalize Theorem A to problem(1).That is,we focus on the threshold result of problem(1)described by solutions of the following steady-state problem

Ourmain result can be stated as
Theorem 1Assume thataij (x)satisfies(A)and thatf(x,s)satisfies(F1)~(F5).Assume further thatU(x)is an arbitrary solution of problem(4).Then the following conclusions hold

Remark 1If(A)and(F1)hold,then it follows from the semigroup theory and fixed point theorem that there exists a constantT>0 such that problem(1)has a classical solutionu(x,t;u0)inΩ×(0,T). Moreover,ifwe denote byTmaxthe maximal existence time ofu(x,t;u0),
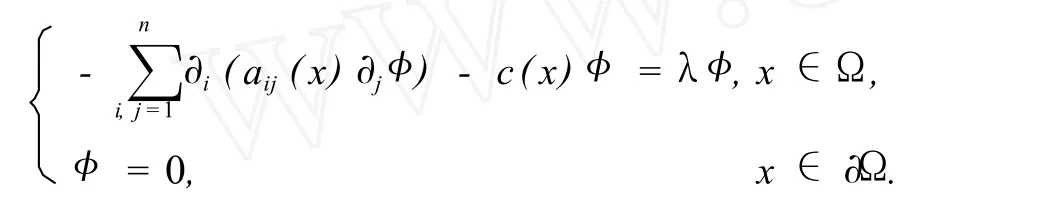
Remark 3Theorem A was proved by convexity method.However,this method has its drawback in applications,for example,it does not work for parabolic systems.Here,we present a new method to prove Theorem 1.This new method is applicable for any problem with the following properties
(i)Any two distinct positive steady-state solutions intersect each other.
(ii)Any global solution is uniformly bounded with respect to timet.
Remark 4Ourmethod can be applied to the parabolic systems and a similar result to that of Theorem 1 can be proved.
The rest of this paper is arranged as follows:Section 2 devotes to derive a priori estimate for the global solution of problem(1).The proof of Theorem 1 is included in section 3.
2 A Priori Bound for the Global Solution of Problem(1)
In this section,we derive a priori bound for global solution of problem(1).More precisely,wewillprove the following theorem.
Theorem 2Assume that(A)and(F1)~(F5)hold.Ifu(x,t)is a classical solution of problem(1) inΩ×(0,+∞)with 0≤u0(x)∈C(Ω),then there exists a positive constantMindependent oftsuch thatu(x,t)≤Mfor any(x,t)∈Ω×(0,+∞).
The proof of this theorem can adopt from[1]line by line with some minor modifications.For convenience,we give a sketch proof here.This proof is divided into the following series lemmas.
Lemma 1[11]Ifu(x)is a solution of problem
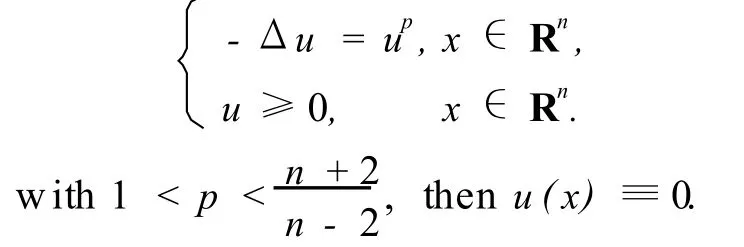
Remark 2Under the assumptions that(A)and(F1)~(F5)hold,by the same arguments used in [10]we can prove that problem(4)has at least one solution if and only if the first eigenvalueλ1(Ω)of the following eigenvalue problem is positive


Identity(10)says that the energyE(t)should decrease.This togetherwith(9)and(F4)shows thatE(t)≥0 for anyt>0.Otherwise,(9)and(F3)will imply that theL2norm of the solution must blow up in finite time.
Integrating(10)over(t′,T)gives
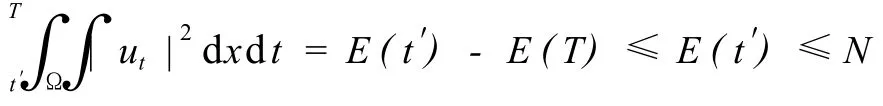
for some constantNindependent ofT.ApplyingLemma 3 withQ=Ω×[t′,T),we know that any solutioninΩ×[t′,T)which attains its maximum outsideΩ×[t′,2t′)is bounded from above by a constantMindependent ofT.By(8)we know that a solutionwhich take itsmaximum insideΩ×[t′,2t′)is dominated byB.Hence in any case

Combining(8)with(11),we reach the desired conclusion of Theorem 2.
3 The Proof of Theorem 1
We give a proof of Theorem 1 in this section.To this end,we need the following lemma first.
Lemma 4Ifu1(x)andu2(x)are any two distinct solutions of problem(4),thenu1(x)andu2(x)must intersect somewhere.
ProofSinceu1(x)andu2(x)are solutions of problem(4),we have
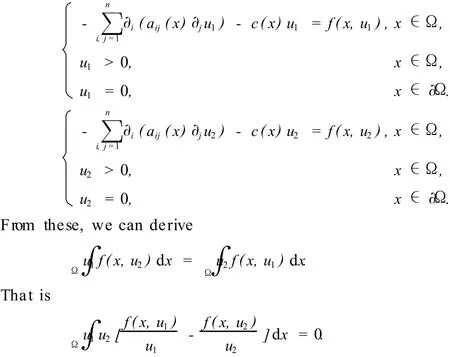
Combining this identity with(F5),we can easily see thatLemma 4 is true.
Proof of Theorem 1(i)If 0≤u0(x)≤U(x)andu0(x)≢U(x),then problem(1)has a global solutionu(x,t;u0).Moreover,by the strong comparison principle,we have

Then,it is easy to check that the following energy identities hold
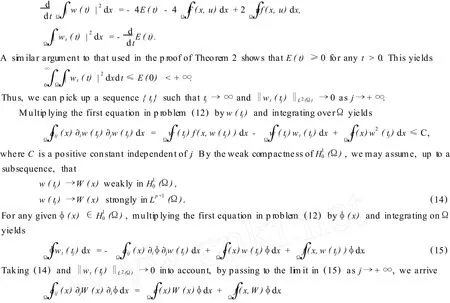
This implies thatW(x)is a weak solution of problem(13).By standard regularity theory of elliptic equations,W(x)is also a classical solution ofproblem(13).This togetherwith(F5)will imply thatW(x)≡0.Otherwise,on one hand,strongmaximum principle and(F1)should implyW(x)>0,on the other hand, strong comparison principle should implyW(x)<U(x)sincehβ(x)<U(x).This contradictsLemma 4 sinceW(x)andU(x)are two solutions of problem(4)which do not intersect each other.Thus,we have

This completes the proof of Theorem 1(i).
Finally,we prove Theorem 1(ii)by contradiction.To this end,we assume thatu0(x)≥U(x),u0(x)≢U(x),and problem(1)has a global solutionu(x,t;u0).By the strong comparison principle,we have

This implies thatHβ(x)is a strict sub-solution of the following problem
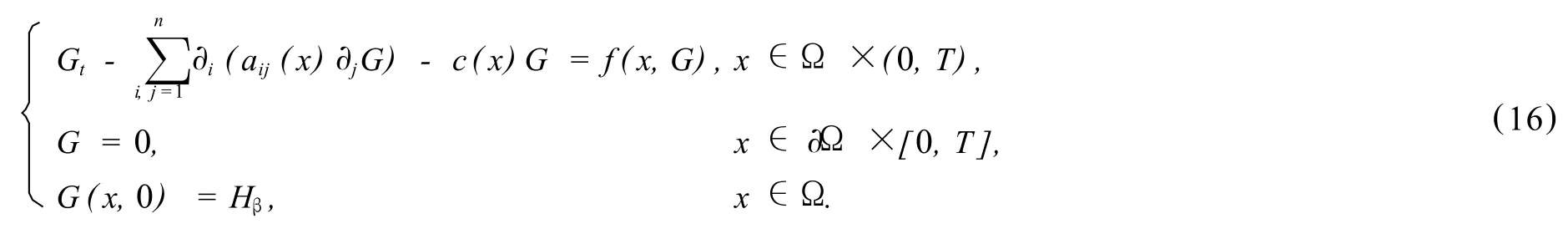
LetG(x,t)be the solution of problem(16).Then,it follows from the comparison principle thatG(x,t)≤u(x,t;u0)for any(x,t)due toHβ(x)≤u0(x).Consequently,G(x,t)exists globally and is strictly increasing int.By Theorem 2,there exists a positive constantMindependent oftsuch thatG(x,t)≤Mfor any(x,t).Hence,G(x,t)converges to some functiong(x).A similar argument to that used in the proof of Theorem 1(i)above shows thatg(x)is a solution ofproblem(4).Noting thatHβ(x)>U(x),it follows from the strong comparison principle thatG(x,t)>U(x)for any(x,t).Consequently,g(x)>U(x).This contradictsLemma 4 sinceg(x)andU(x)are two solutionsofproblem(4)which do not intersect each other.
[1] GIGA Y.A bound for global solutions of semilinear heat equations[J].Comm Math Phys,1986,103(3):415-421.
[2] POLACIK P,QU ITTNER P,SOUPLET P.Singularity and decay estimates in superlinear problems via Liouville-type theorems. PartⅡ:Parabolic equations[J].Indiana UnivMath J,2007,56(2):879-908.
[3] POLACIK P,QU ITTNER P,SOUPLET P.Singularity and decay estimates in superlinear problems via Liouville-type theorems. PartⅠ:Elliptic equations and systems[J].DukeMath J,2007,139(3):555-579.
[4] LEV INE H A.Some nonexistence and instability theorems for solutions of for mally parabolic equations of the formPut=-Au+F(u)[J].Arch RationalMech Anal,1973,51(5):371-386.
[5] L IU Y C,ZHAO J S.On potentialwells and applications to semilinear hyperbolic equations and parabolic equations[J].NonlinearAnal,2006,64(12):2665-2687.
[6] XU R Z.Asymptotic behavior and blow up of solutions for semilinearparabolic equations at critical energy level[J].Math Comput Simulation,2009,80(4):808-813.
[7] LACEYA A.Mathematical analysis of thermal runaway for spatially inhomogeneous reactions[J].Siam J ApplMath,1983,43 (6):1350-1366.
[8] MA L,SU N.Existence,multiplicity and stability results for positive solutions of nonlinearp-Laplacian equations[J].China AnnMath,2004,25B(2):275-286.
[9] GAZZOLA F,WETH T.Finite t ime blow-up and global solutions for semilinear parabolic equationswith initial data at high energy level[J].Diff Inte Equ,2005,18(9):961-990.
[10] DA IQ Y,FU Y X,GU Y G.Existence and uniqueness of positive solutions of semilinear elliptic equations[J].Science in China A,2007,50(8):1141-1156.
[11] G IDASB,SPRUCK J.A priori bounds for positive solution of nonlinear elliptic equations[J].Comm PartialDiff Equ,1981, 6(8):883-901.
[12] CHEN Y Z.Parabolic partial differential equations of second order[M].Beijing:University Press,2003.
[13] WEISSLER FB.Existence and non-existence of global solutions for a semilinear heat equaiton[J].IsraelJMath,1981,38(1-2):29-40.
Threshold Result for Sem il inear Parabolic Equations
DA I Q iu-yi*,GU Yong-geng,L IU Fang,X IE Jun-hui
(College ofMathematics and Computer Science,Hunan NormalUniversity,Changsha 410081,China)
The initial boundary value problem of semilinear parabolic equations is studied.It is proved that any positive solution of its steady-state problem is an initial datum threshold for the existence and nonexistence of global solution to the associated parabolic problem(see Theorem 1 for the precise statement).
initial boundary value problem;semilinear parabolic equation;steady-state problem; threshold result
O175.26
A
1000-2537(2011)02-0007-09
2010-09-24
国家自然科学基金资助项目(10971061);湖南省研究生创新基金资助项目(CX2010B209)
*通讯作者,E-mail:daiqiuyi@yahoo.com.cn
(编辑 沈小玲)

