空间直线方程的解题探讨
陈淑贞
(海南师范大学 数学与统计学院,海南 海口 571158)
空间直线方程的解题探讨
陈淑贞
(海南师范大学 数学与统计学院,海南 海口 571158)
介绍了空间解析几何中求空间直线方程的各种方法.通过实例研究了求直线方程的不同解法和解题思路,以培养学生分析问题、解决问题及综合应用知识的能力.
解析几何;空间直线;方程;分析法
1 引言
在空间解析几何中,空间直线是其主要内容之一[1].由于空间直线方程的表示方式有多种,因而求空间直线方程的解题思路、解题方法和技巧也不相同.对同一道题,如果从不同的角度去分析,采用不同的处理方法,则得到不同的解法,通过比较,可选择出最优的解题方法.本文主要通过实例研究求空间直线方程的各种解题方法和解题思路,以达到培养学生分析问题、解决问题及综合应用知识的能力,从而启发学生的创新能力.
求空间直线方程的解题方法主要有以下四种:
1)通过求直线上的两点得到直线方程.
2)通过求直线上的一点及方向向量得到直线方程.
3)通过求过直线的两个平面得到直线方程.
4)利用空间平面直线束方程得到直线方程.
利用空间平面直线束方程求解直线方程,是一种实用、有效而简洁的方法.
定义设L1、L2是两相交的空间直线,通过L1、L2的交点并属于L1、L2所在平面的全部直线叫做由L1、L2所确定的空间的平面直线束.

2 空间直线方程求解方法

都相交的直线方程.
分析1因为所求直线过点P,所以只要求出直线上的另一个点即可得直线方程.由L1、L2的方程,易知L1与L2相交,且P点不在L1、L2所确定的平面上,所以所求直线过L1、L2交点,由此得解法1.
解法1易验证L1与L2相交,且P点不在L1、L2所确定的平面上,解L1与L2的方程得交点为M(1,2,3),所以所求直线方程为
下面通过实例研究空间直线方程的解法.
例1求过点P(1,1,1)且与两直线

分析2因为所求直线过点P,所以只要求出直线的一个方向向量,就可得直线方程.由于所求直线与L1和L2都相交,由此既可求得直线的一个方向向量,从而得解法2.
解法2设所求直线的方向向量为={X,Y,Z},那么所求直线L的方程可写成:


分析3因为L1与L2相交,且P点不在L1、L2所确定的平面上,所以所求直线为P与L1所确定的平面和P与L2所确定的平面的交线,由此得解法3.
解法3因为L1与L2相交,且P点不在L1、L2所确定的平面上,L1又过点M1(0,0,0),所以P与L1所确定的平面的方位向量为

分析1因为所求直线过点P,又和已知直线相交,所以只要求出所求直线和已知直线的垂直交点即可得直线方程,由此得解法1.

分析2因为所求直线过点P,所以只要求出直线的一个方向向量,就可得直线方程.由于所求直线与L1垂直相交,由此既可求得直线的一个方向向量,从而得解法2.

分析3因为L1与所求直线垂直相交,且P点不在L1上,所以所求直线为P与L1所确定的平面和过P且垂直L1的平面的交线,由此得解法3.

分析4因为点P不在L1上,点P与L1可唯一确定一个平面,而所求直线又在这个平面上,所以可构造这个平面上的直线束方程,然后利用平面直线束方程求出直线方程,从而得解法4.
解法4首先构造P点与L1确定的平面的平面直线束,在直线L1上取两点P1(1,-1,5),P2(-1,0,2),则直线PP1和PP2确定的平面直线束方程为:


分析2直线过点P,又平行于已知平面且和已知直线相交,所以可求出直线的一个方向向量,从而得直线方程,由此得解法2.
解法2设所求直线的方向向量为={X,Y,Z},因为它平行于平面x-2y+z-1=0,所以有:


分析3由条件所求直线为P与已知直线确定的平面和过P平行于已知平面的平面的交线,由此得解法3.
解法3由题意所求直线在P与已知直线确定的平面上,同时也在过P平行于已知平面的平面的上,而P与已知直线确定的平面方程为:

分析4因为所求直线在点P和已知直线确定的平面上,所以可构造这个平面上的直线束方程,然后利用平面直线束方程求出直线方程,从而得解法4.
解法4首先构造P点与已知直线确定的平面的平面直线束,在已知直线上取两点P1(1,1,0),P2(-1,0,1),则直线 PP1和PP2确定的平面直线束方程为:

分析1由已知条件可求出射影直线上的两点,从而得直线方程,即有解法1.
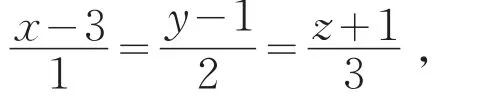
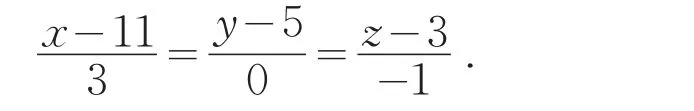
分析2可通过求已知直线L与平面π的交点和所求直线的一个方向向量,得到直线方程,由此得解法2.
解法2已知直线L与平面π相交,可解得其交点为M(11,5,3),设所求直线的方向向量为:={X,Y,Z},则有与平面π的法向量垂直,以及与平面π的法向量、直线L的方向向量共面,所以有
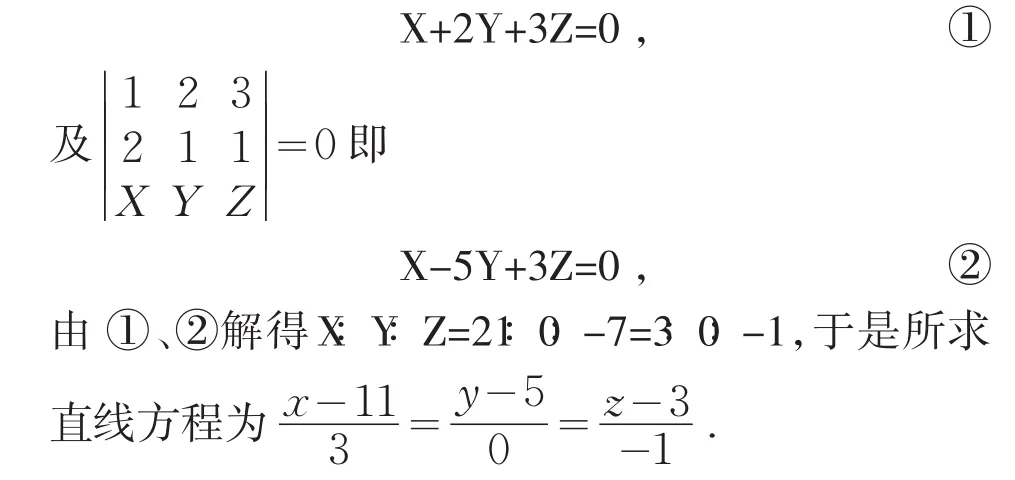
分析3所求直线在平面π上,又在过L且垂直于平面π的平面上,由此可得解法3.
解法3过L且垂直于平面π的平面方程为

分析4因为所求直线在过L且垂直于平面π的平面上,所以可构造这个平面上的直线束方程,然后利用平面直线束方程求出直线方程,从而得解法4.
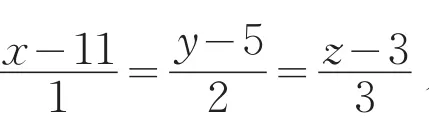

在以上空间直线方程的各种解法中,我们看到有些方法较传统,求解过程冗长,有些方法思路清晰,过程简洁,有些方法具有独到与新颖之处.从各题的解法中,学生可比较找出每道题的最优解题方法,从而加深了学生对空间直线的理解,也提高了学生分析问题、解决问题和综合运用知识的能力.
[1]吕林根,许子道.解析几何(第四版)[M].北京:高等教育出版社,2006.
[2]彭放.空间的平面直线束及其应用[J].高等数学研究,2000,3(1):8-10.
Investigation of Solving Spacial Line Equation
CHEN Shuzhen
(
College of Mathematics and Statistics,Hainan Normal University,Haikou571158,China)
This paper presents several methods to solve spatial line equations.In order to cultivate student’s potential of analyzing problems,solving problems and comprehensive ability to apply the theory knowledge,some different meth⁃ods and approaches were showed to solve linear equations in several examples.
analytic geometry;spatial line;equation;analytical method
O 182
A
1674-4942(2011)03-0348-04
2011-04-26基金项目:海南省自然科学基金(110004)
毕和平

