五维混沌Chen系统的电路实现及其控制方法分析

黄 露，唐驾时

（湖南大学 机械与运载工程学院，湖南 长沙 410082）

五维混沌Chen系统的电路实现及其控制方法分析

黄 露，唐驾时

（湖南大学 机械与运载工程学院，湖南 长沙 410082）

在研究Chen系统的基础上，通过增加两个状态环节，新构建了一个五维混沌系统.提出了基于Mathmatic环境下的模型仿真以及EWB电路仿真软件下的电路设计过程.并对该五维系统采取了自适应反馈控制，有效地控制了系统的混沌.从理论分析、数学计算以及模拟电路实现等方面，分析该系统的基本动力学行为，并证实它具有一定的实用价值.

混沌系统；Chen系统；自适应反馈控制；EWB；Lyapunov理论

近年来，混沌问题的研究是非线性科学领域的热点问题之一[1].混沌理论在许多工程领域得到了广泛的应用，比如图像加密，保密通讯，信息工程等等，其具有巨大的潜在应用价值[2-3].高维混沌系统具有更加复杂的动力学性质，目前，已经研究和发现很多的高维混沌系统[4-7].如四维的超混沌Lorenz系统[8]，四维超混沌Chua系统[9]，四维超混沌Chen系统[10]等等.因为在非线性电路中，高维混沌系统的应用具有更高的能力与效率，所以对高维混沌系统的研究的确具有实际价值.

美国加利福尼亚大学伯克利分校的蔡少堂教授提出了一个三阶自治混沌电路，即蔡氏电路[11]，由于该电路结构简单，动力学特性明显，且数学上的研究已经得到充分证明，并且具有很好的非线性特性，因而得到了广泛的关注.越来越多的混沌系统都通过电路得到了实现.混沌现象存在于各式各样的电路系统中，混沌的电路实现是实现混沌的基本方法之一.其对于研究非线性系统的动力学特性，证明混沌吸引子的存在与否，验证混沌控制与同步方法等等方面起到很重要的作用.Chen利用混沌反控制的方法发现了Chen系统，此系统是一个三维的混沌系统.本文通过在Chen系统中增加两个新的状态变量，构建了一个五维的混沌系统，并且通过电路的仿真得到实现.同时在系统中增加两个控制器k1和k2，采用自适应反馈控制方法对该系统的混沌进行控制，使系统的混沌过程达到所期望的效果.

1 系统构建及特性分析

Chen系统描述见式（1）

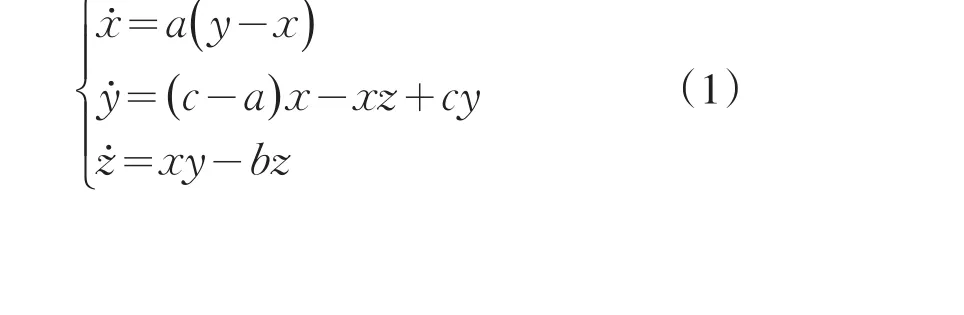
其中a、b、c均为实参数，a=35，b=3，c=30时，该系统处于混沌状态.采用状态反馈的方法，在此系统中增加两个反馈控制器w和v，这样就能得到一个五维的混沌Chen系统.系统描述见式（2）：

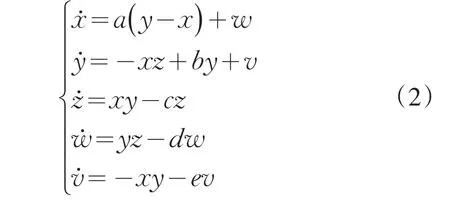
其中，x、y、z为系统的变量，w和v为反馈控制器的状态变量，常数a、b、c为系统参数，d和e为控制的增益.当a=35，b=12，c=3，d=0.1，e=4时，该系统有一个典型的混沌吸引子.此系统是一个典型的五维混沌系统，其非线性项均为二次项.该混沌系统的构建是合理的，并且其具有复杂的动力学特性.由系统（2）得到式（3）：

计算得到：-a+b-c+d-e=-35+12-3-0.1-4=-30.1＜0，系统（2）为耗散系统.这就意味着，当t→0时，系统的轨线最终渐近到一个特定的零体积元，即一个吸引子上.为求解系统（2）的平衡点，令方程的各项都等于0，求解得到其中的一个平衡点S0=（0，0，0，0，0）.在平衡点S0处线性化系统（2）得到Jacobian矩阵为：

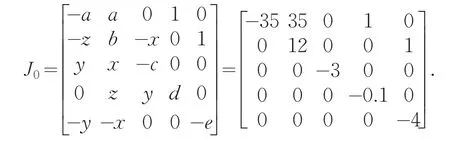
由det（J0-λI）=0，得到其特征根方程.解特征根方程，得到对应平衡点S0处的特征值为 35，12，3，0.1，4.第二个特征值为正数，其余为负数，因此，平衡点S0为一个不稳定的鞍点.

混沌吸引子相邻轨线之间呈现彼此排斥的趋势，并以指数速率相分离，而Lyapunov指数可以用来定量描述轨线间彼此排斥和吸引的量[11].通过计算得到系统（2）的 Lyapunov指数[12]：LE1=0.30283，LE2=-0.06843，LE3=-0.068970，LE4=-4.035782，LE5=-25.954088.可以看出，其中有一个正的Lyapunov指数，因而可以知道，该五维系统处于混沌状态.

2 数值仿真

利用Mathmatic分析软件，得到系统（2）在x-w，z-w等平面的相图见图1.

图1 x-w,z-w各平面的相图Fig.1The plane phase diagram of x-w,z-w

3 电路仿真设计

为了验证这个五维混沌系统的混沌动力学行为，本文采用模拟电子电路的方法对该系统进行振荡器电路的设计.电路设计采用的是EWB仿真软件，该电路由线性电阻R，线性电容C，乘法运算器AD633，运算放大器NE5534组成.NE5534是一种高速低噪声单运算放大器，其压摆率可以达到13 V/μs，有着较大的电压范围，供电电压可以从V到20 V.此外，NE5534的管脚与LM741兼容，是代替LM741的理想选择.

从前面的分析我们可以知道，由于该混沌系统方程必须在x，y，z，v，w分别取初值1，1，1，0，0的时候，系统才能进入混沌状态.因此，在设计电路时，必须给电容C1，C2，C3赋初值，该电路才能进行振荡.具体作法如下：我们通过一个双路的单刀双掷开关和一个外接1.5 V的电源对电容充电，然后再把电容接入电路中.通过这一过程，该混沌电路就能进行振荡.具体电路图见图2.

根据混沌系统电路原理图，可以得到以下方程式（5）:

图2 混沌系统电路原理图Fig.2 The circuit principle diagram of Chaos system

电路的具体参数取值如下：C1=C2=C3=C4=C5=0.01 μF，R1=R6=R27=10 kΩ，R2=350 Ω，R7=350 Ω，R3=R8=R9=R11=R16=R17=R19=100 kΩ，R24=R25=120 kΩ，R10=300 Ω，R15=10 Ω，R18=400 Ω，R23=350 kΩ，R26=350 kΩ，R26=300 kΩ，R28=400 kΩ，R4=R5=R12=R13=R20=R21=R22=R29=R30=1 kΩ.

电路仿真实验结果见图3，与图1的仿真结果相比较，可以看出结果基本一致.所以仿真结果是有效的.

图3 电路仿真实验中各平面相图Fig.3The plane phase diagram of circuit simulation experiment

由于EWB软件采用的是实际电路元件模型，所以其仿真实验和实际电路的实验应该是基本符合的.通过上面的理论分析以及仿真实验结果，可以证实本文构建的非线性系统（2）确实是一个五维的混沌系统，它显示了混沌系统所具有的各种特性.由于该系统可以用振荡电路来实现，因此，实际应用中，通过构建PCB板，可以将该系统运用到工程应用中.

高维的混沌系统具有更加复杂的混沌特性，相对于三维的混沌chen系统，五维混沌chen系统在保密通信、信息加密等方面的作用更大.而且电路构建简单，实现并不复杂，因此该系统的构建是合理与现实的，具有一定的实用价值.

4 自适应反馈控制

混沌系统的控制，按其控制方式有反馈混沌控制与非反馈混沌控制两种类型.其目的是通过恰当的方法和途径，有效的抑制系统的混沌行为，使得李雅普诺夫指数下降到期望的水平，通过对系统的控制获得工程实际中需要的新的动力学行为.一般情况下，通过在系统中增加控制器来实现对系统的控制.所以，选择恰当的控制器，就能对混沌系统进行有效的控制.而控制器的选取，要求必须在原有的基础上，对系统的影响尽可能小.

混沌的控制方法有很多，现在采用比较多的有：OGY控制法；自适应控制法；连续控制法等等.目前对chen系统的控制研究是一个热点问题，人们已经采用了很多方法对chen系统进行了有效的研究，这些方法有自适应反馈控制、微分反馈控制、线性反馈控制等等.

本文将采用自适应反馈控制法，对构建的五维混沌系统进行控制.自适应反馈控制方法是通过控制目标响应与实际响应之间的差值来调节系统的参数，从而使系统的实际响应与目标响应能达到近似同步的控制方法.在控制系统的运动过程中，系统不断的识别被控制的状态和参数，并将系统当前运行的得到的指标与实际期望的指标加以比较.进而得到系统的误差值，反馈给输入环节，调节控制器的参数，使得系统逐渐稳定到实际期望的指标或者根据自适应的规律来改变控制作用，以保证系统运行在所期望指标下的最优或近似于最优状态.具体原理如下：首先，假设所研究的非线性系统产生混沌特性的动力学模型能够被构造出来，例如系统可以用逻辑映像来描述.其次，利用数学上的定量最小二乘法，设计一个参数估计器，使得估计器的参数改变与系统的混沌行为无关.但是可以通过改变估计器的参数来实现对所假设的动力学模型的参数进行回归估算.然后，利用所估算的参数模型算出系统的适当的输入量，逐次调整，使系统的混沌过程达到所期望的周期信号.只有当它达到所期望的参考信号时，控制器才起作用，从而实现了对所需周期信号的有效控制.该自适应控制方法具有很多优点，它并不局限于离散系统，对连续系统同样适用.自适应反馈控制方法也适合控制多参数的非线性系统，精度高，可以保持较小的转变时间.

本文将通过对新构建的五维chen混沌系统中增加两个控制器，来实现对混沌系统的自适应反馈控制.在系统（2）中增加两个控制器k1和k2，得到受控系统见式（5）：

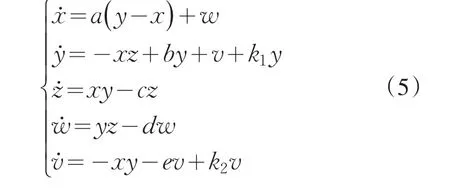
根据Routh-Hurwitz定理，系统稳定的充要条件是其特征根均具有负实部.通过计算求得特征根λ1=-a=-35，λ2=b+k1，λ3=-c=-3，λ4=-d=-0.1，λ5=-e+k2.其中λ1、λ3、λ4都小于零，因此只要满足b+k1＜0，即可以使得系统在S0（0，0，0，0，0）趋于稳定.所以当k1＜-b，k2＜4时，该五维chen系统线性化后的到的特征方程的根均具有负实部.数值仿真中，未加控制器时得到系统的在x-t和y-t处的时域图见图4.

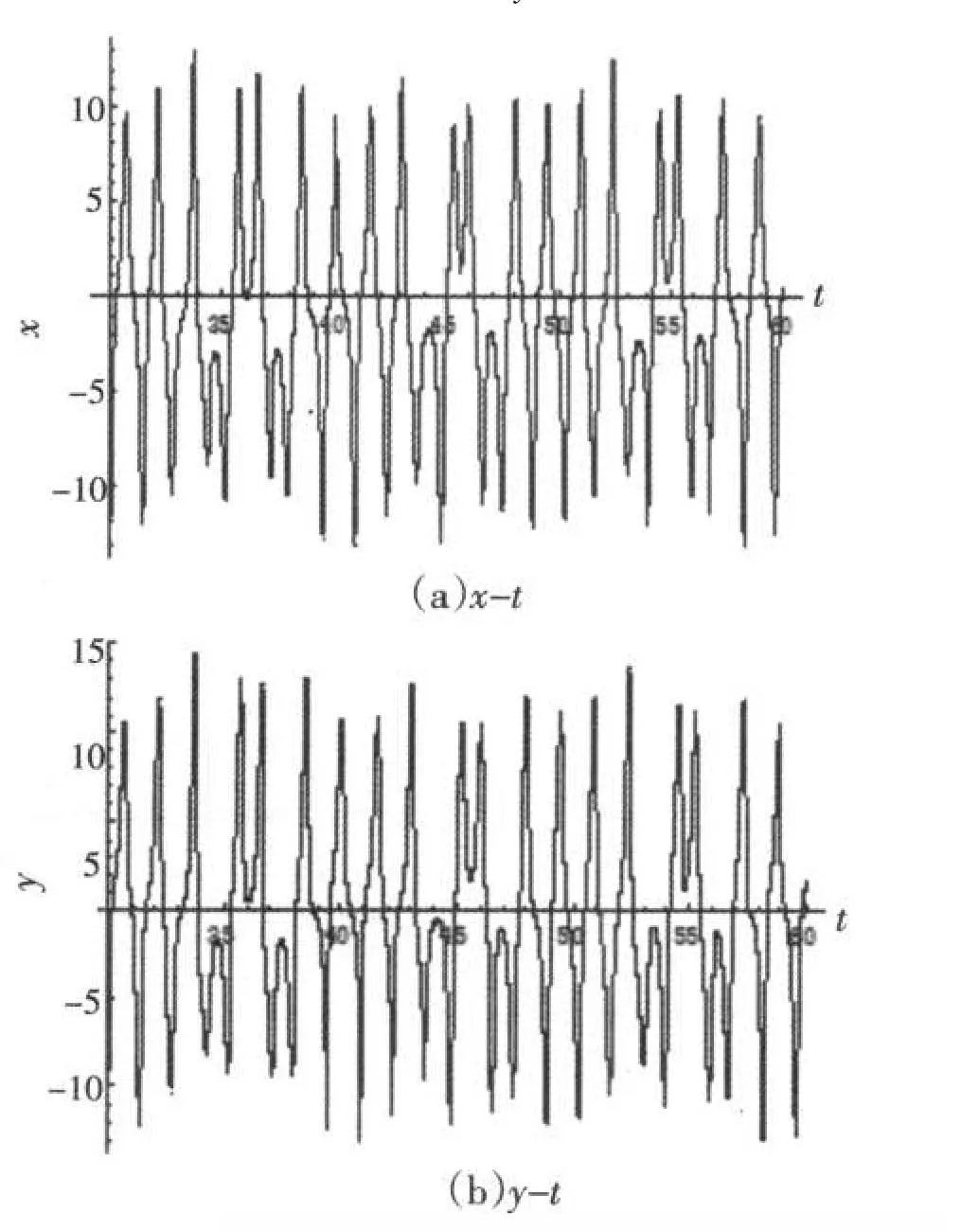
图4 x-t、y-t时序图Fig.4 Timing diagram of x-t、y-t

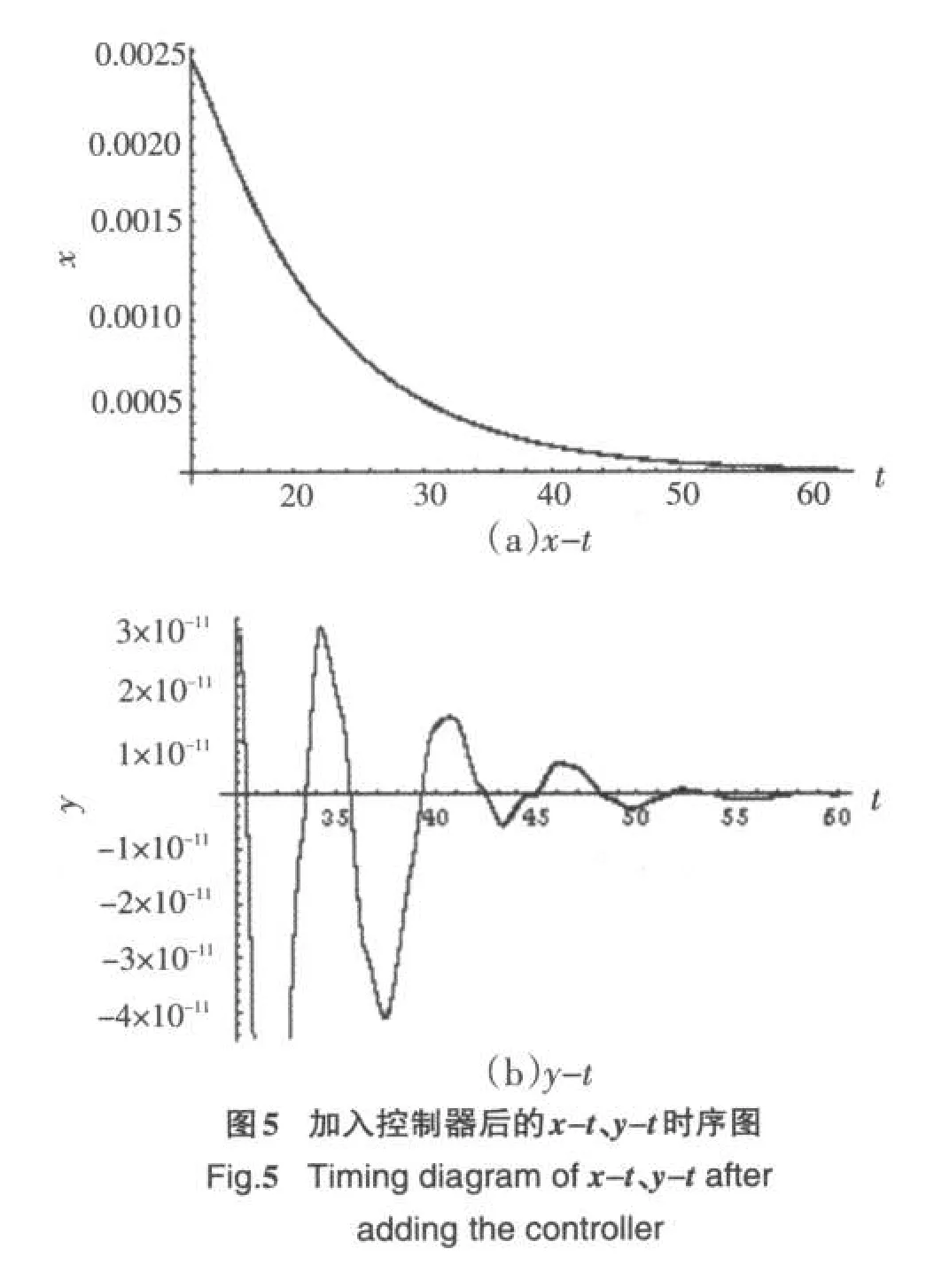
加入控制器k1和k2后，当k1取值-13，k2取值 3时，数值仿真得到的时域图见图5.

相比之下，可以看出控制效果十分明显，说明该控制器的选取是合理的.自适应反馈控制中，可以看出控制器的参数k1和k2的选取与参数a、c、d无关，只要求k1＜-b，k2＜e便可以控制到平衡点S0，数值试验结果验证了理论的正确性.

这里介绍的自适应反馈控制混沌的方法有效的控制chen混沌系统，对该五维chen系统的稳定性分析和仿真表明，多变量的反馈能更加有效的控制混沌到平衡点，与单变量的自反馈控制相比较增加控制器的维数可以改善和提高控制的效能.

5 结论

本文对新构建的五维混沌Chen系统的混沌特性和复杂的动力学行为进行理论分析，包括Lyapu⁃nov指数、平衡点、相图、时序图等等.运用EWB软件设计了一个非线性电路，进行了电路模拟仿真，证实了此系统的混沌行为.

1）使用Mathmatic，对新构建的系统进行分析计算，理论上证明了该系统为混沌系统.

2）在理论可以证明的基础上，利用模拟电路的振荡器原理，采用放大器、电阻和电容来实现信号的起振，设计了一个振荡电路，来实现电路的混沌现象.

3）利用自适应反馈控制方法，在系统中增加两个反馈控制器k1和k2，使得系统的混沌现象得到有效控制.并得出结论，多变量对改善系统的混沌和提高控制效能更加有效.

本文在原有的Chen系统基础上，构建了一个五维系统，并实现了系统的混沌吸引子.由于此系统能用实际电路来实现，故具有一定的实用价值.

[1]王光义,郑艳,刘敬彪.一个超混沌Lorenz吸引子及其电路实现[J].物理学报,2007,2:78-83.

[2]陈关荣,吕金虎.Lorenz系统族的动力学分析,控制与同步[M].北京:科学出版社,2003.

[3]王东升,曹磊.混沌、分形及其应用[M].合肥:中国科学技术出版社,1995.

[4]Cenys A,Tamasevicius A,Baziliauskas A,et al.Hypercha⁃os in Coupled Colpitts Oscillators[J].Chaos,Solitions&Fractals,2003,17:351-355.

[5]Cafagna D,Grassi G.New 3D-scroll Attractors on Hyper⁃chaotic Chua’s Circuit[J].Internationl Journal of Bifurca⁃tion and Chaos,2003,13:2900-2905.

[6]Thamilmaran K,Lakshmanan M,Venkatesan A.A Hyper⁃chaos in a Modified Canonical Chua’s Circuit[J].Interna⁃tional Journal of Bifurcation and Chaos,2004,14:218-225.

[7]Tanaka N,Hiroshi O,Masayoshi N.Estimating the ampli⁃tude of measurement noise present in chaotic time series[J].chaos,1999,9:436-445.

[8]Ning C Z,Haken H.Detuned Lasers and the Complex Lorenz Equations:Subcritical and Super-Critical Hopf Bi⁃furcationgs[J].Physical Review A,1990,41:3826-3837.

[9]Kapitaniak T,Chua L O.Hyperchaotic Attractor of Unidi⁃rectionally Coupled Chua’s Circuit[J].International Jour⁃nal of Bif-urcation and Chaos,1994,4:477-482..

[10]Chen G,Dong X.From chaos to order:methodologies,perspectives andapplications[J].World Scientific Pub Co,1998,2:132-142.

[11]Chua L O.The Genesis of Chua’s Circuit[J].J Archiv fur Elektronik and Ubertragungstechnic,1992,46(4):250-257.

[12]张玉兴,赵宏飞,向荣.非线性电路与系统[M].北京:机械工业出版社,2007.

Analysis of Circuit Realization and Controlling Method of the Fifth Dimension Chen System

HUANG Lu，TANG Jiashi
（
College of Mechanical and Vehicle Engineering，Hunan Uuniversity，Changsha410082，China）

Based on the study of Chen systems,a new fifth dimensional chaotic system was built by adding two control links.It introduced model simulation under Mathmatic condition and the circuit designing process under EWB condition.It used the feedback system to control the fifth dimension system and effectively controlled the system of chaos.The ba⁃sic dynamic behaviors of the system were studied with theoretical analysis,mathematical calculation and simulation cir⁃cuit implementation.Some certain practical value has been confirmed.

chaotic system；Chen system；adaptive feed-back control；EWB；Lyapunov theory

O 322

A

1674-4942（2011）03-0283-05

2011-04-20

国家自然科学基金资助项目（11172093）

黄 澜