基于岭回归法对海南省住宅销售价格的影响因素的研究

林 晓，张靖宇，胡晓华

（海南师范大学 数学与统计学院，海南 海口 571158）

基于岭回归法对海南省住宅销售价格的影响因素的研究

林 晓，张靖宇，胡晓华

（海南师范大学 数学与统计学院，海南 海口 571158）

利用多元线性回归模型，研究了1996年到2008年海南省住宅销售面积、人口及城镇居民可支配收入对海南省住宅销售价格的影响，基于岭回归法来解决自变量间多重共线性的问题，借助EVIEWS 6.0和SPSS17.0软件，建立相关的数学模型，最后预测海南省2009年住宅销售价格，结果表明模型短期预测精度较高.

多重共线性；多元线性回归模型；岭回归

海南建省以后，房价就一直迅速飙升，特别当国家宣布把海南岛建设成国际旅游岛后，海南省的商品住宅房房价就以更加惊人的速度在提高.因此，有必要对海南商品房的房价和所受的影响因素做一个简略的分析.以1996年至2009的《中华人民共和国统计年鉴》和《海南统计年鉴》的相关数据做为依据[1]，部分数据是笔者以上述两部统计年鉴的相关数据计算出来，见表1.从商品住宅房的销售面积、海南省人口总数、海南省城镇居民可支配收入3个方面作为自变量来构建模型（住宅消费价格=住宅销售额/住宅销售面积），进行实证分析.

1 基本模型简介

岭回归是由A.E.Horel在1962年提出的一种能统一诊断和处理多重共线性的问题的特殊方法，设线性回归模型为[2-3]：

参数β的最小二乘估计为：

如果解释变量之间存在多重共线性，亦即|X′X |≈0.但是，岭回归是给加上一个正常数矩阵 λI(λ＞0),λ为单位阵，那么构造(X′X+ λI)-1使得|X′X+λI |的可能性比| X′X |≈0的可能性更小.从而，有效地避免了因| X′X |≈0造成的方差变大，故岭回归估计为

称为的岭回归估计，β()λ为β岭回归参数，当λ=0，，就是普通的最小二乘法估计.当λ→∞,所有的系数估计值都向零趋近，一般在（0，1）之间取值.

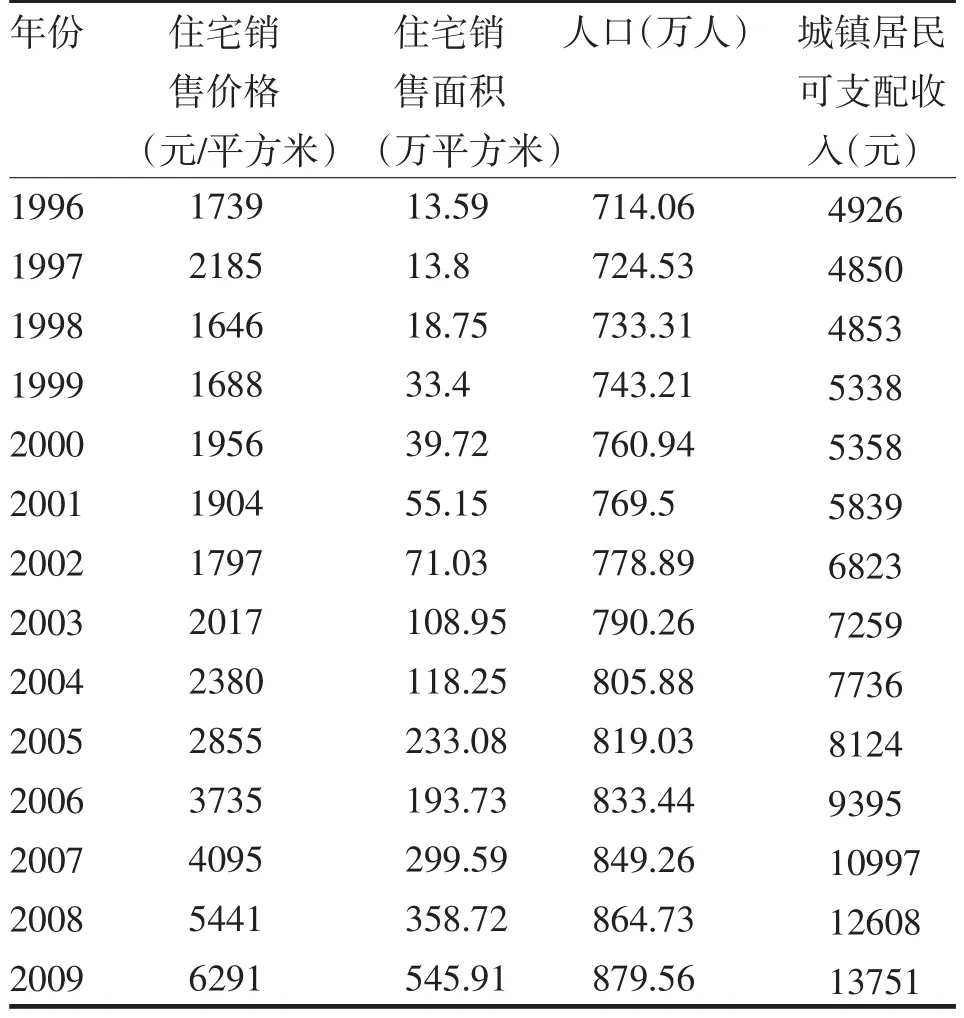
表11996-2009年海南省商品住宅房房价的相关数据[1]Tab.1 Related data of the residential sales price of Hainan province in 1996-2009

2 实证分析

为了减少舍入误差，在估计时，对表1中的所有变量进行自然对数处理，利用最小二乘法,做多元线性回归：

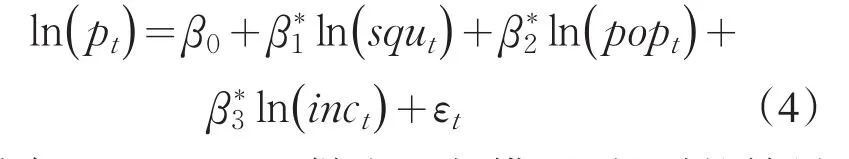
我们用Eviews6.0做出回归模型，得到的结果如下：

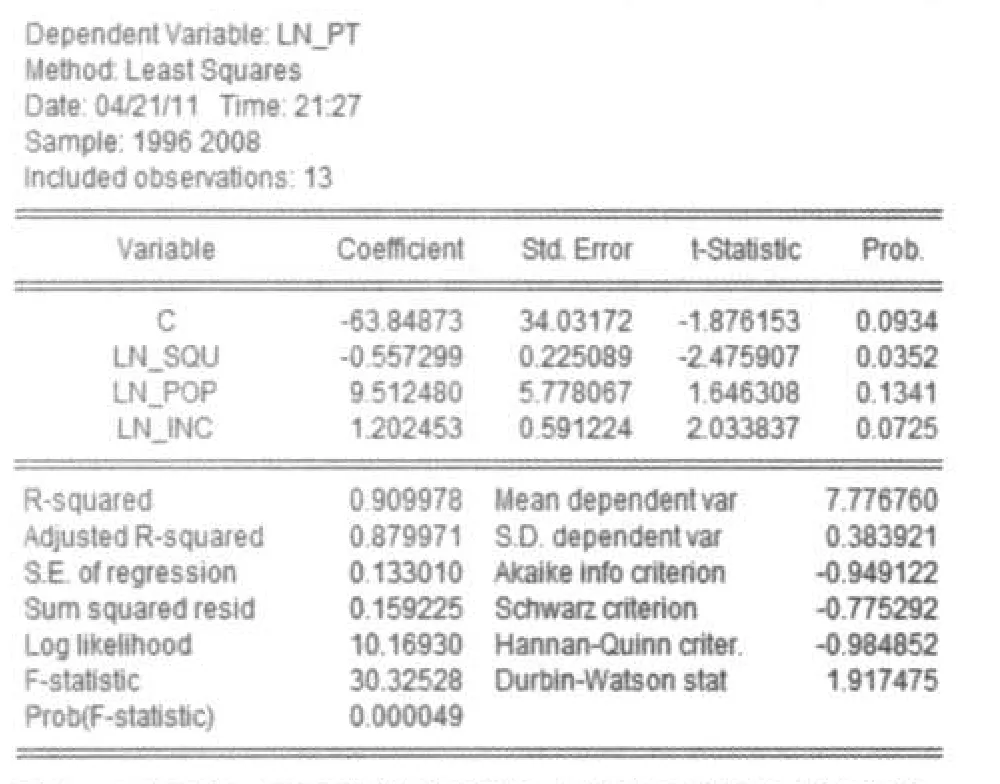
图11996年-2008年数据所建立的多元线性回归模型的参数估计与统计量Fig.1 The estimations and statistics of multiple linear regression model parameters in 1996-2008

由图1可看出，可决定系数和调整的可决定系数不是特别的高，分别为0.909978和0.879971，但在可以接受的范围；除了自变量ln（squ）的t统计量在0.05的水平下是显著的，其余自变量的t统计量在0.05的水平下是不显著的；F统计量为30.32528，在0.05水平下，拒绝原假设，我们可以认为是显著的，即所有变量对方程的拟合较好.残差也服从正态分布态，符合古典线性回归模型的要求，见图2.

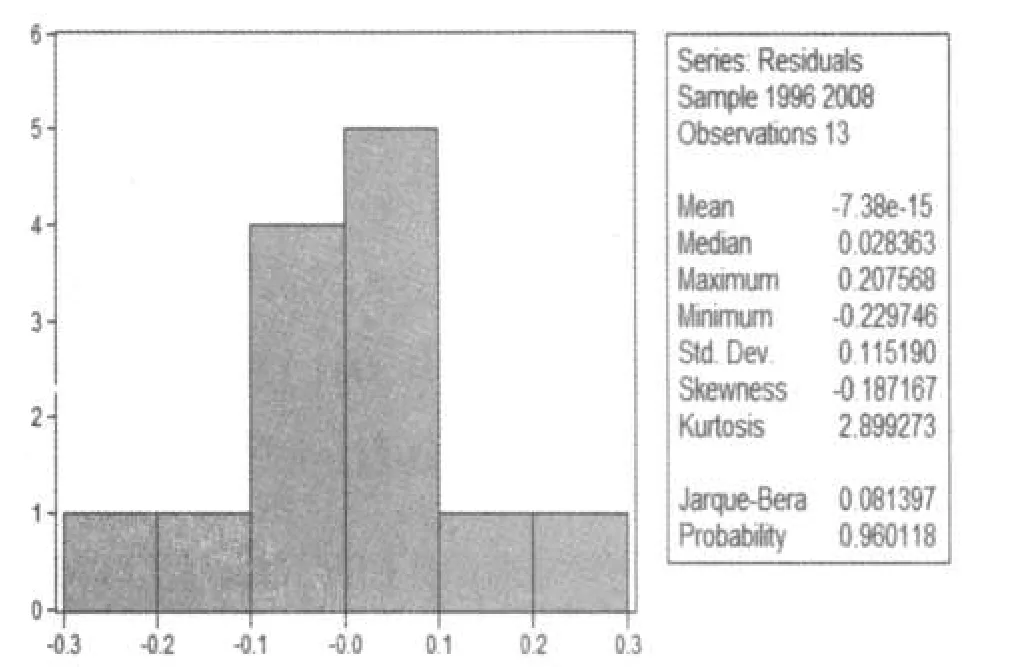
图2 残差序列的基本统计量Fig.2 Basic statistics of residual series

但是，我们可以看到ln（squ）这个自变量的系数符号是负的，住宅面积和住宅每平方米的价格呈负相关关系并不符合常识，于是推测自变量间存在共线性的关系.通过检测自变量间的相关关系，得到的结果见表2.

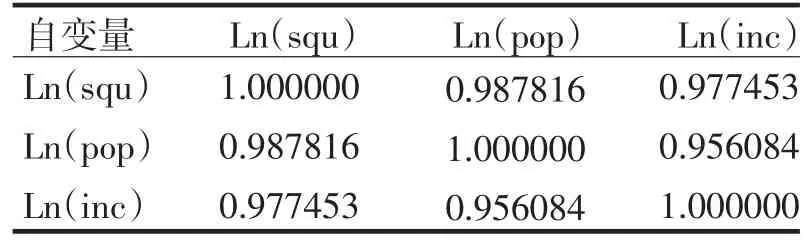
表2 自变量间的相关系数Tab.2 The correlation coefficients of the independent variables

从表2可以看出自变量之间是高度相关的，证明了自变量之间多重共线性的存在.而用Spss 17.0也检测出自变量之间也存在多重共线性，见图3，一般VIF＞10，我们就认为自变量之间存在多重共线性[3].

在众多解决多重共线性的方法中，岭回归是一个特别有用的方法.

我们把3个影响因素样本与住宅消费价格样本用岭回归建模如下[4]：利用Spss17.0，我们令k从0到1，步长为0.02，做出岭迹图（见图4）.

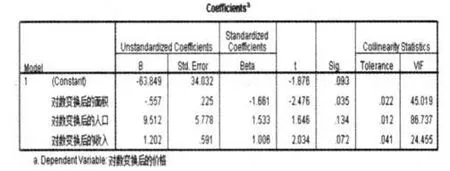
图3 自变量间的多重共线性检验Fig.3 Multicollinearity test of independent variables

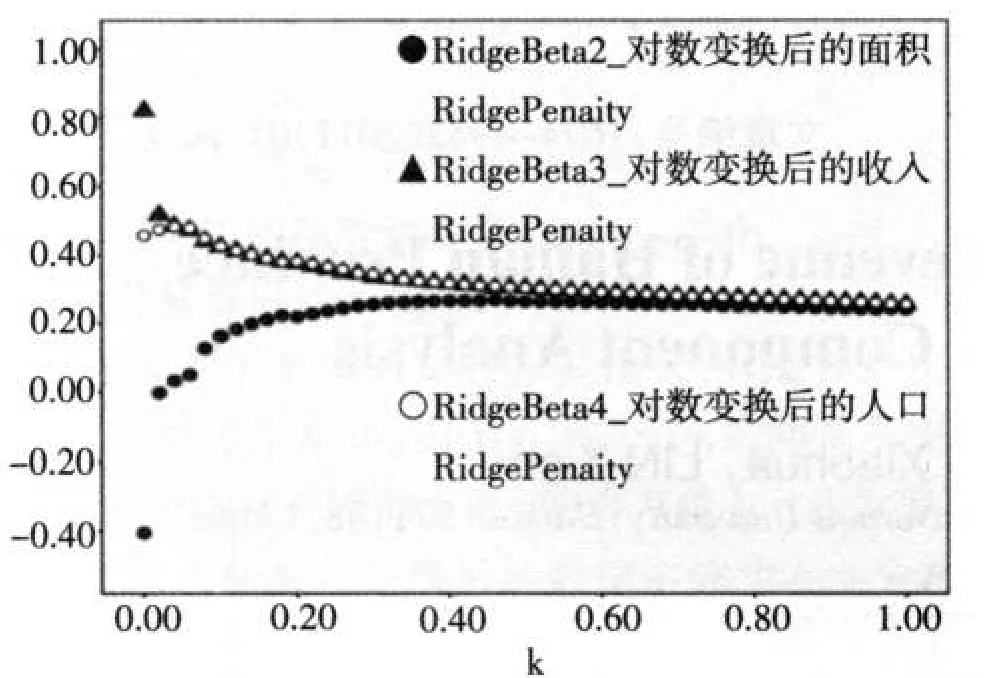
图4 岭回归路径图Fig.4Ridge trace

通过图4，我们发现k在0.38左右时候，岭迹曲线趋于稳定，即k在大于等于0.38后，岭回归系数稳定.我们令k=0.38做岭回归，得到了标准化变量估计式：

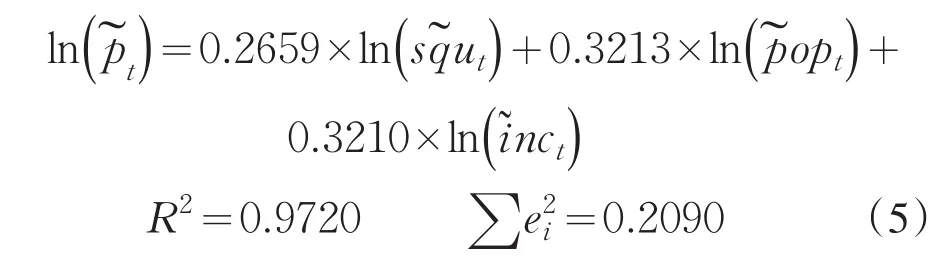
我们把式（5）转化为非标准化变量估计式：

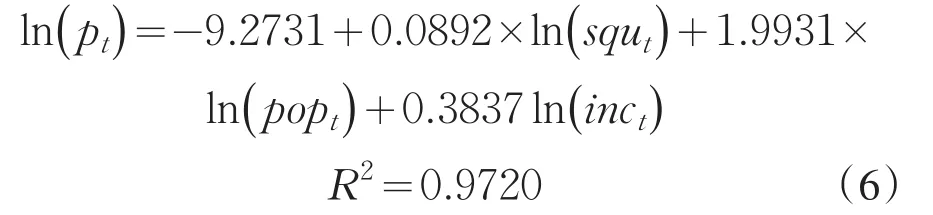
回归方程的可决定系数等于0.972，表示在样本数据中，因变量的97.2%可由这三个自变量（线性）来解释，同时说明估计的回归方程函数较好地拟合了样本数据.岭回归拟合效果明显，成功消除了多重共线性的影响，并且自变量3个因素的系数均为正数，与常识相符.通过式（6），我们可以预测2009年的住宅销售价格对数化后的情况.

3 结论

我们将2009年的相关数据代入到式（6）中，得到2009年的的预测值为8.457371，而真实值为8.746875，相对误差的绝对值为3.3%，准确率为96.7%，误差在可接受的范围之内，岭回归模型的预测效果是比较理想的[5].计算Theil不等系数为0.016827，预测精度比较高，也从另一方面说明了预测效果是理想的.

首先，从岭回归的结果来看，所有自变量都与应变量成正相关关系；三个自变量中按回归系数大小而排列的顺序（由大到小）：ln（pop）t＞ln（inc）t＞ln（squ）t.由此可知，在这个模型中，对应变量影响最大的是自变量ln（pop）t，在其他自变量不变的情况下，当 ln(p opt)每增加1%，应变量就会提高1.9931%.海南其独特的地理位置吸引了大量的人员来旅游，尤其是在国家宣布把海南建设成国际旅游岛后，更多人口涌入，购房数量随之增大.其次，在其他自变量不变的情况下，ln(i nct)每增加1%，应变量就会增加0.38%，与农村居民相比，城镇居民的可支配收入更具灵活性，而可支配收入的投资选择也很多，投资商品房就是其中之一；最后，商品住宅房面积的对数变换是三个自变量中影响应变量最小的，在其他自变量不变的情况下，每增加一个单位，会引起0.0892%的应变量的提高，这是因为住房是一个长期消费的物品，我们认为住房的销售面积很难使得消费者在短期内接受大户型的购买，故这个自变量是影响最小的.

[1]Howie中国统计年鉴[EB/OL].[2011-04-11].http://www.stats.gov.cn/tjsj/ndsj.

[2]王文博.计量经济学[M].西安:西安交通大学出版社,2004:107

[3]易丹辉.数据分析与Eviews应用[M].北京:中国人民大学出版社,2008:63.

[4]陈昊,林寅.基于岭回归的京郊农民收入之影响因素分析[J].商场现代化:上旬刊,2010(7):100-102.

[5]邹奉元,丁笑君,潘力丰.青年女子提醒的特征指标及岭回归预测研究[J].纺织学报,2006,27(4):56-59.

Research on the Residential Sales Price of Hainan Province Based on the Ridge Regression

LIN Xiao，ZHANG Jingyu，HU Xiaohua
（College of Mathematics and Statistics，Hainan Normal University，Haikou571158，China）

Using the multiple linear regression,the effect of residential sales area,population and disposable income of urban residents on the residential sales price of Hainan province in 1996-2008 was studied,the multicollinearity of inde⁃pendent variable factors was solved by the ridge regression.By using the EVIEWS 6.0 and SPSS17.0,the related mathe⁃matical model was established to predict the residential sales price of Hainan province in 2009,and the prediction accu⁃racy is ideal.

multicollinearity；multiple linear regression；ridge regression

O 29

A

1674-4942（2011）03-0257-03

2011-04-18

毕和平