基于二进制偏移载波(BOC)调制方式的卫星导航技术研究*
张 怡,张西凯,陈利民
(西北工业大学电子信息学院,西安 710072)
0 引言
目前,传统的GPS系统主要采用BPSK调制方式,信号经BPSK调制后信号能量主要集中在载频附近,其传输效率较低,抗干扰性能较差。随着GPS系统的不断升级和改善,最新一代的GPS系统加入了新的BOC调制信号[1],以此满足新时期导航站的需要,实现新一代的高精度空基导航系统。BOC调制技术的基本思想是对BPSK基带信号使用一种类似信源编码[2]的处理方法,从而使其频谱产生适当偏移。新的调制方式需要有新的捕获方法与之相适应,文中就此针对新的BOC调制信号的直接捕获[3]技术进行了研究,并进行了相应的仿真试验和分析。
1 BOC调制信号的技术原理
所谓二进制偏移载波(BOC)调制信号,是以一个方波作为子载波,对卫星产生的扩频码信号进行辅助调制,在这之后再调制到主载波上,即用扩频信号s(t)和一个频率为 f s的方波副载波相乘,这使得信号的频谱分裂[4]成两部分,且分列于主载波频率的左右。BOC调制信号的主要特点是信号功率并不是调制到载波频率的主瓣上,而是调制到了载波频率两侧的旁瓣上,且这两个旁瓣之间的间隔为副载频宽度的两倍[5]。
BOC调制信号主要由两个参数来描述:副载波频率和传播的码元速率,用符号表示为BOC(m,n),其中m表示副载波频率为fs=m×fbase,n表示码率为fc=n×fbase,式中的 fbase=1.023MHz是基带频率。
BOC调制信号的技术原理框图如图1所示。

图1 BOC调制信号技术原理框图
BPSK调制信号,也称为二进制移相键控,是受键控的载波相位按基带脉冲而改变的一种数字调制方式。其信号形式的一般表达式为:

式中:T s为码元间隔;g(t-nT s)为脉宽为T s的矩形脉冲序列;w c为载波频率,an为第n个信息符号所对应的电平值,其相应的统计特性为:

式中P为事件出现的概率。相比较而言,BOC调制基本原理是在原有的BPSK调制基础上,再增加一个二进制副载波进行调制。以正弦调制为例,其表达式为:

式中:c(t)为码序列波形,表达式为c(t)=Σkckh(tkT c),ck为第k个码片的电平值,h(t-kT c)为码元间隔为Tc的非归零码脉冲序列;fs为副载波频率;sign为符号函数。
2 BOC调制信号的频谱特性
随着我国北斗(compass)系统、美国GPS系统、欧洲Galileo系统和俄罗斯GLONASS系统以及其他系统的开发和应用,有限的导航频率成了稀缺资源,多系统之间的兼容性和互操作性成为了一个日益重要的问题。BOC调制信号的出现能很好的解决这一问题。
BOC调制信号能够将共用一个发射频率的信号频谱分开,实现共用载波频率条件下的频谱分离。与BPSK调制方式有所不同,BOC调制信号可以实现频段共用,同时实现频谱分离,具有更好的相关函数性能,以及良好的相关和抗干扰特性。它的功率谱有主瓣和副瓣,而且主瓣的能量主要集中在副载波频率上,主瓣数与在主瓣之间的副瓣数之和等于n1,这里n1=2f s/f c。
以正弦BOC调制信号的归一化功率谱为例,当n1为偶数和奇数时的归一化频谱密度表达式分别表示为:
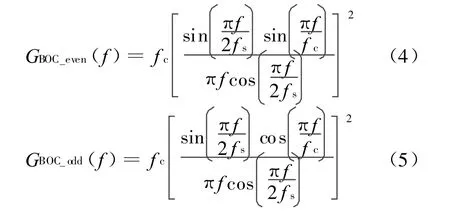
由上式可以看出n1为偶数和奇数时的BOC调制信号的功率谱形式上的差别只是:前者是正弦函数,而后者是余弦函数。n1为奇数时的BOC调制信号的功率谱在中央有一个旁瓣,n1为偶数时则没有。当副载波 fs=10.23MHz,同时扩频码速率为 fc=5.115MHz,则调制信号可以表示为BOC(10,5),功率谱函数特性图如图2所示。与图2功率谱特性图相对应的自相关函数图如图3所示。


由图3可知,与传统的BPSK信号相比,BOC调制信号的自相关函数具有更窄、更尖锐的相关峰,相关特性更加优良,但由于新的自相关函数包含多个峰值,也就是说除了主峰之外还有多个副峰,多峰结构的出现会对信号的捕获产生模糊,采用单边带处理法可以在一定程度上消除其负面影响。
总的说来,BOC调制信号的使用,将信号能量更多的集中在所占带宽的边缘部位从而增加了信号的有效带宽,相应的噪声方差也得到了改善,在信道噪声和抗干扰方面可以获得比原有BPSK更好的性能。通过频谱搬移,使得现有信号占据了不同的频带,这有效的减少了BOC信号与其它导航信号在公共频带上的相互干扰。
3 BOC调制信号的直接捕获
3.1 传统的单边带处理法
所谓单边带直捕方法,即是对一个边带作单独处理的方法,和BPSK信号调制时的处理方法一样,只是频率中心在一个副载波上,且码速率就是BOC调制时的f c。由于边带处理的是扩频码速率为 f c、带宽比BOC调制信号窄的BPSK调制信号,相应的相关函数也就比双边带BOC调制宽,这样宽的相关函数可明显的降低采样速率。
简要来说,单边带直接捕获的基本原理为:先对接收信号进行降频处理,再分别对上边带和下边带都进行带通滤波处理,然后用本地发生器生成本地伪随机码和副载波信号,并以相同的采样频率进行副载波调制处理(可以保证本地码片与副载波信号的起始相位相同),再利用处理后的接收信号与本地信号进行相关运算并作滤波处理;最后对上下边带的相关结果进行非相干的处理,选取相应的最大比例峰值作为捕获结果,并对此进行捕获判决。
3.2 改进的单边带均值法
单边带均值法的原理框图如图4所示。

图4 单边带均值法
单边带均值法是以循环相关理论为基础的一种快速直接捕获方法。它是将接收信号伪码序列和本地伪码序列中的每N个点分别依次进行均值处理而构成新的序列,之后两个新序列同时进行循环相关处理。当出现高于判决门限的相关峰值时,就可判断出接收信号的码元所在的具体均值码段进而确定其确切位置。在同样的FFT计算量下,可将时间不确定范围扩大为原来的N倍;相应地,在不改变时间不确定范围情况下,可以减少FFT计算量,缩短捕获时间。
4 仿真结果分析
在MATLAB平台上对传统的单边带处理法和改进的单边带均值法分别进行仿真,输入信号为BOC(10,5)调制的扩频信号,两种方法均采用1024点FFT,处理过程中中频频率为20.48MHz,采样频率为81.92MHz,均值点数为4。同时考虑到噪声的影响,在信噪比分别为-5dB和-15dB的输入噪声情况下分别进行仿真比较,其仿真结果如图5和图6所示,横坐标为相关点个数,纵坐标为相关峰值。
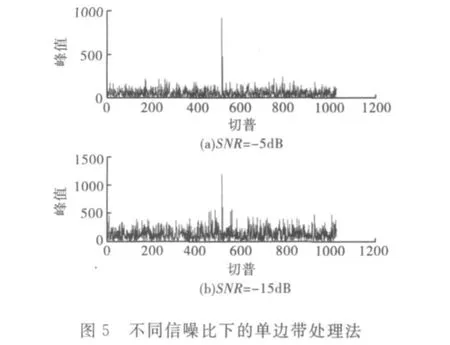
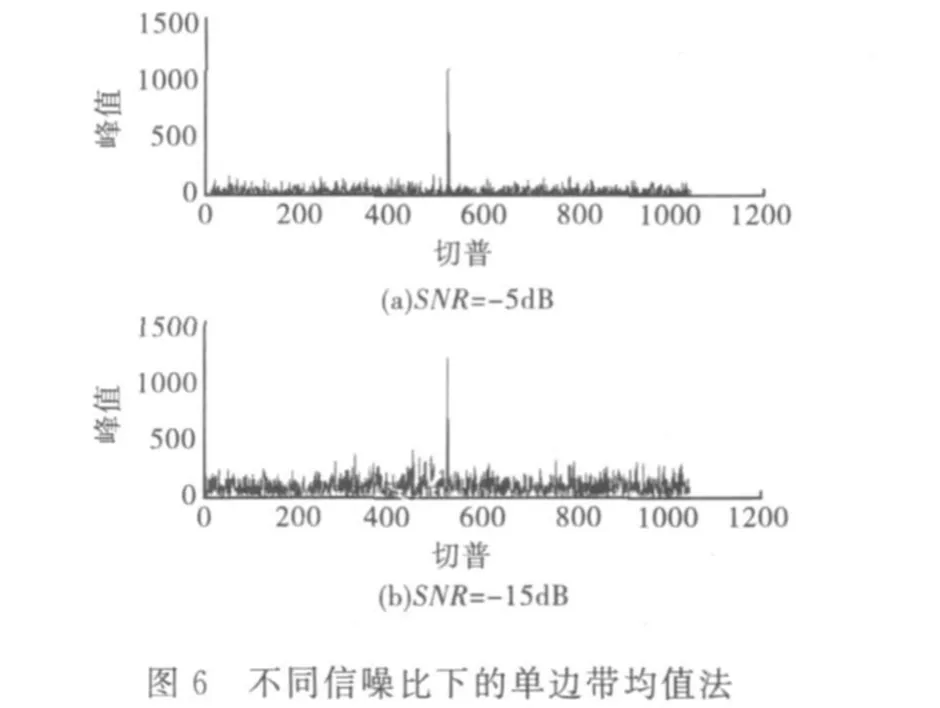
由图5和图6可见,经过捕获处理后,结果有明显相关峰值,采用传统的单边带处理法在不同信噪比下最高峰值无明显差异,而采用改进的单边带均值法在不同信噪比下峰值有所不同,在信噪比为-15dB的情况下最高峰值比信噪比为-5d B高,这表明采用单边带均值法通过信号的相应处理能有效的减小噪声的影响,得到更为明显的相关结果,减小误捕的概率,增大捕获精度,且可以锁定捕获码片误差在1个码片范围内,频率误差控制在20Hz范围内。
5 结论
仿真结果表明,与传统的单边带处理法相比,采用改进的单边带均值法对BOC调制信号进行直接捕获,在同样的FFT计算量下可以有效扩大时间不确定度的搜索范围,并将伪码误差控制在1个码片范围内,有效减小噪声干扰,使捕获精度得到了有效提高。另一方面,在不改变时间不确定范围的情况下,可以减小FFT运算量,极大地缩短捕获时间,提高捕获效率。文中提出的新算法适应了现代卫星导航发展对于新调制方式技术提出的新要求,是一种快速有效的BOC调制捕获算法。
[1] Lohan Elena Simona,Burian Adina,Renfors Markku.Lowcomplexity unambiguous acquisition methods for BOC-modulated CDMA signals[J].International Journal of Satellite Communications and Networking,2008,26(6):503-522.
[2] Rebeyrol Emilie,Macabiau Christophe,Lestarquit Laurent,et al.BOC power spectrum densities[C]//Proceedings of the Institute of Navigation,National Technical Meeting,2005:769-778.
[3] 张琳,初海彬,张乃通.卫星导航信号长码快速直接捕获算法研究[J].通信学报,2007,28(3):120-124.
[4] Harris RB,Lightsey E G,A general model of multipath error for coherently tracked BOC modulated signals[J].Selected Topics in Signal Processing,IEEE Journal,2009,3(4):682-694.
[5] 曾兴雯.扩展频谱通信及其多址技术[M].西安:西安电子科技大学出版社,2004.
[6] Nunes Fernando D,Sousa Fernando M G,Leitao Jose M N.Gating functions for multipath mitigation in GNSS BOC signals[J].IEEE Transactions on Aerospace and E-lectronic Systems,2007,43(3):951-964.

