尖头刚性弹贯穿金属厚靶的终点弹道性能研究*
李小笠,陈小伟
(1南京工程学院工程基础实验与训练中心,南京 211167;2中国工程物理研究院结构力学研究所,四川绵阳621900)
0 引言
穿甲效应主要是指弹丸或破片对靶板的侵彻与贯穿。对于金属靶板,又以延性扩孔(高速尖细弹丸)和剪切冲塞(低速钝头弹丸)等形式最为常见。对厚靶的穿甲可以分为侵彻和贯穿两种情况,侵彻时弹靶间的相互作用并没有传到靶板背面,而贯穿时弹丸头部与靶板作用产生破坏机理最终导致弹丸在靶板上产生穿孔。穿甲的破坏机理与弹丸头部形状、撞击速度、靶板材料性质以及靶板厚度和尺寸有关。
延性扩孔模型可以用球形(SCET)或柱形(CCET)空腔膨胀理论近似简化为一维问题。在刚性弹侵彻力学研究中,动态空腔膨胀模型是公认的最有效理论分析方法之一。
文中基于文献[1-3]的理论工作,根据侵彻阻力的一般表达式,结合量纲分析、球形动态空腔膨胀模型及相关实验分析,在已提出的撞击函数I、弹头形状函数N和无量纲靶厚χ三个无量纲物理量之外,引入无量纲阻尼函数ξ,应用于刚性尖头弹垂直贯穿金属厚靶中。同时给出了刚性尖头弹贯穿金属靶板的弹道极限速度和剩余速度的解析表达式,研究并讨论了阻尼函数ξ的应用范围及其作用效应。分析表明,这四个无量纲物理量几乎可以完全表征刚性尖头弹在不同速度下对金属靶板穿甲的实验数据。
1 无量纲阻尼函数ξ
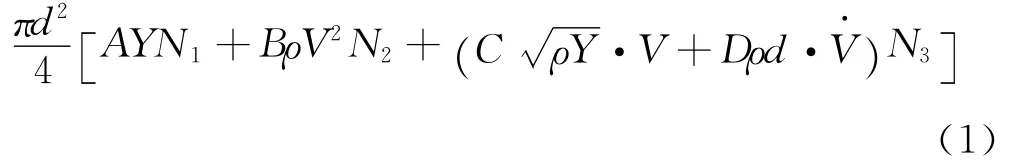
弹丸头部表面轴向侵彻阻力:Fx=式中:d是弹丸直径;Y是靶材屈服强度;ρ是靶材密度;A、B、C、D都是靶板的无量纲材料常数。形状系数N1、N2和N3是与弹丸头部形状和摩擦系数有关的无量纲数,用于描述侵彻过程中刚性弹头部形状的影响[1]。方程右边第三项是粘性项,最后一项是由于弹丸高速侵彻的减速度效应产生的附加质量项。
陈小伟等[1]在撞击函数I和弹头形状函数N 两个无量纲物理量之外[2-3],提出并定义了控制侵彻过程的第三个无量纲数,即无量纲阻尼函数ξ:

由此可知,仅有3个无量纲物理量,即撞击函数I、弹头形状函数N和阻尼函数ξ,完全可以控制刚性弹的无量纲侵彻深度X/d,X是侵彻深度。
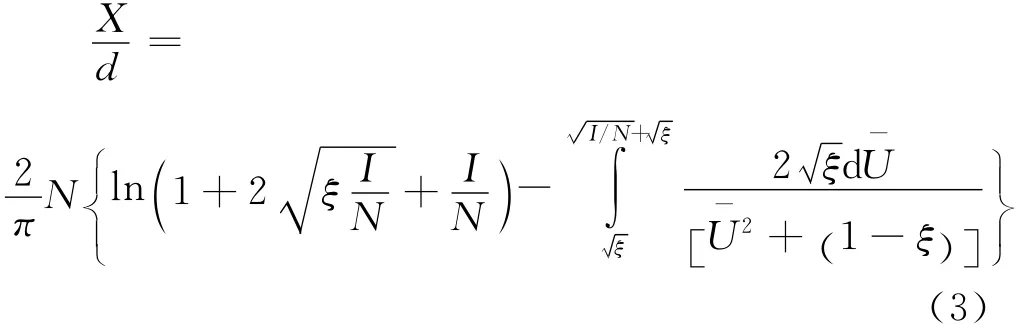
工程应用中,式(3)仅在0≤ξ<1时成立,对应的无量纲侵彻深度有:
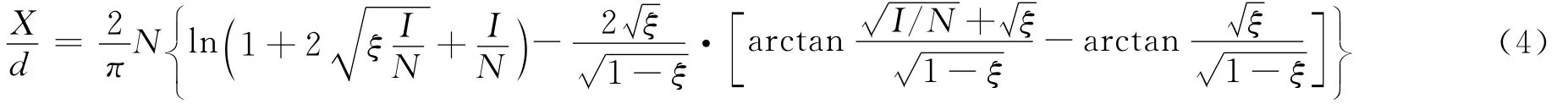
2 尖头弹对厚靶的穿甲
设无量纲靶厚χ=H/d,其中H是靶板厚度。假设韧性扩孔为唯一的侵彻机理,弹尖到达厚靶背面即视为贯穿,贯穿后的剩余速度是Vr。忽略靶板背面的边界效应,由式(4)可得到无量纲靶厚χ的表达式:

式中:Ir是对应于剩余速度Vr的撞击函数,其表达式是弹丸计及附加质量项后的弹体修正质量。当弹丸以弹道极限速度VBL撞击厚靶时,Vr=0,式(5)有:
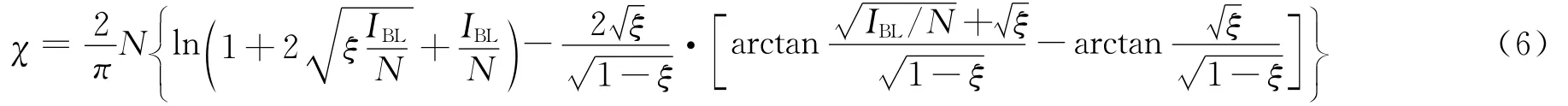

由式(6)可求解弹道极限速度VBL。由超越方程式(7)可解出Ir,进一步可得剩余速度Vr。
当ξ=0时,即不考虑侵彻过程中弹靶阻尼作用。由式(6)和式(7)可以分别得到弹道极限速度VBL和剩余速度Vr的简化表达式,与文献[1]一致。
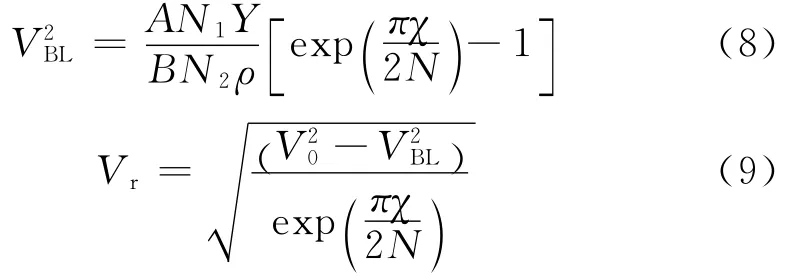
尖头刚性弹的几何函数N足够大,而其穿甲金属靶的初速相对较小,因此撞击函数I值较小,近似有I/N→0。已有的实验数据都表明,大多数情况下,阻尼函数ξ较小,对于金属靶,0.01<ξ<0.1,对终点弹道性能有近15%的影响。因此可进一步简化,由式(6)和式(7)可以求出弹道极限速度和剩余速度的表达式。
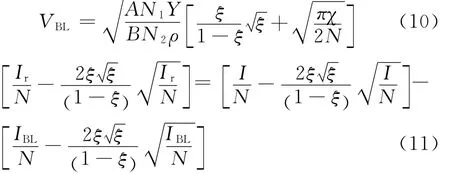
若ξ<0.01,可忽略阻尼函数ξ,即ξ=0则式(10)和式(11)可进一步简化为:
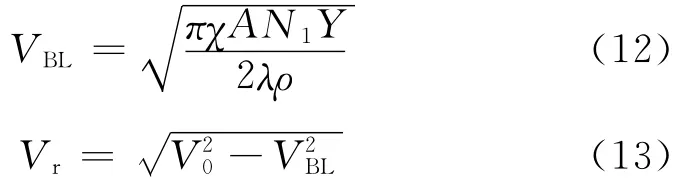
式中,V0是弹丸撞靶初速。
3 实验分析
本节针对已公开发表的侵彻实验数据,利用文中的理论结果和已有的研究工作[4]进行比较分析。所采用的实验数据均在刚性弹假设范围内。根据3个无量纲量I、N和ξ的定义,将文献[5-8]中的所有实验数据进行重新组合整理。
图1~图5给出不同实验结果和理论分析的比较。一般而言,伴随初始撞击速度的增加,不同模型对剩余速度的预期总是逼近实验值,即在高速撞击区,无量纲阻尼函数ξ和附加质量项的影响可以忽略。这是可以理解的,在弹道极限附近,弹体动能几乎完全消耗,主要用于临界穿甲;进一步增加初速,弹体动能绝大多数伴随弹体贯穿而出,因此任何合理的终点弹道分析模型,其剩余速度的分析曲线应是实验结果的渐近线。因此对模型的分析,更应集中在终点弹道极限附近。
由图1~图5可知,引入ξ相当于相应提高靶板的抗侵彻能力,终点弹道极限较之文献[4]相对增加。但若考虑附加质量,终点弹道极限则会下降,甚至小于文献[4]的分析值,而更接近终点弹道极限的实验值;附加质量有助于提高弹体的侵彻能力。因此,无量纲阻尼函数ξ和附加质量项对侵彻/穿甲的作用是相反的,相互补偿,因此同时计及ξ和附加质量项的分析预期与文献[4]更接近。需指出的是,对于尖头刚性弹侵彻金属厚靶的情形,可认为附加质量项对于剩余速度的影响甚微,可忽略之;这是由式(7)决定的,根据文献[1]的分析,I/N(包括Ir/N 和IBL/N)与弹体计及附加质量项后的修正质量无关。
另一方面,尽管包括粘性效应和附加质量项的侵彻阻力一般表达式已提出数十年,已有动态空腔膨胀模型可用于相应确定粘性项系数C,但如何确定附加质量项系数D仍未见有已知工作。因此,文献[1]没有进一步讨论附加质量项在侵彻中的作用。文中试图通过拟合实验结果值来反演附加质量项对侵彻/穿甲的影响。由图1~图5可知,在同时计入粘性项条件下,若弹体质量增加5%~10%,包括弹道极限和剩余速度的终点弹道性能理论预期与实验结果符合较好。换言之,可认为实际应用中,附加质量项对弹体质量的贡献大体在5%到10%左右,进一步由公式Mm可以推导出D值的范围,D值大约在1~2之间。
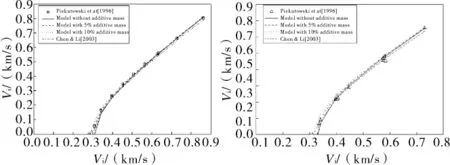
图1 参[5]剩余速度的理论预期和实验结果(正撞击)
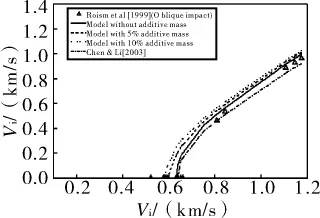
图2 参[5]剩余速度的理论预期和实验结果(斜撞击)
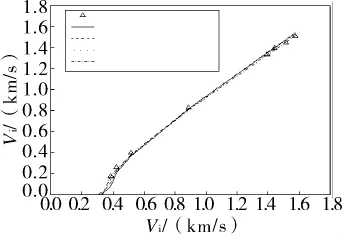
图3 参[6]剩余速度的理论预期和实验结果(斜撞击)
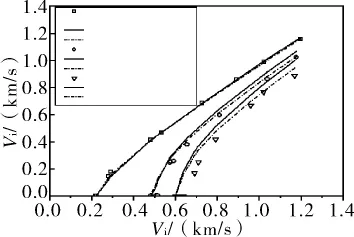
图4 参[7]剩余速度的理论预期和实验结果(正撞击)
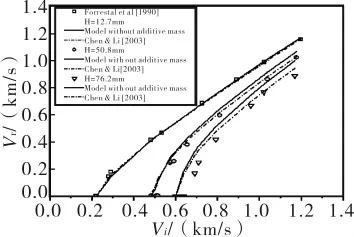
图5 参[8]剩余速度的理论预期和实验结果
4 结论
根据侵彻阻力的一般表达式,文中建立尖头刚性弹垂直贯穿金属厚靶的分析模型。根据动态空腔膨胀理论,给出了由4个无量纲物理量,也即撞击函数I、弹头形状函数N、阻尼函数ξ和无量纲靶厚χ=H/d表示的终点弹道性能表达式。结合公开发表的贯穿实验数据,将相关分析与不计阻尼函数ξ情形的异同进行了比较,分析结果与实验数据相符。同时进一步定量讨论了因减速度效应导致的附加质量项对贯穿/侵彻的影响。
[1]陈小伟,李小笠,陳裕泽,等.刚性弹侵彻力学中的第三无量纲数[J].力学学报,2007,39(1):77-84.
[2]Chen XW,Li QM.Deep penetration of a non-deformable projectile with different geometrical characteristics[J].Int J Impact Eng,2002,27(6):619-637.
[3]Li QM, Chen XW.Dimensionless formulae for penetration depth of concrete target impacted by a non-deformable projectile[J].Int J Impact Eng,2003,28(1):93-116.
[4]Chen XW,Li QM.Perforation of a thick plate by rigid projectiles[J].Int J Impact Eng,2003,28(7):743-759.
[5]Piekutowski AJ,Forrestal MJ,Poormon KL,Warren TL.Perforation of aluminum plates with ogive-nose steel rods at normal and oblique impacts[J].Int J Impact Eng,1996,18(7/8):877-887.
[6]Roisman IV,Weber K,Yarin Al,Hohler V,Rubin MB.Oblique penetration of a rigid projectile into a thick elastic-plastic target:theory and experiment[J].Int J Impact Eng,1999,22(7):707-726.
[7]Rosenberg Z,Forrestal MJ.Perforation of aluminium plates with conical-nosed rods-additional data and discussion[J].J Appl Mech Trans ASME,1988,55(1):236-238.
[8]Forrestal MJ,Luk VK.Perforation of aluminium armor plates with conical-nose projectiles[J].Mech Mater,1990,10(1/2):97-105.

