射流推力矢量喷管粒子沉积特性数值模拟*
宋亚飞,高 峰,曾 华,文 科
(空军工程大学导弹学院,陕西三原 713800)
0 引言
火箭发动机推力矢量技术可以提高导弹的机动性和突防能力,在航空航天领域具有广泛的应用。根据实现方法,推力矢量装置大致可分两类:机械调节式推力矢量控制和流体推力矢量控制。射流推力矢量(fluidic thrust vectoring,FTV)通过引入二次射流使喷管主流发生偏转以产生矢量推力。与机械式推力矢量喷管相比,射流推力矢量喷管以其结构简单、重量轻、易于维护、系统响应快、隐身性能好的优点成为国内外航空航天技术的热点。其中,激波矢量控制喷管是一种先进的采用流体控制推力矢量方向的新型矢量喷管方案,该方案是在喷管扩张段开孔或开缝,不对称的射入二次流,由二次流产生的激波迫使主流偏转,从而使喷管获得推力矢量偏转。
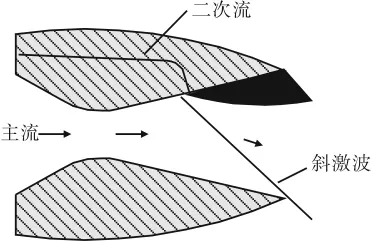
图1 激波矢量控制原理
20世纪90年代后期,NASA(美国航空航天局)兰利研究中心针对二元收敛 扩张喷管进行了一系列的流体控制方案试验和数值模拟[1-4]。国内对二次喷射流与主流干扰流场激波结构进行了不少风洞试验研究和数值模拟研究[5-10]。而关于两相流条件下射流推力矢量喷管研究的报道很少。文中以基于激波矢量控制的轴对称喷管为对象,采用粒子轨道模型对射流推力矢量喷管内的气固两相流动进行数值模拟,研究喷管中的粒子沉积问题。对射流推力矢量喷管的设计和工程实践具有一定的指导意义。
1 数学模型
假设固体火箭发动机射流推力矢量喷管内流场为定常的。对于粒子相为呈球形,采用粒子轨道模型,不考虑粒子的湍流扩散和化学反应,只考虑相间阻力和热泳力。
1.1 气相控制方程
气相控制方程可表示为如下形式:
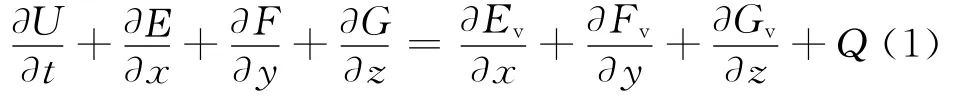
式中 :U 为守恒型变量,E、F、G 为守恒型通量,Ev、Fv、Gv为粘性通量,Q为粒子对气相产生的源项。
1.2 粒子相控制方程
粒子相的瞬时速度由下面的运动公式来确定:

式中:mp为粒子相的质量;Fp为拖曳力,Fp为:
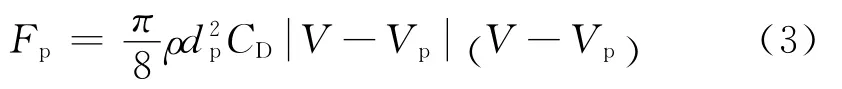
其中:ρ为气相密度;dp为粒子直径;CD为拖曳系数。粒子的位置可由以下公式计算:
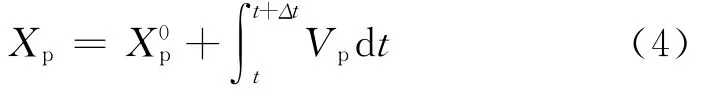
1.3 物理模型与网格划分
文中的计算使用三维轴对称矢量喷管模型,在直角坐标系下建立了结构化与非结构化混合网格,喷管的收敛段及二次喷射口采用COOPER技术生成结构化网格,喷管扩张段使用非结构化网格,网格结构如图2所示。
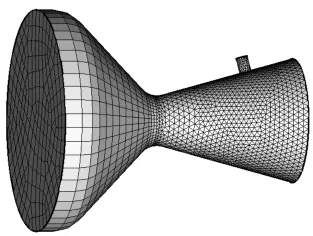
图2 计算网格
1.4 边界条件
1)气相边界条件:采用质量入口条件,在主、次流的入口边界上给定质量流率、总温、流动方向。出口采用压力出口,由于流动出口是超音速,各参数按二阶外推得到。自由来流马赫数为0。壁面为绝热壁,并采用无滑移边界条件。
2)粒子相边界条件:在喷管入口处,取入口处每个网格边的中点作为粒子的加入点。粒子的初始速度、温度及入射角和气相相同,粒子与壁面发生的碰撞为完全非弹性碰撞。
2 计算结果与分析
在喷管主流和二次流入口质量流率分别为2kg/s、0.01kg/s,总温均为3000K 的条件下,采用基于密度的隐式因子分解算法,求解连续相流场,达到收敛为止;采用粒子轨道模型对轴对称矢量喷管中气相和粒子相耦合计算。粒子直径范围为1~100μm,主流和二次流中粒子相的质量分数均为10%。
2.1 粒子浓度分析
图2是直径为5μm的粒子沿喷管对称轴的聚集浓度分布,可以看出粒子的聚集主要集中在喷管的收敛段和喉部附近。图3显示了直径分 别 为 1μm、5μm、10μm、20μm、50μm和100μm 的粒子加载时喷管内部的粒子浓度的分布情况。可以看出粒子聚集部位主要集中在喷管的收敛段和二次流入射口附近,随着粒子直径的增加,粒子高浓度区向喷管下游移动。粒子直径较小时(D=1μm),由于粒子的惯性小,随流性好,主流中的粒子从喷管入口流出,迅速汇人主流,与收敛段碰撞后也汇入主流,成扩散状态喷出,因此,粒子只在收敛段形成聚集。随着粒径的增加,由于粒子的惯性增大,粒子改变运动方向的能力减弱,粒子与壁面的碰撞加剧,粒子聚集部位逐渐向喉部移动,形成明显的粒子聚集带,粒径为100μm时喉部聚集浓度达到最大。由于二次射流喷射口直径较小,所以二次流中的粒子在入射口附近聚集浓度较高,粒子聚集带随粒子直径的增加而扩大,当粒子直径大于20μm时,粒子聚集带越过轴线,粒子直径为100μm时,二次流中的粒子在下壁面形成聚集。
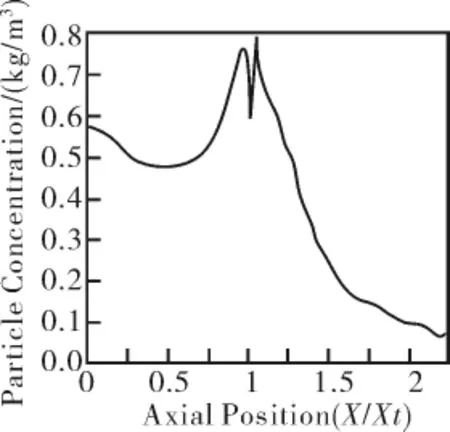
图3 对称轴上粒子浓度分布(D=5μm)
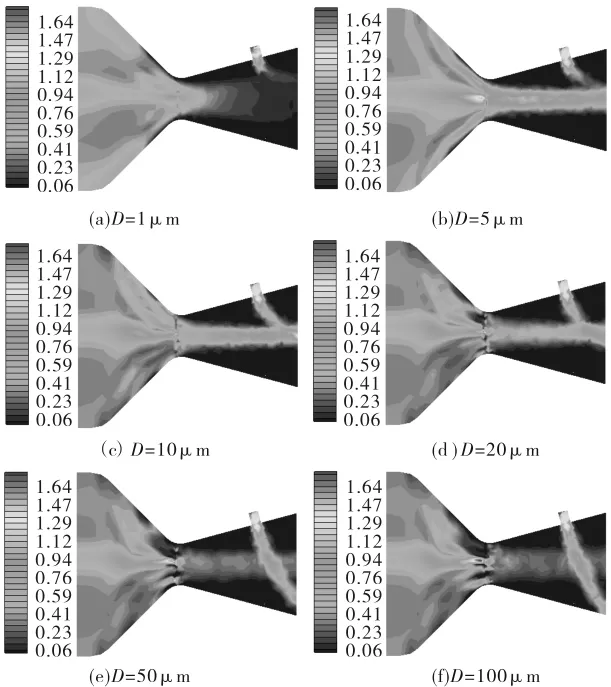
图4 喷管对称面粒子浓度分布 (kg/m3)
2.2 粒子沉积分析
图5显示了不同直径的粒子加载时喷管壁面的粒子沉积情况,当粒子直径为1μm时,喷管的收敛段的后部有粒子存在,但量很少。这主要是因为粒子质量小,随流性好,几乎能够分布于喷管的所有流动空间,只有部分与壁面发生碰撞,产生沉积;当粒子直径为5μm时,粒子在上游分布空间显著增加,单位面积的沉积率有所减小。直径从5μm增加到100μm的过程中,随着粒子惯性的增大,沉积率逐渐增加,但粒子的分布空间增加并不明显。当粒子直径为100μm时,二次射流中的粒子在下壁面发生沉积。另外,从图中还可以看出,粒子在喷管喉部的沉积率随着粒子直径的增大而增加。
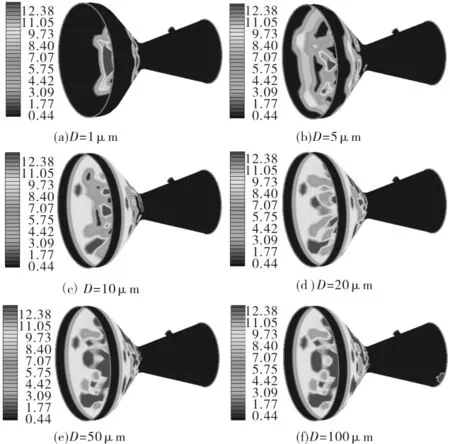
图5 喷管壁面的粒子沉积分布 (kg/m2·s)
为了能定量计算喷管中粒子的沉积率,将6组不同粒子在壁面的沉积率进行计算如表1所示,其中捕获率由以下公式计算:粒子捕获率=壁面捕获的粒子数/追踪的粒子总数
计算所得的最小沉积率为17.24%,最大为81.38%,小尺寸粒子发生沉积的几率很小,大尺寸粒子的沉积率较大,这与前面的分析结论相一致。
3 结论
文中利用粒子轨道模型对基于激波控制的轴对称喷管内气固两相流动进行了数值模拟,主要研究了固相粒子的沉积特性,比较了不同直径的粒子加入气相后喷管内部的粒子浓度分布和粒子沉积特征,定量研究了喷管内部的粒子沉积率。研究表明:
1)主流中粒子的沉积部位主要集中在喷管的收敛段和喉部附近。小尺寸粒子随流性好,与喷管壁面碰撞后很快扩散到气相中,仅在喷管收敛段的后部有沉积。大尺寸粒子在整个收敛段和喉部都有沉积,粒子直径越大沉积率越高。
2)二次流中的粒子形成的粒子聚集区随粒子直径的增加而增大,大尺寸粒子会在下壁面形成沉积。
3)喷管壁面的粒子沉积主要源于大尺寸粒子。减小燃气中的粒子尺寸可以有效减小粒子对壁面的烧蚀。
4)射流推力矢量喷管的热防护设计应考虑到二次流中粒子对壁面的烧蚀作用。
[1]Fariborz Saghafi,Afshin Banazadeh.Co-flow fluidic thrust vectoring requirements for longitudinal and lateral trim purposes,AIAA 2006-4980[R].2006.
[2]Jeffrey D Flamm.Experimental study of a nozzle using fluidic counterflow for thrust vectoring,AIAA 1998-3255[R].1998.
[3]Jeffrey D Flamm,Karen A Deere.Design enhancements of the two-dimensional dual throat fluidic thrust vectoring nozzle concept,AIAA,2006-3701[R].2006.
[4]Kenrick A Waithe,Karen A Deere.Experimental and computational investigation of multiple injection ports in a convergent-divergent nozzle for fluidic thrust vectoring,AIAA,2003-3802[R].2003.
[5]邓远灏,钟梓鹏,宋文艳.收敛-扩张喷管中运用次流推力矢量控制技术的计算研究[J].固体火箭技术,2004,28(1):29-32.
[6]乔渭阳,蔡元虎.基于次流喷射控制推力矢量喷管的试验及数值研究[J].航空动力学报,2001,16(3):273-278.
[7]吴雄,吴敏,张健,等.飞行参数对射流矢量喷管内流场影响的数值模拟[J].推进技术,2009,30(2):234-239.
[8]吴雄.固体发动机燃气二次喷射理论与试验研究[D].长沙:国防科学技术大学,2007.
[9]孙得川.二次射流干扰流场及其控制参数研究[D].西安:西北工业大学,2000.
[10]刘辉,邢玉明,额日其太.气体二次喷射矢量喷管三维流场计算[J].北京航空航天大学学报,2009,35(10):1174-1178.

