聚合物固体粒子在熔体中的流动和传热数值分析
梁 畅,罗 兵
(北京化工大学机电工程学院,北京100029)
聚合物固体粒子在熔体中的流动和传热数值分析
梁 畅,罗 兵
(北京化工大学机电工程学院,北京100029)
对螺杆挤出机螺槽建立了准三维的流动和传热模型,模拟了聚合物固体粒子在熔体中的流动、受热、温升和熔融行为;采用横纵向截面研究了聚合物固体粒子的速度和温度随时间的变化情况;通过计算得出了固体粒子熔融所需要的时间以及流场总能量增量中外部传热和内部黏性耗散生热所占的百分比。结果表明,机筒传热和黏性耗散对系统能量增加的贡献为3.68∶1。
聚合物;固体粒子;熔体;流动;传热;螺杆挤出机;数值分析
0 前言
聚合物的加工过程,是将聚合物的固体材料(粒料或粉料的形式)加入到加工设备中,经历流动、受热、相变、熔化、混合,最终以熔融的状态流出。螺杆挤出机和注塑机的熔融段是发生流动、传热和相变的主要区段,来自机筒上加热装置的传热和已熔融聚合物在流动中产生的黏性耗散生热成为聚合物固体粒子熔融的主要能量来源[1]。研究聚合物固体粒子在熔体中的流动和传热过程,有助于分析聚合物在螺杆挤出机流道中输运和相变的过程,也使描述熔融所需要的时间和经历的长度成为可能,从而使熔融段的设计更为准确。
研究实验中发现,啮合同向双螺杆熔融过程中,无论是粒料还是粉料,未熔融的固体是分散地悬浮在熔体当中的[2],即众所周知的“海-岛”熔融模型。袁明君等[3-5]把聚合物的加工过程本身视为对固体粒子进行操作处理的过程,通过实验观察了固体粒子在流动过程中的变形、取向和熔融问题,分别建立螺槽外层和内部的有熔体迁移和无熔体迁移的二维固体粒子熔融的模型。Chen等[6]探索了二维流场中,固体小粒子在熔体中剪切流场下的变形、破碎和熔融的变化历程和机理,得出了粒子完全熔融所需要的时间。
本文以一个悬浮在熔体中的固体粒子为研究对象,建立准三维流场,用有限元分析软件进行模拟计算,从空间坐标和时间等4个维度直观地反应其流动、受热以及熔融变化的过程,并研究该过程中的能量来源及其所占百分比。该模型既适用于模拟双螺杆挤出熔融过程中非啮合区螺槽内的“海-岛”模型熔融过程,也适用于研究单螺杆挤出熔融过程中螺槽内固体床破碎、悬浮在熔体中进行熔融的过程。
1 准三维流场固体粒子流动和传热模型
为了简化起见,将双头螺纹元件的一个螺槽(如图1所示)展开(如图2所示)。固体粒子位于X Y截面的中间处,沿流动方向,粒子位于流场长度的1/6处。螺杆及流场的几何参数如表1所示。
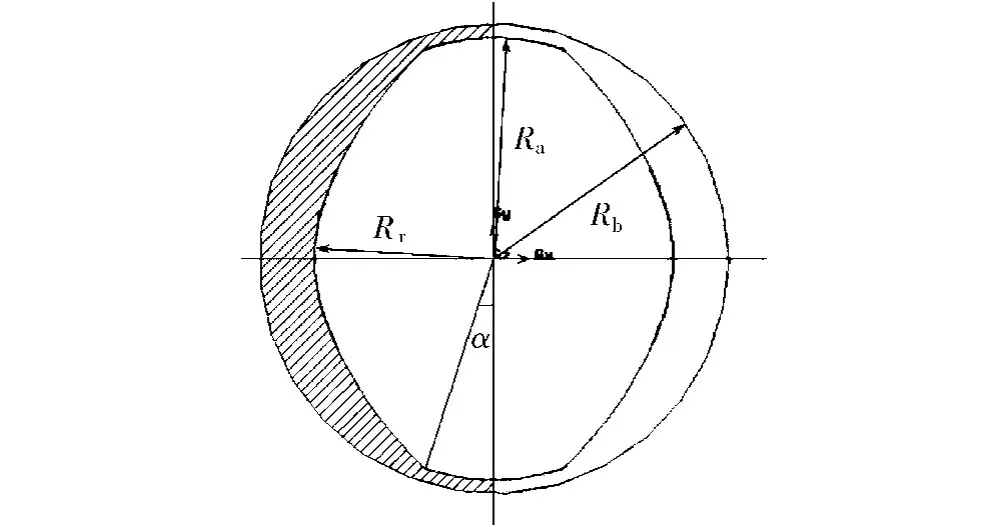
图1 螺槽示意图Fig.1 Schematic diagram of screw channel
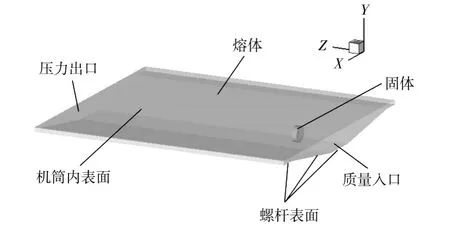
图2 螺槽流道展开及边界示意图Fig.2 Schematic diagram of unfolded screw channel and flow field boundaries

表1 流场的几何参数Tab.1 Geometries of flow field
考虑聚合物特性和挤出机加工特性,做如下基本假设和简化:(1)雷诺数较小,物料做层流流动;(2)熔体为不可压缩流体;(3)流道壁面无滑移;(4)忽略惯性力与体积力;(5)流场为开放流场,忽略压力降;(6)计算域内熔体为全充满状态。
假设螺杆不动,机筒以与挤出方向相反的方向运动,在螺槽内形成剪切流场。聚合物在熔融区的质量、动量和能量守恒方程如式 (1)~(3)[1]所示。
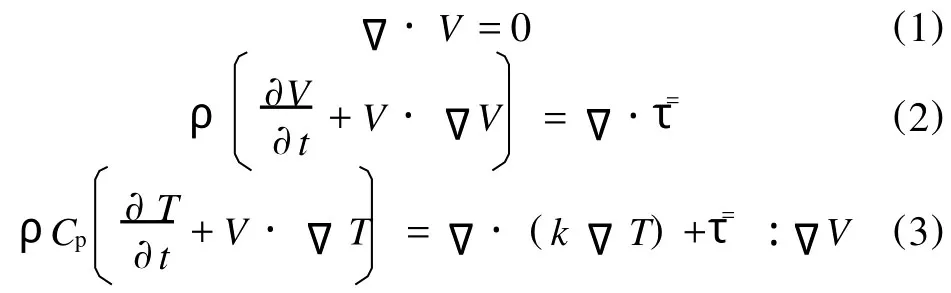
式中 ρ——物料相对密度,kg/m3
Cp——物料的定压比热容,J/(kg·K)
k——物料导热系数,W/(m·K)
T——温度 ,K
τ——剪切应力,N/m2
V—速度,m/s
式(3)等号右侧有2项,第一项为导热项,第二项是黏性耗散生热项,2项之和等于热传导和黏性耗散共同作用产生的系统能量增加。而式(4)是不计黏性耗散、仅仅考虑热传导而产生的系统能量增加的数学模型。本文将分别应用式(3)和式(4)来考虑系统的能量增加来比较热传导和黏性耗散对能量增加的贡献。
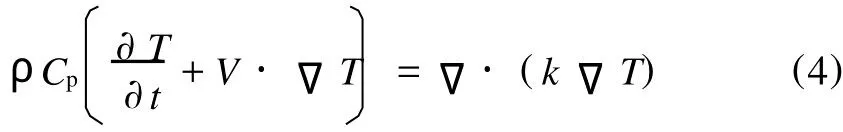
2 数值计算结果与分析
模拟计算采用的物料为齐鲁石化公司生产的牌号为HDPE-1158的高密度聚乙烯(PE-HD),其物性参数如表2所示。比热采用实际测量值,与物料温度成线性关系。

表2 HDPE-1158的物性参数Tab.2 Material properties of HDPE-1158
聚合物流体为幂律流体,本构方程为如式(5)所示,采用 HDPE-1158的物性参数计算相关变量。

式中 μ——黏度,Pa·s
m——稠度,Pa·s
入口端面为质量流率入口,出口端面为压力出口,机筒表面输入恒定的热流密度,且以与螺杆相反的速度沿X Z平面移动。螺杆表面静止且为绝热表面(如图2和表3所示)。控制方程与边界条件和初始条件一起构成聚合物固体颗粒流动与熔融的非稳态传热问题。应用FLUEN T有限元分析软件,基于有限控制容积法对定解问题进行离散化,运用 SIMPLEC算法,对非稳态传热问题进行求解。

表3 流场计算的边界条件和初始条件Tab.3 Boundary conditions and initial conditions
2.1 熔融过程中残留固体的形态随时间的变化情况
有限元计算结果显示,随着流动和传热的进行,固体粒子温度升高并逐渐破碎、熔化,如图3所示。为了突出固体粒子的熔融过程,显示残留固体粒子的位置和形态,图3中对熔体进行隐藏处理,即计算域内的空白处为熔体。在0.01~0.03 s的时间范围内,固体颗粒的温度明显升高,在剪切作用下,粒子变形,且表面层有破碎;在0.05~0.18 s的时间内,固体粒子的厚度迅速减小,粒子破碎成多个小颗粒,漂浮在熔体当中,熔化速率大大提高,同时在X向和Z向都发生了明显的位移;最终在0.2 s时,残留的固体粒度更小或者接近完全熔化。
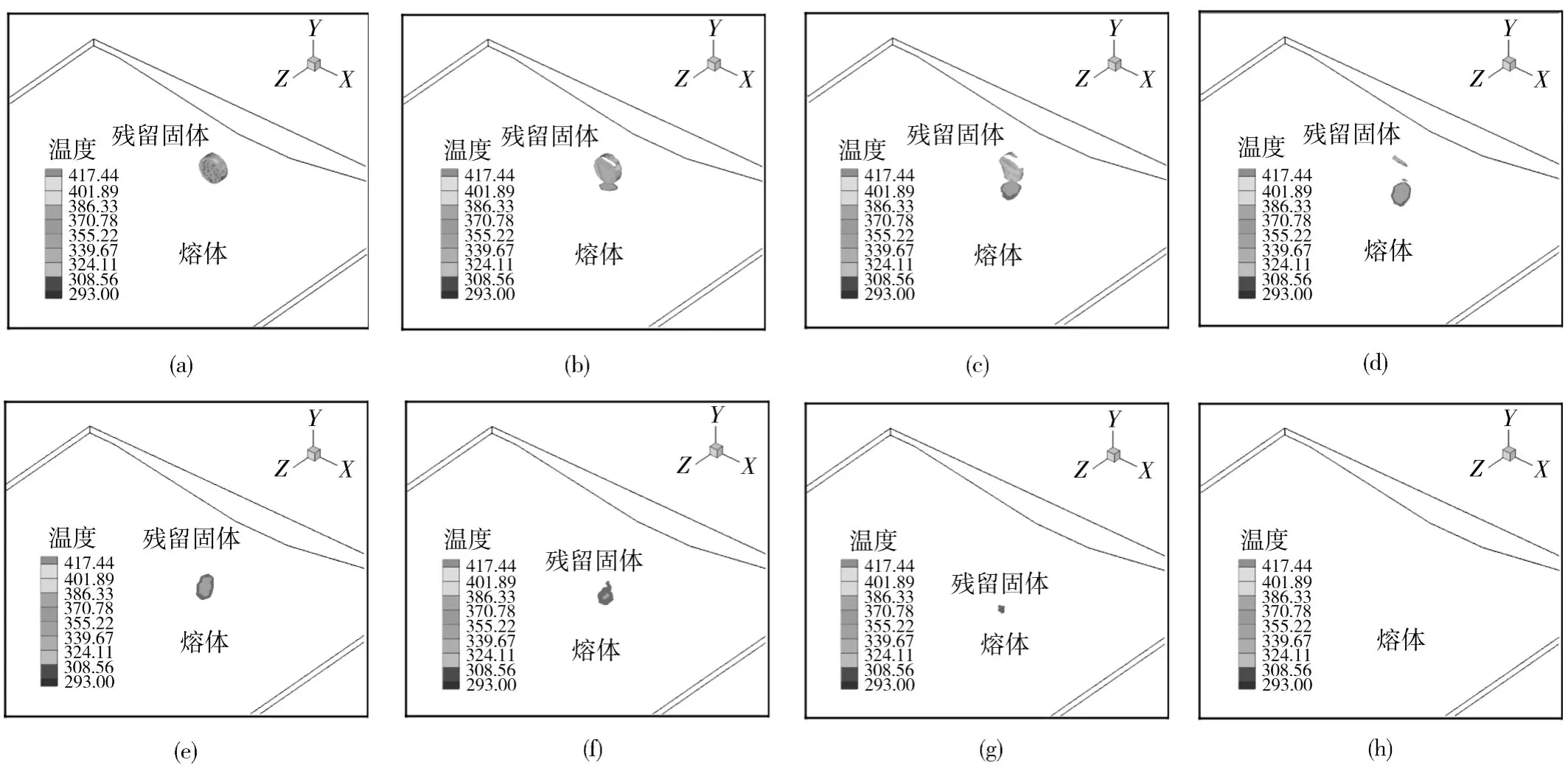
图3 残留固体的形态变化图Fig.3 Residual solid pellet under different times
为了详细地描述固体粒子在熔融流体中的流动和熔融状况,选取了2个截面来观察场量变化。一是沿着挤出方向即Z方向且通过固体粒子质心的纵向截面,另一个是垂直于Z方向的,并且通过固体粒子Z向质心的横向截面,如图4所示。随着固体粒子的流动、质心的移动,这个截面不断沿着坐标轴平行移动。
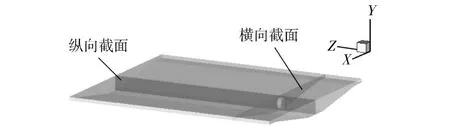
图4 横向截面和纵向截面示意图Fig.4 Schematic diagram of latitudinal and longitudinal sections
2.2 流场中固体粒子的流动状态随时间的变化
固体颗粒的流动过程直接影响熔融所需长度和传热过程。所以有必要描述固体粒子在流场中的流动形态,如图5所示。可以看到在流动的初始阶段(t=0.01~0.03 s),固体粒子的速度明显小于熔体的流动速度,在接近机筒内壁,还出现了受机筒拖曳而产生的反向流动。固液2相流动方向和流动速度的差异会产生熔体移走现象以及热熔体与冷固体之间的对流换热现象发生。随着时间的推移(t=0.04~0.1 s),固体粒子温度升高、发生熔化破碎,速度也不断增加,固体与熔体的温度差异逐渐减小,由于固体粒子的软化变形,使得固体区域的速度梯度较大,矢量密度较大,此时对流换热量减小,黏性耗散生热增多。直到最后接近熔融时(t=0.14 s),固体几乎完全熔融成熔体,速度矢量与熔体完全相同。
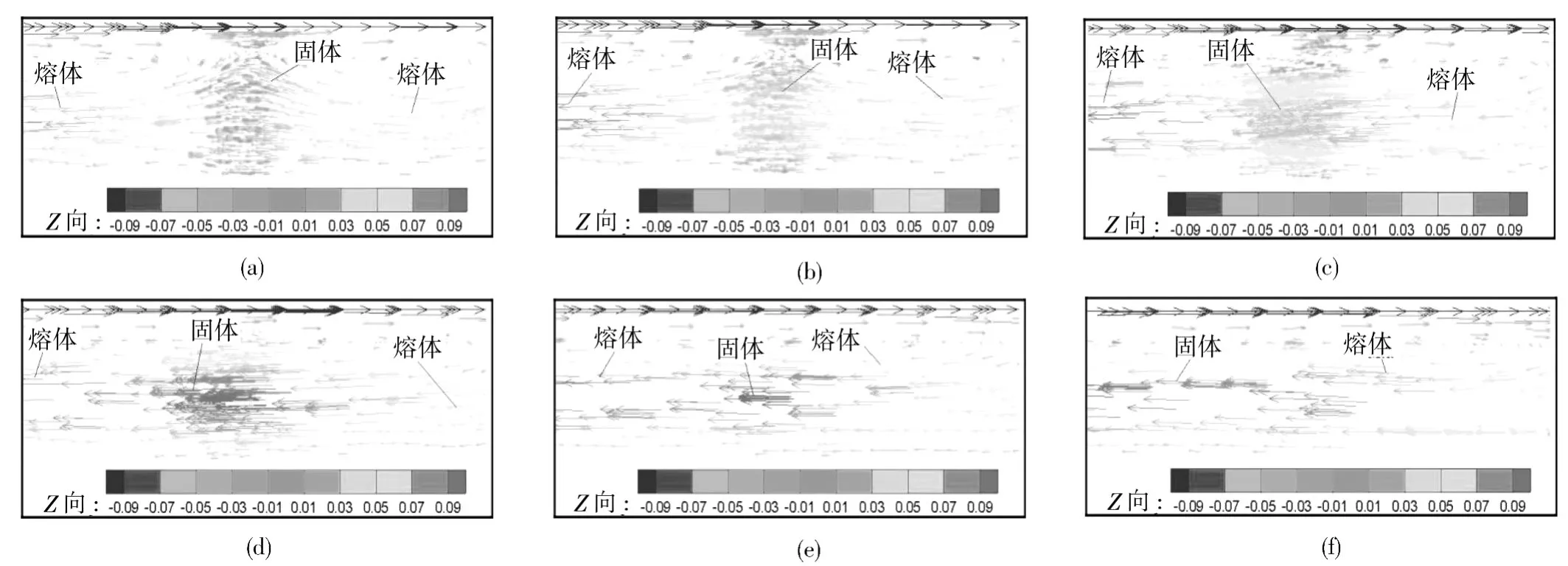
图5 纵向截面内的固体粒子区的速度矢量局部放大图Fig.5 Enlarged velocity vector of solid pellet in longitudinal sections
在横向截面的各个时间内除了发现固体粒子流动速度与固体粒子的熔融之间的关系之外,还能够明显地看到熔体在螺槽内的环形流动,如图6所示。
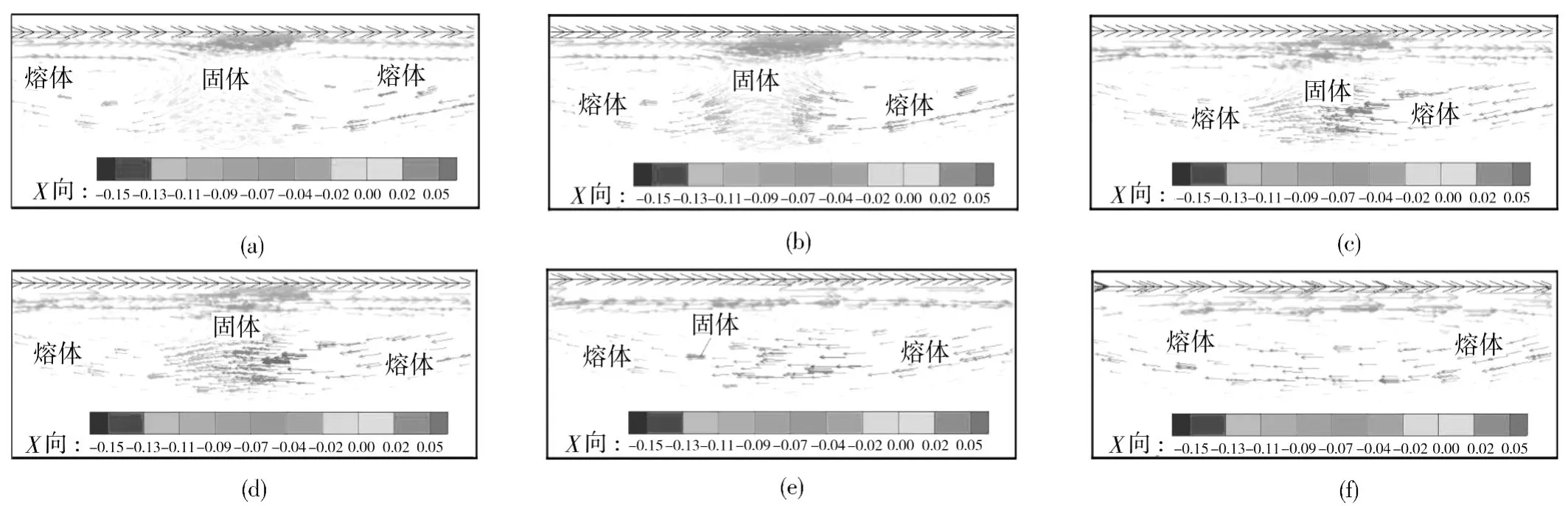
图6 横向截面内固体粒子区的速度矢量局部放大图Fig.6 Enlarged velocity vector of solid pellet in latitudinal sections
2.3 流场中固体粒子的熔融形态随时间的变化
图7展示了在纵向截面和横向截面不同时刻粒子的温度状态和熔融状态。从左侧的系列纵向截面可以看到,在流动之初(t=0.01~0.02 s),固体粒子靠近机筒内表面的部位在机筒反向拖曳作用下(见机筒运动方向),粒子上缘有向挤出反方向运动的趋势。但在熔体流的推动下,粒子出现了中部向挤出方向突出,上下缘受机筒内表面和螺杆表面的拖曳作用而产生的运动较缓现象,即出现弯月形的状态(t=0.03~0.06 s)。随着流动的进行,固体粒子的内部温度也逐渐升高,粒子中部向前的流动趋势最为明显,上下缘略滞后,粒子形态逐渐由弯月形逐步变成了不规则形状,同时粒子体积不断减小(t=0.08~0.2 s)。
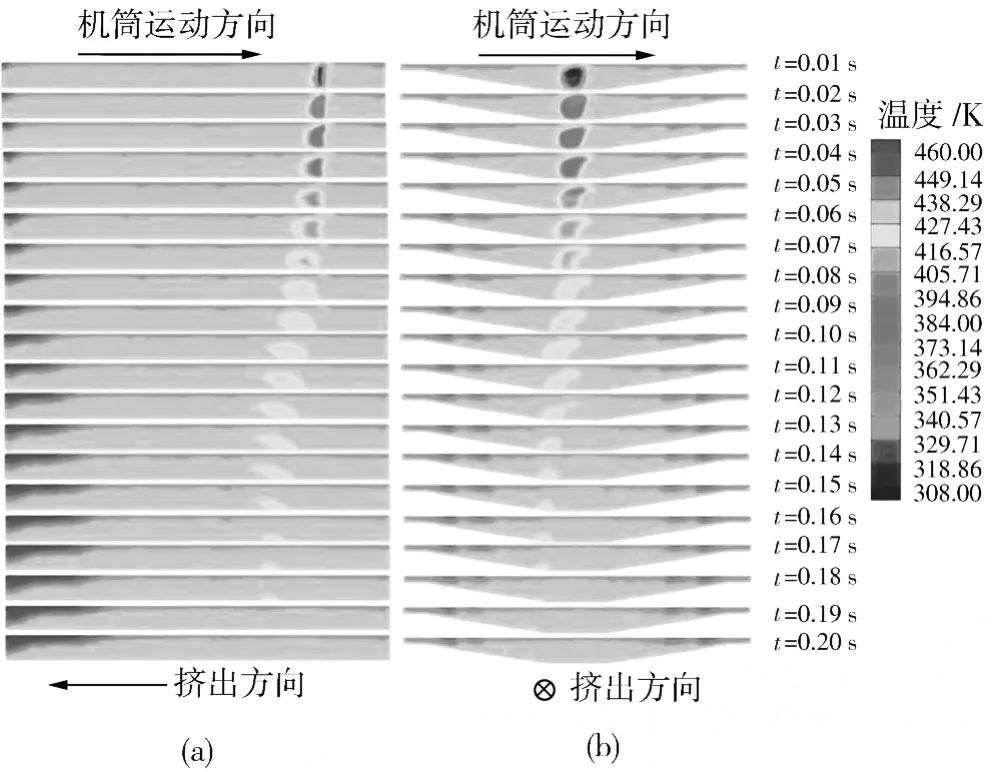
图7 固体粒子在 X向截面和Z向截面中的温度云图Fig.7 Temperature contours on sections of X-direction andZ-direction
从右侧的横向截面温度变化系列云图中可以看到,在流动之初(t=0.01~0.02 s),固体粒子的上缘在机筒传热作用下首先超过固化温度,粒子开始软化,并且在机筒表面的拖曳作用下,软化部分发生变形,形成倒置的逗号形状,同时粒子内部和芯部温度逐渐上升。随着时间的推移,粒子的熔融从上缘逐渐过渡到粒子中部,而靠近螺槽底部的残余粒子最后完成熔融。
2.4 固体粒子熔融所需要的时间和长度
图8为固体区和熔体区的温度极值变化曲线,对于本文,固体区和熔体区的最低温度值更有研究意义。固体区的最低温度从293 K开始,逐步升高。熔体区的最低温度则经历先降低、后升高的趋势,这是由于熔融开始后,固体粒子向前流动并进入熔体区,使得在熔体区域内也有低温的固体,即熔体区的最低温度是进入熔体区的固体粒子所携带的最低温度。随着机筒的持续加温、熔融的持续进行,熔体区的固体粒子得到熔化、温度升高,由于粒子可能没有完全离开固体区,所以固体区的最低温度也是需要关注的指标。从图8中可以看到,固体区的最低温度也在不断上升,这可能由于固体粒子的离开,熔体填补到固体粒子原来所占的区域,所以会出现固体区最低温度(可能是熔体的温度)高于熔体区的最低温度(固体粒子的最低温度)。2条曲线能够完全展示整个流场中的固体粒子的最低温度,无论此时固体粒子在哪一个区域。当这个最低温度超过熔融温度420.8 K,说明熔融过程结束。可以看到,在0.2 s时,熔体区的最低温度超过聚合物材料的熔融温度,所有残留固体熔融成熔体,固体粒子完成熔融。此时,固体粒子的Z向位移为7 mm。
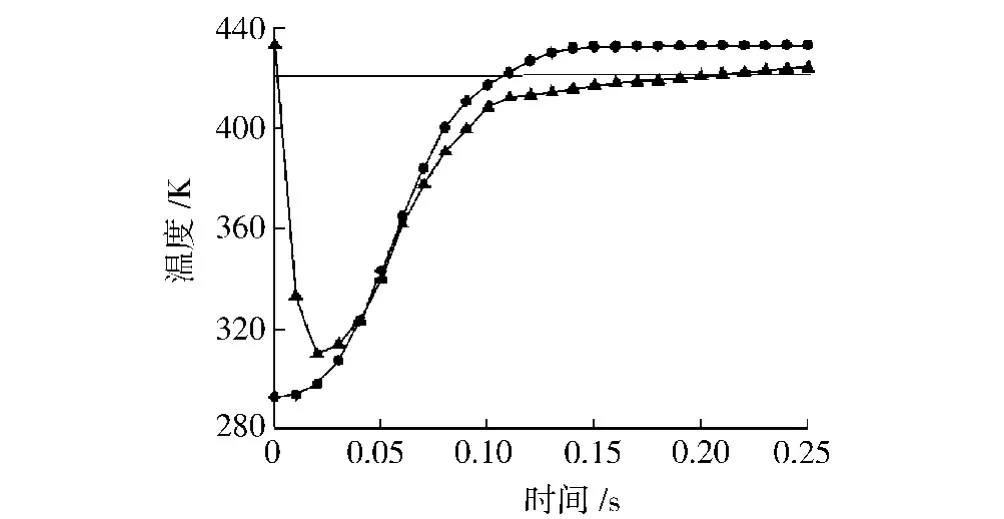
图8 固体区和熔体区的温度极值曲线Fig.8 Extreme temperature in solid and liquid zone
2.5 导致流场热力学能增加的能量输入
流场初始有高温的熔体,也有室温的固体粒子,随着流动和传热的进行,熔体的温度升高,固体粒子温度升高、熔融成熔体,并和熔体一起继续升温,由熔体和固体粒子组成的系统热力学能增加。能量来源于2个部分:一是源于机筒壁上外加热源的热传递,二是源于聚合物流动时产生的黏性耗散。本文通过考虑黏性耗散生热[式(3)]和不考虑黏性耗散生热[式(4)]来计算黏性耗散对于流场热力学能增加的贡献(其他条件完全相同)。从流动开始到熔融完全结束(0.2 s),考虑黏性耗散生热时,流场中总热力学能增量是59.0 J,如果不考虑黏性耗散生热,流场中的总热力学能增量是46.4 J,两者差值12.6 J为黏性耗散导致的热力学能增量,而不计黏性耗散生热的热力学能增量46.4 J则来源于机筒加热的能量输入。所以机筒传热和黏性耗散对于系统能量增加的贡献为3.68∶1,即系统热力学能的增加当中,78.6%来源于机筒加热,21.4%来源于黏性耗散生热。
3 结论
(1)固体粒子在熔融过程中伴随明显的流动和变形行为,流动和变形促进了熔融的进行;熔融最早发生在机筒内壁附近区域,并逐渐扩散到粒子芯部,靠近螺槽根部的残余粒子最后完成熔融;
(2)对于本文所研究的算例,一个悬浮在高温熔体中的室温固体粒子达到熔融温度需要的时间和轴向距离可以较为精确地量化;
(3)由熔体和固体粒子所组成的系统热力学能的增加当中,约3/4来源于机筒加热,1/4来源于黏性耗散生热。
[1] 任冬云.双螺杆挤出的非充满熔融理论的研究[D].北京:北京化工大学机电工程学院,1997.
[2] 朱林杰.啮合同向双螺杆挤出过程聚合物熔融机理研究[D].北京:北京化工大学机电工程学院,1999.
[3] 袁明君,朱复华.单螺杆挤出过程中固体粒子的变形、取向与熔融Ⅰ[J].中国塑料,1999,13(11):88-94.
[4] 袁明君,朱复华.单螺杆挤出过程中固体粒子的变形、取向与熔融Ⅱ[J].中国塑料,1999,13(12):80-83.
[5] 袁明君,朱复华.单螺杆挤出过程中固体粒子的变形、取向与熔融Ⅲ[J].中国塑料,2000,14(1):93-100.
[6] Chen H B,Sundararaj U,Nandakumar K.Modeling of Polymer Melting,Drop Deformation,and Breakup Under Shear Flow[J].Polymer Engineering and Science,2004,44(7):1258-1266.
Numerical Analysis of Flowand Heat Transfer of a Polymer Solid Pellet in Melt
LIAN G Chang,LUO Bing
(School of Mechanical and Electrical Engineering,Beijing University of Chemical Technology,Beijing 100029,China)
A quasi-3-dimension flow and heat transfer model for extruder screw channel was established to investigate the flow,heating,and melting behavior of solid particles in a polymer melt.Sections along longitudinal and latitudinal directions were selected to study the velocity and temperature of solid pellet as functions of time.The time required for the solid particles to melt and the internal energy increase were calculated accurately.It was found that the ratio of transferred heat and internal energy was 3.68∶1.
polymer;solid pellet;melt;flow;heat transfer;screw extruder;simulation analysis
TQ320.5+2
B
1001-9278(2011)06-0097-05
2011-02-22
联系人,liangchang@mail.buct.edu.cn

