一类非局部退化反应扩散方程组解的存在性

崔国忠， 郭从洲， 荆焕先， 魏保军

(信息工程大学 理学院 河南 郑州 450001)

一类非局部退化反应扩散方程组解的存在性

崔国忠， 郭从洲， 荆焕先， 魏保军

(信息工程大学 理学院 河南 郑州 450001)

讨论了一类退化的具有非局部项的非线性反应扩散方程组解的存在性.首先利用了正则化方法证明正则问题解的存在性，进而证明了非线性反应扩散方程组的古典解的存在性；其次利用上下解方法来解决非线性反应扩散方程组解的整体存在，针对参数所满足的条件不同来构造不同结构的上解，从而得到了方程组解的整体存在条件.

古典解； 正则化； 上解； 整体存在性

0 引言

考虑如下非局部退化反应扩散方程组的初边值问题：

(1)

其中,Ω⊂RN为有界域，具有光滑边界∂Ω，参数满足min{m,n}>1，α>0,β>0,p>0,q>0,初值u0(x)和v0(x)是非负连续函数.

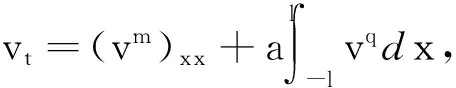
1 古典解的存在性

(2)

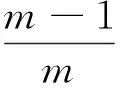
(3)

假设初值u0,v0满足:

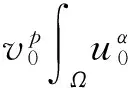
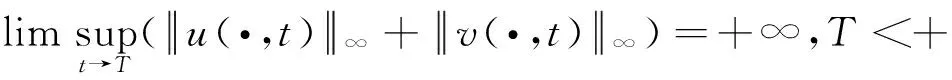
证明由于在边界u=v=0并且min{m,n}>1，因此系统不是一致抛物的，标准的抛物理论不能直接使用.考虑如下的正则化问题:

(4)

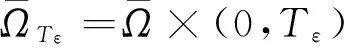
以λ>0表示-Δ在区域Ω上的第一特征值，即

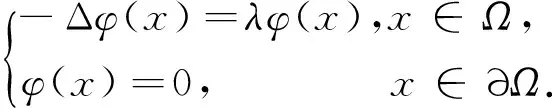
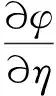
考虑常微分方程的定解问题:

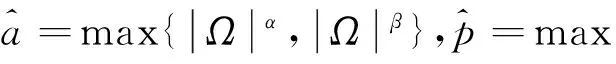
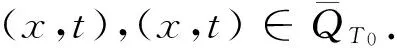
证明令w=uε-φ(x,t)，通过计算可得

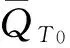
证明设Uε=uεt，Vε=vεt,直接计算可得

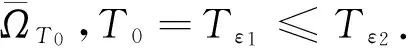
证明设W=uε1-uε2，Z=vε1-vε2，由引理3有uε2t,vε2t≥0，并记

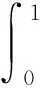
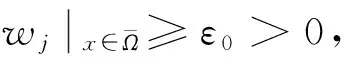
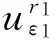
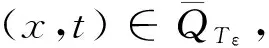
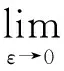
(5)

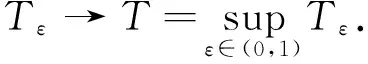
因此，可以得出(5)式即为方程组(3)的古典解，定理1得证，并且引理3表明有如下结论成立.

定理2假设条件(H1)～(H3)成立，则方程组(3)的解(u,v)满足在QT的任何紧子集上都有ut≥0,vt≥0.

2 整体解的存在性

对具非局部源的耦合退化模型(1)，在定理1的基础上，利用上下解方法，通过构造不同特殊结构的有界上解，给出系统解的整体存在条件.

定理31)如果m>α,n>β,pq<(m-α)(n-β)时，则对任何区域和任何初值，问题(1)的解都整体存在.

2)当m>α,n>β，pq=(m-α)(n-β)，pq>αβ时，若Ω至少在一个方向薄时，则问题(1)的解整体存在.

3)如果m<α,n<β，pq<(m-α)(n-β)时，若初值u0(x),v0(x)中有一个充分小，则问题(1)的解整体存在.

4)当m<α+p,n<β+q时，对充分小的初值u0(x),v0(x)，问题(1)的解整体存在.

证明定理3前，先给出2个引理.

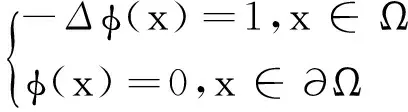
证明参见文献[7-8]中引理1.

引理6假设存在a>0,b>0,δ>0，使得

(6)

则问题(1)的解整体存在.

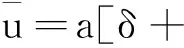
定理3的证明任取Ω′，使得Ω⊂⊂Ω′，φ为Ω上特征问题的解.令

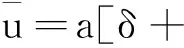
由引理6，要证明定理3，只需证明存在正常数a>0,b>0,δ>0使(6)成立.

显然，如果存在a>0,b>0,δ>0，使得

(7)

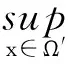
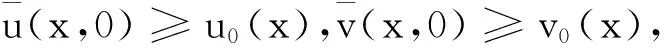
定理41)当1+p>β,1+q>α且(1-α)(1-β)>pq时，问题(1)的解整体存在.

2)当(1-α)(1-β)=pq,1>α,1>β时，问题(1)的解整体存在.

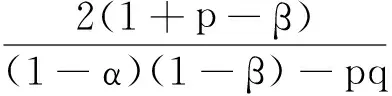
则取C>0充分大,使得

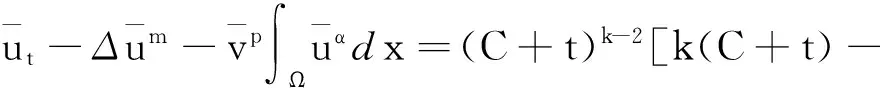
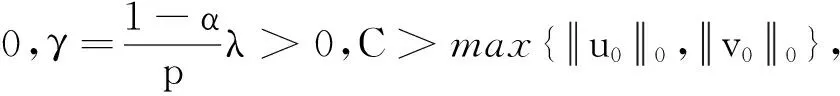
[1] Galaktionov V A,Kurdyumov S P,Samarski A A.A parabolic system of quasilinear equations (Ⅱ)[J].Differential Equations,1985,21: 1544-1559．

[2] Mu Chunlai,Su Ying．Global existence and blow-up for a quasilinear degenerate parabolic system in a cylinder[J]．Appl Math Lett,2001,14(6):715-723．

[3] 吴定平，李玉环，崔泽建.一类耦合退化抛物方程组在有机界域中的爆破[J]．四川大学学报:自然科学版,2005,42(2):229-233．

[4] Deng Weibing,Duan Zhiwei,Xie Chunhong．The blow-up rate for a degenerate parabolic equation with a non-local source[J]．Math Anal Appl,2001,264(2)：577-597．

[5] Duan Zhiwei,Deng Weibing,Xie Chunhong．Uniform blow-up profile for a degenerate parabolic system with non-local source [J]．Computers &Math Appl,2004,47(6/7):977-995．

[6] Deng Weibing,Li Yuxiang,Xie Chunhong．A nonlinear degenerate parabolic system with non-local source and crosswise-diffusion[J]．Z Angew Math Phys,2003,54(3):503-516．[7] Rossi J D,Wolanski N.Blow-up vs.global existence for a semilinear reaction-diffusion system in a bounded domain[J]．Comm Partial Diff Eq,1995,20(11):1991-2004．

[8] Yang Ming．Global existence and blow-up of a degenerate parabolic system[J]．Journal of Southeast University:English Edition,2003,19(4): 427-431．

ExistenceforaClassofDegenerateReaction-diffusionEquationswithNonlocalSource

CUI Guo-zhong, GUO Cong-zhou, JING Huan-xian, WEI Bao-jun

(InstituteofScience,InformationEngineeringUniversity,Zhengzhou450001,China)

The existence for a class of degenerate nonlinear reaction-diffusion equations with nonlocal source was investigated. Firstly,the existence of the solution of the regularization equations with the regularization method,and the existence of classical solution of the reaction-diffusion equations were proved.Secondly,by making use of super and low solution method,the global existence for the nonlinear reaction-diffusion equations was solved. Following the conditions for the parameter to construct different structures of the super solutions of the equations,the global existence conditions of the solutions of the equations were obtained.

classical solution； regularization； super solution； global existence

O 175.26

A

1671-6841(2011)04-0005-05

2011-03-30

崔国忠(1966-)，男，教授，博士，主要从事偏微分方程研究，E-mail:cuigzh1966@163.com；通讯作者：荆焕先(1985-)，男，硕士研究生，主要从事偏微分方程研究，E-mail:tiger785@163.com．