一种时间自动机时钟离散化算法

朱维军，周清雷

(郑州大学 信息工程学院 河南 郑州 450052)

一种时间自动机时钟离散化算法

朱维军，周清雷

(郑州大学 信息工程学院 河南 郑州 450052)

稠密时间自动机被广泛应用于实时系统自动验证.然而其在补操作下不封闭，因而导致多种线性实时性质不可验证.离散时间自动机虽不存在此问题，但该模型表达能力偏弱.因此，提出了一种时间自动机时钟离散化算法，结合时钟物理约束因素，证明了新方法可有效解决上述问题.

时间自动机； 模型检测； 物理时钟； 离散化

0 引言

模型检测的形式化理论、计算模型与验证算法是近年来计算机科学的研究热点之一.基于模型检测算法的验证工具已经在硬件设计、网络协议、网络安全协议、实时系统、软件规范等领域取得了广泛应用.在实时计算系统模型检测中，时间自动机[1]已成为建立模型的事实标准，各种实时逻辑[2-7]则被提出并用来描述系统需满足的性质.然而，在实数时间域上取值的线性实时逻辑与时间自动机通常是不可模型检测的.解决的方法有：对线性实时逻辑的语法做某种约束[2，4]；约束时钟语义到离散域[8].现有的研究从数学层面上证明了离散时间自动机的模型描述能力低于稠密时间自动机[4,9]，继而导致了寻找既能保持稠密时间自动机的描述能力(特别是描述异步时钟能力)，同时又能保持离散时间自动机由于补操作封闭因而正则实时性质完全可模型检测能力的途径[9-13].对此问题，我们的研究从实用角度揭示了一些有益的结论.

1 时间自动机

定义1对时钟集合x，时钟约束集合Φ(X)={δ|δ=xc|x≤c|x≥c|δ1∧δ2}，其中δ1,δ2是时钟约束且x∈X,c∈Q.

定义2对τ∈R+,v表示时钟赋值，对任意x∈X,v(x)+τ表示对时钟x，时钟流逝τ后的时钟赋值.对Y⊆X,[Y→0]v表示对任意x,x∈Y,v(x)∶=0;对任意x,x∉Y,x∈X,v(x)不变.

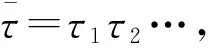
2)进展性：对任意t∈R+，存在i≥1使得τi>t，

是时间序列.

定义4时间转换表是一个五元组(Σ,S,S0,X,E).其中，Σ是有限输入字母表.S是有限状态集.S0⊆S是开始状态集，X是有限时钟集.E⊆S×S×Σ×2X×Φ(X)是转换规则集.一条转换规则具有形式(s,s′，a,λ,δ)，表示对输入字母a，如果满足时钟约束δ，那么从状态s转换到状态s′，并对任意x∈λ,v(x)∶=0.

定义6时间自动机是一个六元组A=(Σ,S,S0,X,E,F)，其中,(Σ,S,S0,X,E)是一个时间转换表,F⊆S是接受状态集.

2 基于真实物理时钟的时间自动机表达能力

我们注意到，时间自动机作为实时计算模型，它被广泛应用于工程实时系统的形式化验证.在任何这样的实际系统中，所有的时钟都需要满足它的物理规律.任何真实的物理时钟都不可能像数学时钟一样以无穷小的逼近步长来计时，必然存在足够小的纯小数Δ，使得所有物理时钟的最小计时单元都大于等于Δ.当这样的Δ取最大值Δmax时，我们就可以得到一个以Δmax为时间单元的时钟(集)，使得以它(们)为时钟(集)的离散时间自动机TAN足以描述稠密时间自动机TAΔ所能描述的真实实时系统.定理1证明了这一点.

定理1TAN与TAΔ等价

证明1)令TAΔ时间域为TIME，它的时间单元为足够小的有理数Δ，做映射f：TIME→N，令1N=m·1TIME，m∈N，其中1N=1表示时间域N中的一个单元，1TIME=Δ∈Q,∃k,Δ=1/k表示时间域TIME中的一个时间单元.令m=k，则m·1TIME=m·Δ=k·1/k=1=1N，因此，k·TIME=N，即通过乘系数k，TA在TIME上的解释转化为在N上的解释.

2)同理可证TA在N上的解释可通过乘系数1/k转化为在TIME上的解释.

3 离散时间自动机构造算法

Procedure construct_TAN

Input:TAΔ=(Σ,S,S0,X,E); Output:TAN=(Σ′,S′,S0′,X′,E′)

Begin

G∶=φ;

For allδ=x#c∈Φ(X) //#∈{<,=,>,≤,≥}

c′∶=c/Δ; //时钟约束所有常量映射为正整数(显然为正整数，证明略)

G∶=G∪{c′};

End for

m∶=mcd(G); //求G中元素的最大公约数

Σ′∶=Σ;S′∶=S;S0′∶=S0;X′∶=X;//构造离散时间自动机字母表状态集时钟集

E′∶=φ; //离散时间自动机转换规则集初始化

For alle=(s×s′×a×λ×δ)∈E

δ′∶=con(δ) //调用自定义函数求最优化时钟约束

e′=s×s′×a×λ×δ′;E′∶=E′∪{e′} //构造转换规则集

End for

End begin //离散时间自动机构造完成

Function con(δ) //定义函数，求离散时间自动机时钟步长最优化

For allx#cinδ

c′∶=c/Δ;c″∶=c′/m,replace(x#c″,x#c,δ) //所有约束被最优化之后的约束所替换

End for

returnδ//返回最优化之后的时钟约束集

End function

定理2算法1的时间复杂度为O(n)

证明对TAΔ中转换规则集E，构造TAN转换规则E′需时间O(|E|)；构造TAN的输入字母集需时O(|Σ|)；构造TAN状态集需时O(|S|+|S0|)，构造TAN时钟集需时O(|X|)；而求时钟约束集正整数常量的最大公约数需时O(|Φ(X)|)，因此算法时间复杂度为O(|E|+|Σ|+|S|+|S0|+|X|+|Φ(X)|)，而输入时间自动机TAΔ的长度n=|E|+|Σ|+|S|+|S0|+|X|+|Φ(X)|，因此算法1为线性时间算法.

定理1保证算法1的有效性与正确性，定理2则证明了算法具很高的效率.

定理3[9]离散时间自动机TAN可模型检测.

4 结论

算法1的优势在于可以验证真实物理世界中实时计算系统的各种实时性质(包含安全性与可靠性)，并可以开发工具进行全自动验证，而且无需受到现有各种方法的约束.新方法仅仅损失了数学理论上的时间自动机验证能力，而对真实物理世界中实时计算系统的自动机模型表达能力并无降低，换来的是对所有时间正则性质的可(自动)验证能力(定理3)，这是现有方法所不具备的.

由于时间自动机已被应用于航天控制软硬件计算系统、实时通信网络等领域的实时计算模型检测，因此，新算法有着良好应用前景，我们下一步准备在新算法基础上开发工具.

[1] Alur R, Dill D L. A theory of timed automata[J].Theoretical Computer Science, 1994, 126(2): 183-235.

[2] Alur R, Feder T, Henzinger T A. The benefits of relaxing punctuality[J].Journal of the ACM, 1996, 43(1): 116-146.

[3] Alur R, Henzinger T A. A really temporal logic[J]. Journal of the ACM, 1994, 41(1): 181-204.

[4] Alur R, Henzinger T A. Logics and models of real time: A survey[C]//Proceedings of the Real-Time: Theory in Practice, REX Workshop, LNCS600.Berlin, 1992: 74-106.

[5] Duan Zhenhua. Modeling of hybrid systems[M]. Beijing: Science Press, 2004: 1-43.

[6] Zhou C, Hoare C A, Ravn A P. A calculus of duration[J]. Information Processing Letters, 1991, 40(5): 269-276.

[7] Li Guangyuan, Tang Zhisong. Translating a continuous-time temporal logic into timed automata[C]// Proceedings of the First Asian Symposium on Programming Languages and Systems (APLAS 2003), LNCS2895. Berlin, 2003: 322-338.

[8] 朱维军, 张海宾, 周清雷. 离散时间区间时序逻辑可满足性的判定[J]. 电子学报，2010，38(5)：1039-1045.

[9] Wilke T. Specifying timed state sequences in powerful decidable logics and timed automata[C]//Proceedings of the Third International Symposium on Formal Techniques in Real-Time and Fault-Tolerant Systems, LNCS863. Berlin, 1994：694-715.

[10] 晏荣杰,李广元,徐雨波,等. 有限精度时间自动机的可达性检测[J]. 软件学报,2006,17(1): 1-10.

[11] Hanson M R. Model-checking discrete duration calculus[J]. Formal Aspects of Computing, 1994, 6A: 826-845.

[12] 姚兴华，邓培民，易忠.弱可逆有限自动机分解的一个结果[J]. 广西师范大学学报：自然科学版，2008，52(1)：31-33.

[13] 宋煌, 郑丽萍, 庄雷, 等. 时间自动机与自动验证[J]. 郑州大学学报：理学版，2001，33(2)：30-34.

NovelAlgorithmforDiscretizationofClocksofTimedAutomata

ZHU Wei-jun, ZHOU Qing-lei

(SchoolofInformationEngineering,ZhengzhouUniversity,Zhengzhou450052,China)

Some linear real-time properties can not be verified automatically because dense timed automata are not closed under complement operation. Discrete timed automata can be used to model checking discrete regular properties, but the express power of them is weak. A novel procedure was given to construct discrete timed automata from their dense time version. For physical factors of clock constrain, the new algorithm was used to solve the problem above efficiently.

timed automata; model checking; physical clocks; discretization

TP 301

A

1671-6841(2011)03-0070-03

2010-06-03

国家(863)高技术研究发展计划项目，编号2007AA010408；国家自然科学基金青年基金资助项目，编号61003079，60901078；河南省重大科技攻关计划项目，编号092101210104.

朱维军(1976-)，男，讲师，博士，主要从事计算机形式化方法、高可信软件、实时计算等研究，E-mail:zhuweijun76@163.com.