单车型动态车队调度问题的时空分解模型构造

李 冰

(郑州大学 管理工程系 河南 郑州 450001)

单车型动态车队调度问题的时空分解模型构造

李 冰

(郑州大学 管理工程系 河南 郑州 450001)

构造了问题的动态规划模型，详细地研究了模型中总收益函数的凹函数特性，进而设计线性逼近函数，构造问题的时空分解模型，从而达到将问题时空分解为多个单时段单节点问题的目的.

动态车队调度； 收益函数； 时空分解

0 引言

单车型动态车队调度问题描述[1-3]如下：服务周期T被等分为H个时段，运输网络中各节点处分别在这H个时段产生新的运输任务l，任务l的产生地i，目的地j和服务时间窗均为已知，如果任务l在其时间窗内没有被分配到车辆，则该任务自动消失；现有Q辆同一型号的货运车辆，且这Q辆车在服务周期开始时在各节点处的分配情况已知.现在要分别制定服务周期内各时段t各节点i处的车队调度方案，使得整个服务周期内所能创造的总收益最大.

1 问题模型的动态规划形式

对问题的线性规划模型进行改进，将其表述成动态规划形式P1[1]

(1)

其中,xt表示服务周期内时段t各节点处采取载货移动形式的任务量；yt表示服务周期内时段t各节点处采取空车移动和原地驻留形式的车辆数量；Vt表示服务周期内时段t各节点处的可调配车辆数量；Lt表示服务周期内时段t各节点处可以发送的任务集合量；rlt表示车辆在时段t发送运输任务l所能创造的纯利润；cij表示车辆从节点i空移到节点j的成本；xlt为0-1变量，如果时段t运输任务l分配到一辆车则xlt=1，否则xlt=0；yijt表示时段t从节点i发往节点j的空车数.

因为模型的目标函数Ft(Vt,Lt)表示服务周期内时段t及t以后各时段的车队调度方案(xt,yt)所创造的总收益值，故又将目标函数称为总收益函数[1-4].

2 总收益函数分析

2.1单时段单节点收益函数分析

2.1.1单时段单节点总收益函数Fit(Vit,Lit)的定义[1]

Fit(Vit,Lit)表示时段t节点i处的车队调度方案(xlt,yit)所能创造的总收益值.因为(i,t)处的车队调度方案(xlt,yit)会对时段t以后各时段的车队调度方案制定产生影响，所以Fit(Vit,Lit)不仅包括车队调度方案(xlt,yit)在时段t所创造的收益，而且包括其对以后各时段的影响.故Fit(Vit,Lit)≠fit(Vit,Lit).

2.1.2Fit(Vit,Lit)的函数值确定方法

根据(i,t)处的运输需求量Lit，对车辆Vit进行合理调配，从而得到该处的车队调度方案(xlt,yit)，代入函数Fit(Vit,Lit)可求得收益值.由此可以看出，车辆供给量变量Vit直接影响着函数Fit(Vit,Lit)的取值，所以可以将函数Fit(Vit,Lit)看作车辆供给量变量Vit的函数，故又将其简记为Fit(Vit).

2.1.3单时段单节点车辆选择项排序

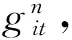
2.1.4单时段单节点车队调度

(2)

这里称ξit(Vit)为Fit(Vit)在Vit处的边际收益，由式(2)可以看出ξit(Vit)等于第Vit+1辆车所创造的总收益值.将函数Fit(Vit)在Vit处的斜率记作αit(Vit)，因为(i,t)处车辆供给量Vit相对较大，故边际收益ξit(Vit)可用函数Fit(Vit)在Vit处的斜率αit(Vit)来近似表示，即

图1 (i,t)处的凹收益函数Fig.1 Concave recourse function in region i at time t

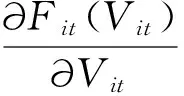
在图1中，αit(m)为总收益函数Fit(Vit)在m处的斜率，它可用来近似表示(i,t)处车辆供给量Vit为m时，增加一辆车所引起的总收益值改变量，即Fit(Vit)在m处的边际收益值ξit(m).

2.2选择项收益值分析

1)选择项为载货移动方式时的利润rlt或选择项为空车移动和原地驻留时的成本cij；

2)车辆到达目的地(j,t+1)后使得该处增加一辆车辆供给所带来的收益增加量ξj,t+1(Vj,t+1)，即(j,t+1)处的边际收益.

(3)

2.3单时段单节点车队调度方案确定过程的连锁关系

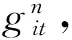
一旦时段t其他各节点发往目的地j的车辆数被确定就可以求得(j,t+1)处的车辆供给量Vj,t+1，从而利用(j,t+1)处的总收益函数Fj,t+1(Vj,t+1)求得αj,t+1(Vj,t+1)来近似边际收益ξj,t+1(vj,t+1)，该过程如图2所示.

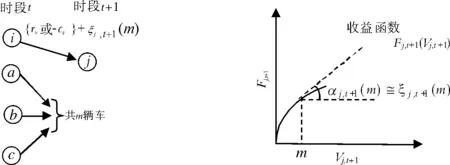
图2 边际收益值的求解Fig.2 Solution of marginal value in region i at time t

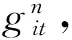
上述单时段单节点车队调度方案确定过程的连锁关系如图3所示.

图3 单时段单节点车队调度方案确定过程的连锁关系Fig.3 Process of solving fleet scheduling scheme to local problem for each terminal at each time period

由图3所示的关系图可以看出，要确定(i,t)处的车队调度方案，必须要确定时段t其他各节点处的车队调度方案，由此得知动态运输网络中各单时段单节点处车队调度方案的确定并不相互独立，而是通过目的节点在下一时段的车辆供给量相互之间发生着联系，从而使得问题很难分解为一个个相互独立的单时段单节点车队调度问题，大大增加了问题的求解难度.

2.4凹收益函数的线性逼近函数

凹收益函数是造成各单时段单节点处车队调度之间不相互独立的原因所在，也正是因为这种不独立性使得问题难于求解.

考虑将凹收益函数用线性函数来近似逼近，如图4所示.

图4 (j,t+1)处的线性收益函数Fig.4 Linear recourse function in region j at time t+1

由图4可以看出，当(j,t+1)处的凹收益函数被线性函数替代后，边际收益ξj,t+1(Vj,t+1)变为了常量，同该处的车辆供给量Vj,t+1无关，从而也无需确定时段t其他各节点发往目的地j的车辆数，故可直接将(j,t+1)处的边际收益记作ξj,t+1.

由此可知，当单时段单节点处的凹收益函数用线性函数替代后，问题被时空分解为了一个个相互独立的单时段单节点车队调度问题，从而使问题的求解得到了大大简化.线性逼近函数近似处理势必会对最终求出的解的精度产生一定影响，由于篇幅原因关于精度问题的分析作者将另撰文予以探讨.

3 时空分解模型的构造

3.1总收益函数的线性逼近函数设计

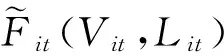
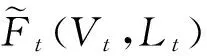
(4)

(5)

(6)

3.2约束条件的调整

问题的目标函数(即总收益函数)用式(6)形式的线性逼近函数替代之后可以分解为一个个单时段单节点的车队调度问题，从而使得求解过程得到大大简化.但当问题转化为单时段单节点车队调度问题之后，问题的约束也会随之发生变化，所以需要对原有的约束条件进行调整.对新形成的单时段单节点车队调度进行分析可以发现，载货车辆数被任务需求数所限定，但空移车数和原地驻留车数却缺少必要的限制条件[3,6].基于上述原因，引入一个新的控制变量uijt.

uijt：当i≠j时，表示时段t从节点i发往节点j的空车数上限；当i=j时，表示时段t在节点i原地驻留到时段t+1的车辆数上限，∀i,j∈N,t∈T.

从而为单时段单节点决策问题增加了一个新的约束条件

yijt≤uijt，∀i,j∈N,

(7)

3.3时空分解模型的构造

根据对目标函数和约束条件的调整，创建新的问题模型P2：

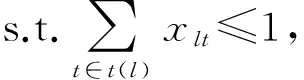
yijt≤uijt，∀i,j∈N,i≠j,

模型P2同P1相比其优越之处在于问题按时间和空间分解为了一个个单时段单节点的车队调度问题.

4 结束语

论文构造了问题的动态规划模型，详细分析了总收益函数的凹函数特性，进而设计出线性逼近函数，构造了问题的时空分解模型，从而将问题时空分解为一个个单时段单节点的车队调度问题.

[1] 李冰．单车型确定性动态车辆调配问题[J]．系统管理学报，2008，17(3)：353-360．

[2] 李冰，王化河．动态车队管理问题研究的现状与展望[J]．公路交通科技，2004，21(4)：109-113．

[3] 李冰．动态车队管理问题的模型及算法研究[D]．成都：西南交通大学，2003．

[4] 李冰．确定性动态车辆调配问题分析[J]．郑州大学学报：理学版，2006，38(2)：116-120．

[5] 李冰．随机动态车队管理问题研究[J]．系统工程，2005，23(1)：96-101．

[6] 李冰．多车型确定性动态车辆调配问题[J]．管理工程学报，2006，20(3)：52-56．

Spatial-TemporalDissolutionModelinDynamicFleetSchedulingProblemwithHomogeneousVehicleType

LI Bing

(DepartmentofManagementEngineering,ZhengzhouUniversity,Zhengzhou450001,China)

The dynamic programming model was expressed.Then the concavity of recourse function in the model was researched in detail.A particular linear function was devised to approximate the recourse functions.The spatial temporal dissolution model was formulated.The problem by time and space was decomposed into a series of local problems for each terminal at each time period.

dynamic fleet scheduling; recourse function; spatial temporal dissolution

U 492.312； F 540.82

A

1671-6841(2011)03-0078-05

2010-09-20

国家自然科学基金资助项目，编号71001091，71001090；河南省高等学校青年骨干教师计划项目，编号 教高〔2008〕708号；河南省教育厅自然科学研究计划项目，编号2009A120002.

李冰(1976-)，男，副教授，博士，主要从事运输组织优化、物流系统优化研究，E-mail:lbing@zzu.edu.cn．