相对序列空间的一个注记

王汉锋，李进金

(1.山东农业大学 数学系 山东 泰安 271018; 2.漳州师范学院 数学系 福建 漳州 363000)

相对序列空间的一个注记

王汉锋1，李进金2

(1.山东农业大学 数学系 山东 泰安 271018; 2.漳州师范学院 数学系 福建 漳州 363000)

回答了关于相对序列空间的一个公开问题,讨论了几种相对序列空间的部分关系及相对序列空间与Pytkeev空间、相对序列空间与相对可数紧度空间之间的联系.

α-序列空间;β-序列空间; 可数紧度; Pytkeev空间

0 引言

当讨论子空间Y在X中的性质时,Y就是一个相对空间.近年来人们引进了各种各样的相对空间,相对序列空间是其中一类重要的相对空间,它们都属于弱第一可数空间[1].文[2-3]中对几种不同的相对序列空间进行了讨论,并得到了一些重要的结论.本文在此基础上进一步讨论了几类相对序列空间的区别与联系.

1 定义

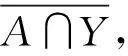
定义2设拓扑空间Y⊂X,若X的子集A集中在Y上且A∩Y∉τc(Y),则在A中存在一个序列收敛于XA中的一点,这时称Y在X中是α-序列空间.

定义3设拓扑空间Y⊂X,若A⊂Y,A∉τc(X)(A∉τc(Y)),则在A中存在一个序列收敛于XA中的一点,这时称Y在X中是序列空间(弱序列空间).

定义4设拓扑空间Y⊂X,若X的子集A集中在Y上且A∉τc(X),则在A中存在一个序列收敛于XA中的一点,这时称Y在X中是β-序列空间.

定义8[7]设X是拓扑空间,Y⊂X,对于序数α,规定[A]α如下：若α=0,[A]0=A；若α=β+1,[A]α={x∈X:在[A]β中存在序列收敛于x}；若α是极限序数,[A]α=∪{[A]β:β<α}.若α=inf{β:x∈[A]β},记α=so(x,A),显然so(x,A)是后继序数.

2 主要结果

在文[2]中，Arhangel’skii提出了这样一个问题：是否存在空间Y⊂X,Y在X中是α-序列空间及序列空间,但Y在X中不是β-序列空间.下面的例1给出了一个肯定的回答.

例1设X=ω1+1,Y={α∈ω1:α不是极限序数},X具有序拓扑.下面证明子空间Y满足条件.

(1)因为Y是离散空间,对于集中在Y上的集合A,A∩Y∈τc(Y),所以Y在X中是α-序列空间.

(2)设A⊂Y,A∉τc(X),则A无限.取αi∈A,i∈N,且当i

(3)设A=ω1,则A集中在Y上且A∉τc(X),但不存在A中的序列收敛于XA中的点,所以Y在X中不是β-序列空间.

我们注意到在例1中，Y在X中不具有可数紧度.但对于β-序列空间结果就不一样了.

定理1若Y在X中是β-序列空间,则Y在X中具有可数紧度.

定理2设空间Y⊂X,若Y在X中每一个包含Y的空间Z中是序列空间,则Y在X中是α-序列空间.

证明设集合A⊂X,A集中在Y上且A∩Y∉τc(X).记Z=X(AY),则Y在Z中是序列空间,所以存在A∩Y中的序列{xi:i∈N}收敛于z∈Z(A∩Y)=XA.故Y在X中是α-序列空间.

下面的例2说明了定理2的逆命题不一定成立.

例2设X={(m,n):m,n∈N}∪{(m,0):m∈N}∪{(0,0)}是Arens空间,即点(m,0)的邻域基为{(m,n)|n>k,k∈N}；

点(0,0)的邻域基为{(0,0)}∪{(n,0),(n,m)|n>k,m>φ(n),k∈N,φ∈NN}；其他点为X的孤立点.

则Y={(m,n):m,n∈N},Z=Y∪{(0,0)}都是X的子空间.因为X是序列空间,所以Y在X中是α-序列空间,但Y在Z中不是序列空间.

定理3设Y是X的闭子集，若Y在X中是弱序列空间，则Y在X中是α-序列空间.

证明设A⊂X,A集中在Y上且A∩Y∉τc(Y),由于Y在X中是弱序列空间，所以有序列{xi:i∈N}⊂A∩Y收敛于点x∈X(A∩Y).又因为Y是X的闭子集，所以x∈Y故x∈XA,因此Y在X中是α-序列空间.

注：由于任意序列空间X的子空间Y在X中是α-序列空间，所以定理3中Y是X的闭子集这个条件不能去掉.

定理4若X是序列空间，X⊂Y,则X在Y中是α-序列空间，但X在Y中不一定是序列空间.

证明设集中A⊂Y,A集中在X上且A∩X∉τc(X).因为X是序列空间，所以有序列{xi:i∈N}⊂A∩X收敛于点x∈X(A∩X)=XA⊂YA.则X在Y中是α-序列空间.令X=ω,Y=ω+1,其中ω,ω+1均具有序拓扑，则X是序列空间，但X在Y中不是序列空间.

定理5若Y在X中是α-序列空间,则Y是Pytkeev空间.

假设x∉[A]ω1.因为[A]ω1集中在Y上且[A]ω1∩Y∉τc(Y),所以存在序列{xi:i∈N}⊂[A]ω1.收敛于y∈X[A]ω1.设αi=so(xi,A),i∈N,β=sup{αi:i∈N},则y∈[A]β+1⊂[A]ω1,矛盾,故x∈[A]ω1.下面用超限归纳法证明Y是Pytkeev空间.

若x∈[A]1,有序列{xi:i∈N}⊂A收敛于x,记Bi={xj:j≥i},则Bi是无限集且{Bi:i∈N}是x在A上的可数π-网.

假设当β<α时,对于x∈[A]β,x在A上具有由无限集构成的可数π-网已证明,下面证明当α=so(x,A)时结论也成立.

由于so(x,A)是后继序数,可设α=γ+1,则存在序列{yi:i∈N}⊂[A]γ收敛于x.由假设知对每个i,yi在A上有由无限子集构成的可数π-网{Bin:n∈N},则{Bin:i,n∈N}是x在A上的由无限子集构成的可数π-网,所以Y是Pytkeev空间.

推论若Y在X中是β-序列空间,则Y是Pytkeev空间.

在定理5中若Y在X中是序列空间,则结论不一定成立.

例3设X=ω1+1,Y={α∈ω1:α不是极限序数}∪{ω1},则Y在X中是序列空间且Y不具有可数紧度；而Pytkeev空间具有可数紧度,所以Y不是Pytkeev空间.

[1] 林寿.广义度量空间与映射[M].北京：科学出版社，1995：84-85.

[2] Arhangel’skii A V，Nogura T.Relative sequentiality[J].Topology and its Applications，1998, 82(1/2/3):49-58.

[3] Arhangel’skii A V.Relative topological properties and relative topological spaces[J].Topology and its Applications，1996, 70(2/3):87-99.

[4] Malykhin V I.Weakly Frechet-Urysohn and Pytkeev spaces[J].Topology and its Applications, 2000,104(1/2/3):181-190.

[5] Pytkeev E G.On maximally resolvable spaces[J].Proc Steklov Inst Math，1984, 4(3):225-230.

[6] 儿玉之宏，永见启应.拓扑空间论[M].方嘉琳，译.北京：科学出版社，2001：294-295.

[7] Tsugunori N,Alexander S.Sequential order of product spaces[J].Topology and its Applications，1995，65(3)：271-285.

ANoteonRelativeSpaces

WANG Han-feng1, LI Jin-jin2

(1.DepartmentofMathematics,ShandongAgricultureUniversity,Taian271018,China; 2.DepartmentofMathematics,ZhangzhouNormalCollege,Zhangzhou363000,China)

An open problem on relative spaces was answered.Some relations among several relative spaces were discussed.At the same time, the relations between relative spaces and the Pytkeev spaces were studied.And the relations between relative spaces and the relative countable tightness spaces were also studied.

α-sequential;β-sequential; countable tightness; Pytkeev spaces

O 189.1

A

1671-6841(2011)03-0019-03

2010-06-18

国家自然科学基金资助项目，编号10971186.

王汉锋(1976-), 男, 讲师, 主要从事一般拓扑学研究，E-mail:whfeng@sdau.edu.cn.