钢带缠绕增强塑料复合软管的有限元分析

方建丰,陈 玲

(1.天津理工大学,天津市复杂系统控制理论及应用重点实验室,天津300384;2.天津理工大学机械工程学院,天津300384)

钢带缠绕增强塑料复合软管的有限元分析

方建丰1,2,陈 玲1,2

(1.天津理工大学,天津市复杂系统控制理论及应用重点实验室,天津300384;2.天津理工大学机械工程学院,天津300384)

提出了一种行之有效的利用有限元法计算螺旋钢带弹性模量的方法,在此基础上,对复合软管整体的单向拉伸、弯曲、扭转载荷下的力学性能进行了数值模拟分析,并与复合软管的实验结果进行了对比,结果表明,数值模拟与实验结果具有较强的一致性,从而验证了数值模拟结果的正确性,为解决复杂结构数值模拟分析中材料属性的确定问题提供了一种有效的方法。

塑料复合软管;螺旋钢带;增强;有限元法

0 前言

复合软管一般是以加强骨架、合成树脂黏结剂和塑料制品经过一定的成型方法制作而成的新型管道[1]。目前,国外一些发达国家的复合软管工业已经发展得相当成熟,已经广泛应用于化工、石油、城市建设等相关领域[2]。但是由于复合软管结构的复杂性,导致无法对复杂工作环境下的复合软管的力学行为进行精确预测,复合软管在使用过程中经常出现由于管内泄露,端部脱扣甚至发生软管爆裂等质量问题[3-4]。目前的传统理论与经验方法尚无法解决此类问题。

本文提出了一种利用有限元法计算螺旋钢带弹性模量的方法,解决了用传统的实验方法难以确定此类螺旋钢带弹性模量的问题。基于上述方法计算出的螺旋钢带的弹性模量,对钢带缠绕增强塑料复合软管的单向拉伸、弯曲、扭转载荷下的力学性能进行了数值模拟分析。为了对数值模拟结果进行验证,分别对复合软管进行单向拉伸、弯曲、扭转实验。

1 问题的描述及材料特性

1.1 钢带缠绕增强塑料复合软管的结构及相关参数

钢带缠绕增强塑料复合软管是由某公司研制的一种新型的钢塑复合软管。这种复合软管以高强度钢带螺旋缠绕形成增强体,以高密度聚乙烯(PE-HD)为基体,并在钢带缠绕时施加预紧力,使得外围的钢带与内部的PE-HD管紧密地连接在一起。钢带缠绕增强塑料复合软管的内部结构共分为5层,包括内管、螺旋钢带、中层包覆、螺旋钢带、外层包覆。复合软管的结构简图如图1所示。

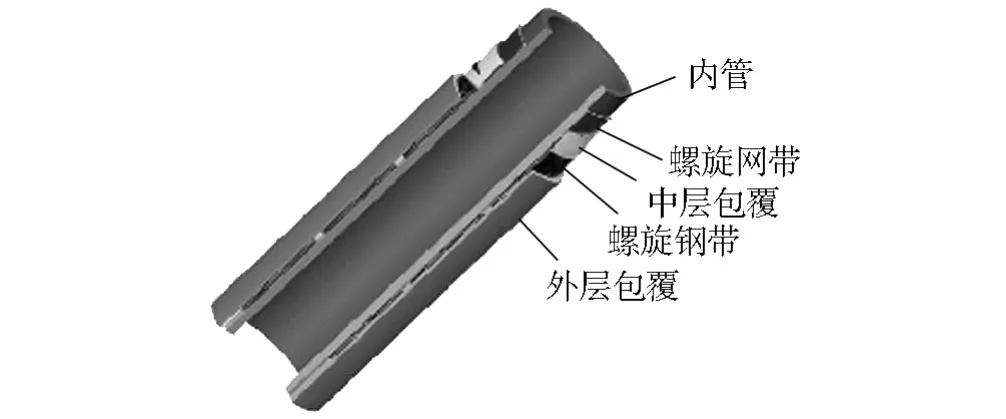
图1 钢带缠绕增强塑料复合软管结构简图Fig.1 The structure diagram of the steel strip winding reinforced plastic composite pipe

1.2 螺旋钢带弹性模量的确定

由于复合软管的螺旋钢带的厚度小于1 mm,而且采用双向螺旋缠绕结构,导致其弹性模量低于常规结构低碳钢材料的弹性模量。因此,需要对螺旋钢带的弹性模量进行重新确定。由于采用传统的实验方法不仅耗时长、成本高,而且其精度难以得到保证,因此本文采用耗时较少、成本较低且精度较高的数值模拟方法。

为了确定螺旋钢带的弹性模量,本文特别设计了一种数值模拟方法,其实验原理如下:

由材料力学可知,单向拉伸实验的变形计算公式为:

式中 A——材料的横截面积,mm2

P——施加的拉力,N

l——模型长度 ,mm

E——材料的弹性模量,MPa

Δl——材料的伸长量,mm

由式(1)可以看出,弹性模量(E)越大,钢带的拉伸变形越小。只要测出一定长度(l)的钢带在轴向力 P的作用下的伸长量Δl(弹性变形范围内),即可计算出钢带的弹性模量。

由式(1)可导出弹性模量计算公式:

根据以上原理,本文利用有限元计算软件ANSYS对螺旋钢带的弹性模量进行数值模拟计算。其有限元模型长度取 l=350 mm,横截面面积 A=1580 mm2;材料为低碳钢,其力学性能参数为 E=2.1×105MPa,泊松比μ=0.3;采用shell181单元进行自由网格划分,其单元数为13808,节点数36137,该单元是4节点单元,每个节点拥有6个自由度,适用于线性、大转动、大应变等非线性问题的求解。螺旋钢带的有限元模型如图2所示。

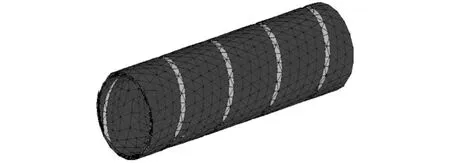
图2 螺旋钢带有限元模型Fig.2 The finite element model of the spiral steel strips

由于各层钢带之间相互接触,为了使模拟更加接近实际,提高计算精度,在每一层螺旋钢带之间均加入面面接触单元,其中,目标面为 TARGE170单元,接触面为CONTA174单元。6层螺旋钢带共有5个接触曲面,划分13203个接触单元。图3为加入接触单元后的螺旋钢带有限元模型。

图3 加入接触单元后的螺旋钢带有限元模型Fig.3 The finite element model within contact elements

由于各层钢带之间尺寸、结构及旋向各有不同,导致每层钢带的变形均不相同,在此采用施加摩擦因数的方法模拟各层间产生的相对滑动。为避免产生刚体位移,在测定弹性模量时,将钢带的一端全部自由度约束,另一端施加沿轴线方向的均布载荷 P,该载荷 P以分步加载方式施加。经过ANSYS求解,可得出各载荷步的相应变形,载荷 P及变形Δl的具体数值如表1所示。

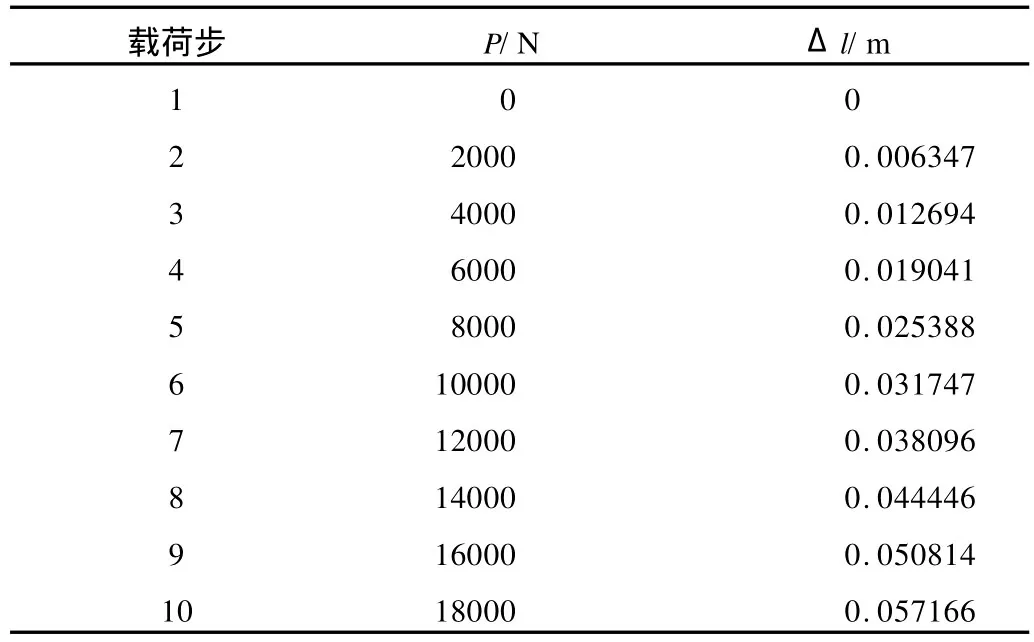
表1 各载荷步载荷 P及相应变形ΔlTab.1 Pand displacementΔl of each load step

将表1中各载荷步下的变形Δl代入式(2)即可求得螺旋钢带的弹性模量。图4是螺旋钢带在各载荷步下计算出的应力-应变曲线。求得该曲线的斜率,即可以确定螺旋钢带的弹性模量 E=0.7×105MPa。

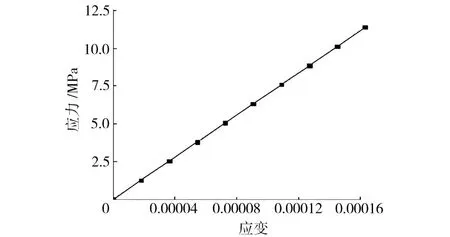
图4 螺旋钢带的应力-应变曲线Fig.4 The stress-strain curve of the spiral steel strip

2 复合软管的力学性能数值模拟

2.1 材料参数及有限元模型

复合软管的整体结构主要采用低碳钢及 PE-HD制成,内管、中层包覆、外层包覆均为 PE-HD,其弹性模量 E=108 MPa,泊松比μ=0.4;复合软管中,螺旋钢带的弹性模量已由本文前述计算得出,即 E=0.7×105MPa,泊松比μ=0.3。为减小模拟计算误差,在建立钢带螺旋缠绕增强复合软管的整体模型时,严格按照该复合软管的设计结构及其外形尺寸精确建立,选择 solid 186单元作为内管、中层包覆、外层包覆模型的单元,选择shell 181单元作为螺旋钢带的单元。网格划分过程中,内管、中层包覆、外层包覆采用映射网格划分;螺旋钢带采用自由网格划分。该有限元模型将用于复合软管的单向拉伸、弯曲、扭转的力学性能数值模拟。复合软管整体有限元模型如图5所示。

图5 复合软管整体有限元模型Fig.5 The finite element model of the whole composite pipe

2.2 复合软管单向拉伸数值模拟及实验验证

2.2.1 单向拉伸数值模拟的边界条件

为了保证单向拉伸计算结果的准确性,在施加边界条件时,尽量选择与实际情况相一致的边界条件。具体做法如下:

(1)考虑软管各层之间的接触作用,除上述计算弹性模量时,在各层钢带之间加入接触单元外,在软管整体结构中的塑料管与钢带之间也引入了面面接触单元,目标面为 TARGE170单元,接触面为 CONTA174单元。并综合考虑单元厚度、时间步长、法向接触刚度以及接触容差因子等因素对计算结果的影响,选择出一组最为合理的参数组合;

(2)为了模拟软管的固定情况,将模型一端所有节点的自由度全部约束;

(3)在模型的另一端施加沿轴线方向的均布载荷。按表2的具体载荷数值,采用分步加载的方式进行加载。

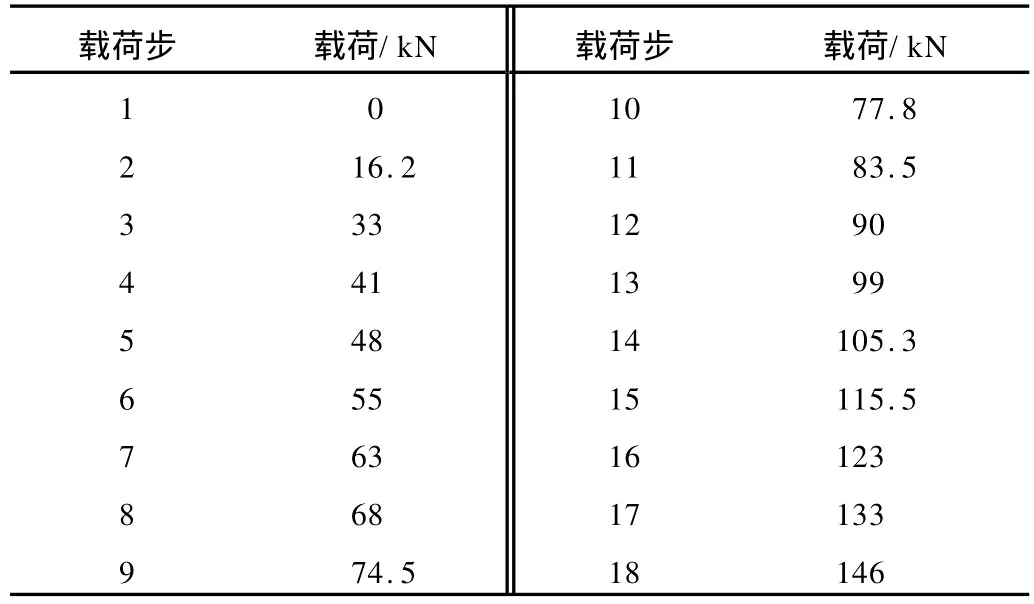
表2 各载荷步的载荷数值Tab.2 The value of each load steps

2.2.2 单向拉伸模拟结果分析及验证

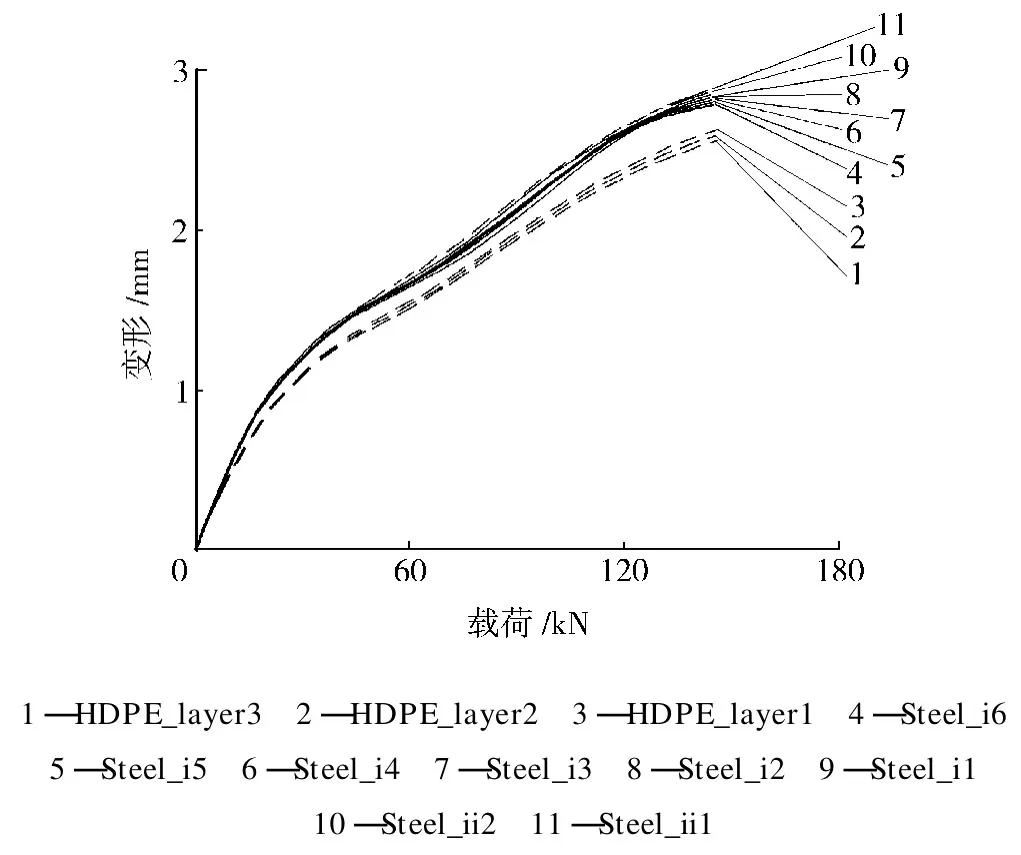
图6 复合软管各层载荷-变形曲线Fig.6 The load-displacement curve of each layer of the composite pipe

图6为选取复合软管内部各层中间位置截面全载荷步的变形响应曲线。从图6可以看出,复合软管在单向拉伸载荷作用下,其内部各层的变形响应趋势基本一致,符合单向拉伸的变形规律;由PE-HD制成的内管(HDPE_layer1)、中层包覆(HDPE_layer2)和外层包覆(HDPE_layer3)的变形比由多层钢带螺旋缠绕制成的螺旋钢带(Steel_i1～i6)及(Steel_ii1～ii2)的变形小,这说明复合软管内部各层所使用的材料不同会导致其抗拉刚度有所差异;此外同种材料制成的不同层之间的变形也有所不同,如:同为 PE-HD的内管、中层包覆、外层包覆,横截面积较小的内管变形较大;而横截面积较大的外层包覆变形较小。这说明同种材料各层的抗拉刚度还与其横截面积的大小有关。

为了验证复合软管单向拉伸模拟结果,选用该型号的复合软管进行单向拉伸实验。使用拉力试验机对复合软管加载,记录符合软管端部的变形值。图7为复合软管整体结构的端部模拟计算的载荷—变形曲线与实验结果的对比图。由图7可知,复合软管在轴向拉力载荷作用下,变形比较均匀,计算值与实验值相比其平均误差仅为4.81%,计算结果与实验结果吻合程度较高,数值模拟结果和实验结果趋势基本一致。

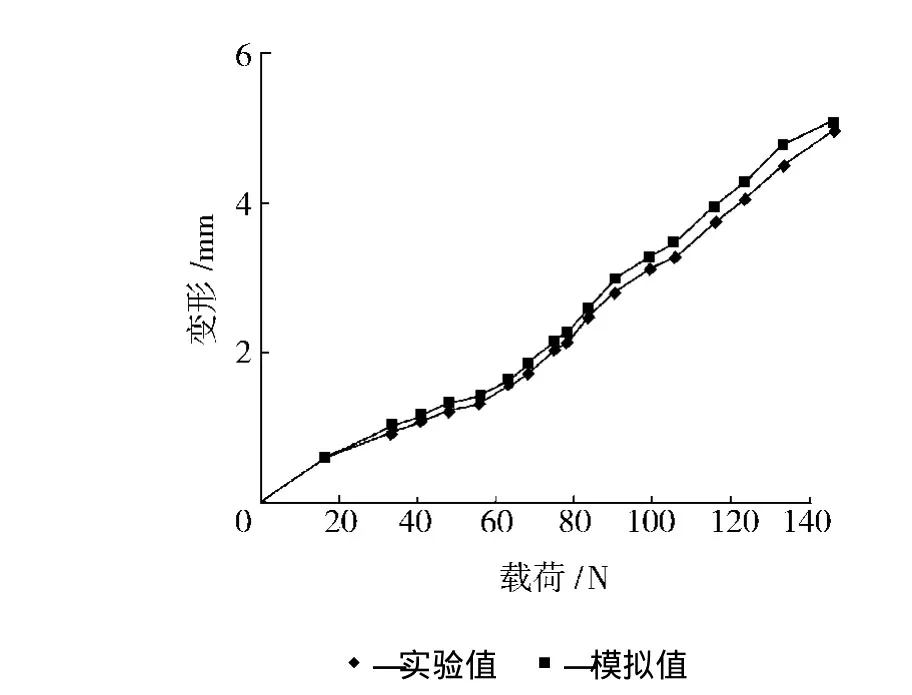
图7 单向拉伸载荷-变形曲线的模拟结果与实验结果的对比Fig.7 Comparison of simulation and experiment of tension load-displacement results

2.3 弯曲与扭转数值模拟结果分析及实验验证

除单向拉伸载荷的数值模拟之外,还对模型施加了弯曲及扭转载荷,其有限元模型的处理方法同上,鉴于篇幅所限,仅给出载荷—变形曲线的模拟结果与实验结果对比。

从图8可以看出,弯曲载荷数值模拟结果与实验结果基本吻合,除第二载荷步计算误差较大以外,其余载荷步计算误差均比较小,数值模拟结果和实验结果趋势基本一致。说明本文所采用的数值模拟方法能够较好地预测复合软管在弯曲载荷下的变形情况。

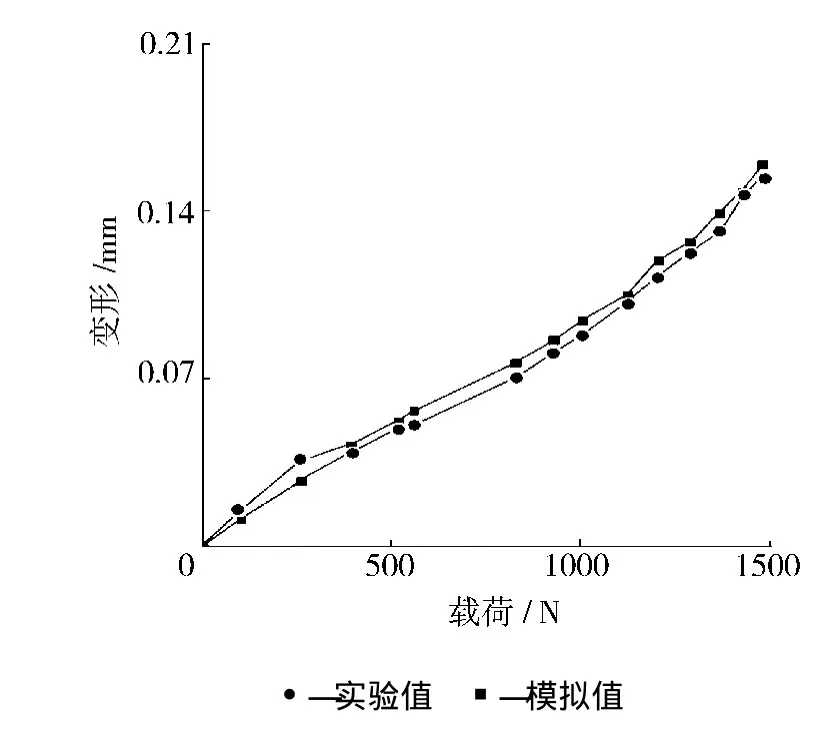
图8 弯曲载荷-变形曲线的模拟结果与实验结果的对比Fig.8 Comparison of simulation and experiment of bending load-displacement results

从图9可以看出,扭转载荷数值模拟结果与实验结果的趋势基本一致,其中除第9至第18载荷步的结果与实验结果误差相对较大外,其他载荷步的结果与实验结果误差均较小。这是由于为了保证数值模拟计算结果比较容易收敛,在给定材料的本构模型时,只考虑其线弹性阶段的本构模型所致。

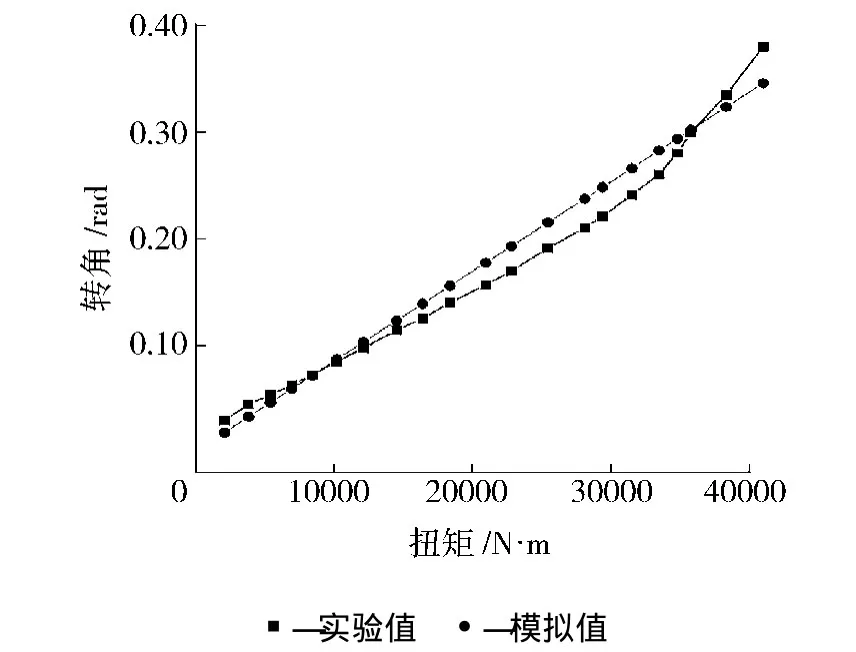
图9 扭转载荷-变形曲线的模拟结果与实验结果的对比Fig.9 Comparison of simulation and experiment of torsion load-displacement results

3 结论

(1)通过结果分析以及与实验结果的对比,证明有限元法可以较好地模拟钢带缠绕增强塑料复合软管在单向拉伸,弯曲及扭转载荷作用下的变形,并且说明本文所采用的数值模拟方法能够较好地预测软管的变形情况;

(2)采用有限元法模拟钢带缠绕增强塑料复合软管单向拉伸、弯曲、扭转实验的精度较高、成本较小,避免了大量重复性的实验。

[1] 程小平.钢骨架增强塑料复合管性能研究[D].杭州:浙江大学机械与能源工程学院,2003.

[2] 郑光明,李秉海,孙晓光.国外复合管的制造和施工技术(一)[J].国外油田工程,2001,17(1):50-54.

[3] 刘辉义,蔡永生,王忠华.国内几种主要给水钢塑复合管材的对比及选择[J].焊管,2005,28(3):24-26.

[4] 林秀锋.钢丝缠绕增强塑料复合管强度分析与优化设计[D].杭州:浙江大学材料与化学工程学院,2006.

FEM Analysis of Steel Strip Winding Reinforced Plastic Composite Pipes

FAN GJianfeng1,2,CHEN Ling1,2
(1.Tianjin Key Laboratory for Control Theory&Applications in Complicated Systems,Tianjin University of Technology,Tianjin 300384,China;2.School of Mechanical Engineering,Tianjin University of Technology,Tianjin 300384,China)

An efficient FEM method for calculating the spiral steel strip′s Young′s modulus was proposed in this paper.Based on the calculation,mechanical properties in three modes,tension,bending and torsion were simulated.The simulation results were in good consistency with the experiment.This method could be applied to determine the material properties of more complex structures.

plastic composite pipe;spiral steel strip;reinforcement;finite element method

TQ320.72+4

B

1001-9278(2011)06-0077-05

2011-01-30

联系人,unver@163.com