线性回归在糖尿病诊断中的应用
胡继礼,杨松涛
(1.合肥工业大学 计算机与信息学院,安徽 合肥 230039;2.安徽中医学院 医药信息工程学院,安徽 合肥 230031)
医院的糖尿病诊断主要靠血糖仪,测血糖较为麻烦,而且容易使糖尿病患者产生恐惧,影响病情.目前,血糖仪的监测结果有时会受到多种原因的影响,诊断不一定准确.本文挖掘了糖化血红蛋白、甘油三酯与空腹血糖数据,分析了糖化血红蛋白、甘油三酯与糖尿病之间的关系.糖化血红蛋白是指血液中所有脂蛋白所含胆固醇的总和.甘油三酯(Triglyceride,缩写TG)[1]是长链脂肪酸和甘油形成的脂肪分子,是人体内最多的脂类.本文通过数据挖掘技术及线性回归算法分析了空腹血糖与糖化血红蛋白及甘油三酯之间的关系,以推动糖尿病的快速诊断,进而提高医生的工作效率.
1 线性回归算法
具有相关关系的变量间虽然不具有确定的函数关系,但通过观测大量的数据,可以发现它们之间存在着一定的统计规律,研究这些统计规律或者研究变量之间相关关系的方法就是回归分析.它能帮助人们有效地从一个可以控制或可以精确观察的变量取得的值去估计另一个随机变量所取的值,如用年龄估计血压.
1.1 线性回归算法的基本原理
线性回归是利用数理统计中的相关分析[2],来确定两种或两种以上变数间相互依赖的定量关系的一种统计分析方法.回归分析的目的是通过具有已知值的变量来预测其他变量的值,找到联系输入变量和输出变量的最优模型.如果在回归分析中,只包括一个自变量和一个因变量,且两者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析.如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析.
一元线性回归用一个主要影响因素作为自变量来解释因变量的变化,在现实问题的研究中,因变量的变化往往受几个重要因素的影响,此时就需要用两个或两个以上的影响因素作为自变量来解释因变量的变化,这就是多元回归,亦称多重回归.当多个自变量与因变量之间是线性关系时,所进行的回归分析就是多元性回归.
设y为因变量,x1,x2,…xk为自变量,当自变量与因变量之间为线性关系时,多元线性回归模型为y=b0+b1x1+b2x2+…+bkxk+e.其中,b0为常数项,b1,b2,…bk为回归系数,b1为x2,x3,…xk固定时,x1每增加1个单位对y的效应,即x1对y的偏回归系数.同理,b2为x1,x3,…xk固定时,x2每增加一个单位对y的效应,即x2对y的偏回归系数,等等.如果两个自变量x1,x2同一个因变量y呈线性相关时,可用二元线性回归模型描述为:y=b0+b1x1+b2x2+e,其中e为误差项.
多元性回归模型的参数估计与一元线性回归方程一样,也是在要求误差平方和为最小的前提下,用最小二乘法求解参数.以二元线性回归模型为例,求解回归参数的标准方程组为:
解此方程可求得b0,b1,b2的数值,亦可用下列矩阵法求得b==(x’x)-1*(x’y),即
1.2 对回归方程进行假设检验
回归系数[3]的计算是依据若干样本实现的,抽样不同会导致所获得的回归系数也不相同,此时需要对回归方程和回归系数进行显著性检验,以检验y和x之间确实存在线性关系.回归方程的显著性检验[4]是利用方差分析所获得的F检验值来检测回归模型总体线性关系的显著性的.对于基于n个样本计算的线性回归关系yi=a+bxi+e,来检验假设:H0∶b=0,如果否定该假设,说明上述模型确实存在;反之,则认为该模型不存在.令
F=U(n-1)/Q,
在H0下F服从自由度为(1,n-2)的F分布[5],根据样本计算F的值,同时查F分布表的自由度为(1,n-2)时1-α分位数的值F0,如果F>F0,则否定了该假设,可认为线性回归关系确实存在.
2 线性回归在糖尿病数据上的应用
将数据挖掘方法引入到糖尿病数据的处理中,根据其数据的特点选用数据挖掘线性回归算法,自动建立线性回归方程,训练系统通过各项参数识别糖尿病因素间的相互关系并判定是否患病.
2.1 数据来源和预处理
本文的实测数据来源于某中医学院附属医院糖尿病研究中心,该数据为病人的体检信息,包括姓名、性别、就诊编号、诊断类型、诊断日期、医生、患者编号、身高、体重、体重指数、心率、尿pH值、尿蛋白24 h定量、尿白蛋白、血红蛋白、空腹血糖、餐后2 h血糖、糖化血红蛋白、C肽胰岛素0、C肽胰岛素30、C肽胰岛素60、C肽胰岛素120、C肽胰岛素180、甘油三酯、高密度胆固醇、低密度胆固醇、载脂蛋白A1、载脂蛋白B、血尿素氮、血肌酐、谷草转氨酶、谷丙转氨酶、GGT、尿酸、C反应蛋白.从中筛选出218条有效数据,删除一些信息不全(有噪音)不利于挖掘的记录,如只有糖化血红蛋白、甘油三酯缺失或者只有空腹血糖、糖化血红蛋白缺失的记录,保留了姓名、性别、患者编号、糖化血红蛋白、甘油三酯和空腹血糖字段.将上述实测数据正确录入后存入数据库作为原始数据,部分体检数据如图1所示.运用数据挖掘技术和线性回归的方法对数据进行预测分析,糖尿病的诊断标准为空腹血糖大于7.0 mmol/L[6].
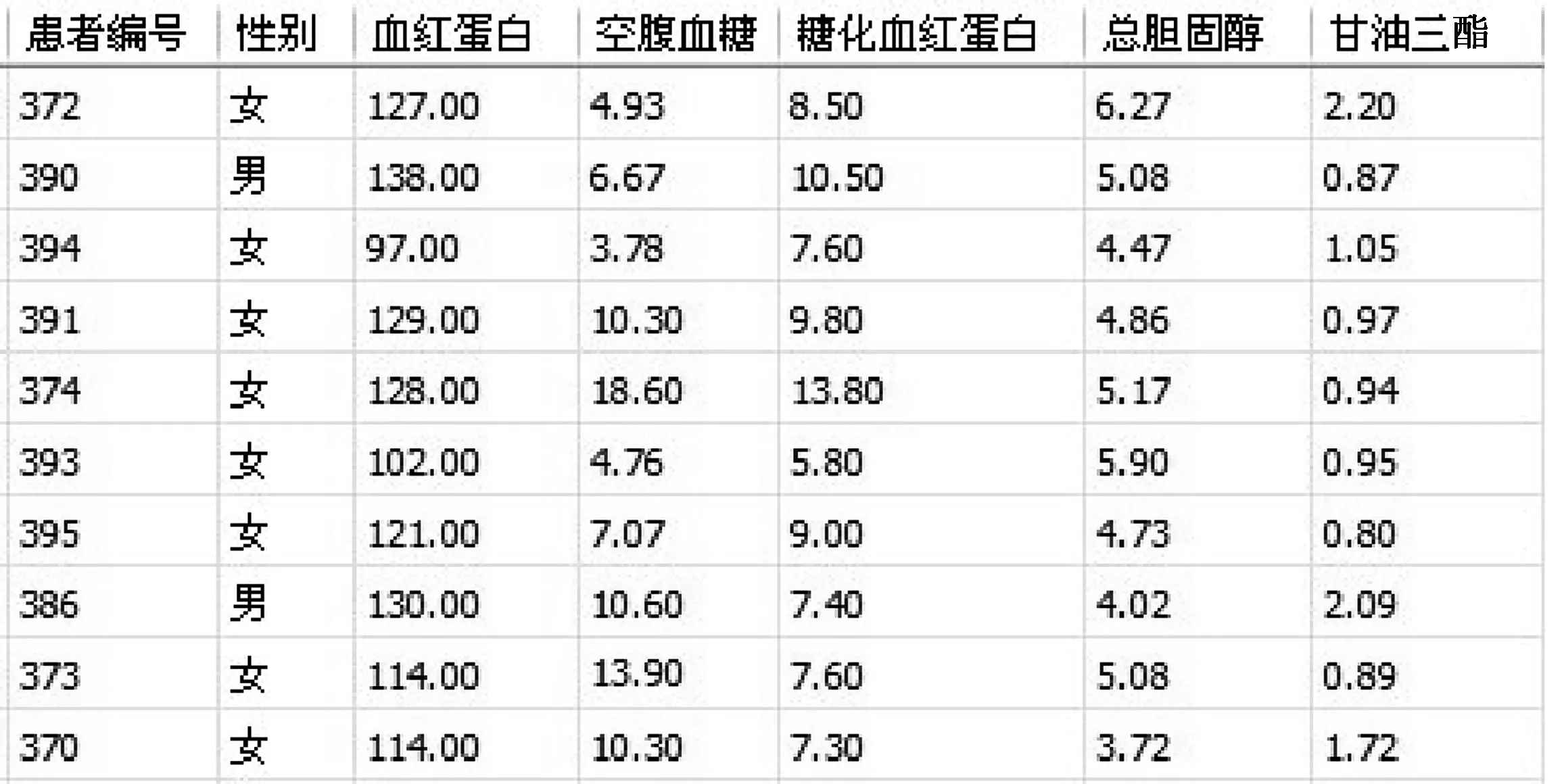
图1 体检数据图Fig.1 Physical examination data diagram
2.2 挖掘工具和环境
以SQL Server 2005的商业智能平台SQL Server Business Intelligence Development Studio(BI)为数据挖掘工具,实验环境是Intel core(TM) i3 CPU M350,Windwos XP Professional版操作系统.
2.3 实验过程
Microsoft SQL Server 2005 Analysis Service(SSAS)提供了Microsoft 线性回归算法[7].Microsoft 线性回归算法是Microsoft决策树算法的变体,其中的MINIMUM_LEAF_CASES参数设置为大于或等于事例总数,事例总数是挖掘模型定型时所用的数据集的总事例数.通过这种方式设置该参数,算法将不创建拆分,从而执行线性回归.创建Analysis Serverices项目,然后创建数据源、数据源视图和用于糖尿病数据的线性回归的挖掘结构.数据挖掘结构建好后,选择所要实验的数据名称,得到如图2所示的界面.
图2 实验所用的数据名称Fig.2 The name of data used in experiment
通过部署和处理挖掘模型,进行数据分析及模型的生成,得到了空腹血糖与糖化血红蛋白和甘油三酯的依赖关系网络[8],如图3所示.
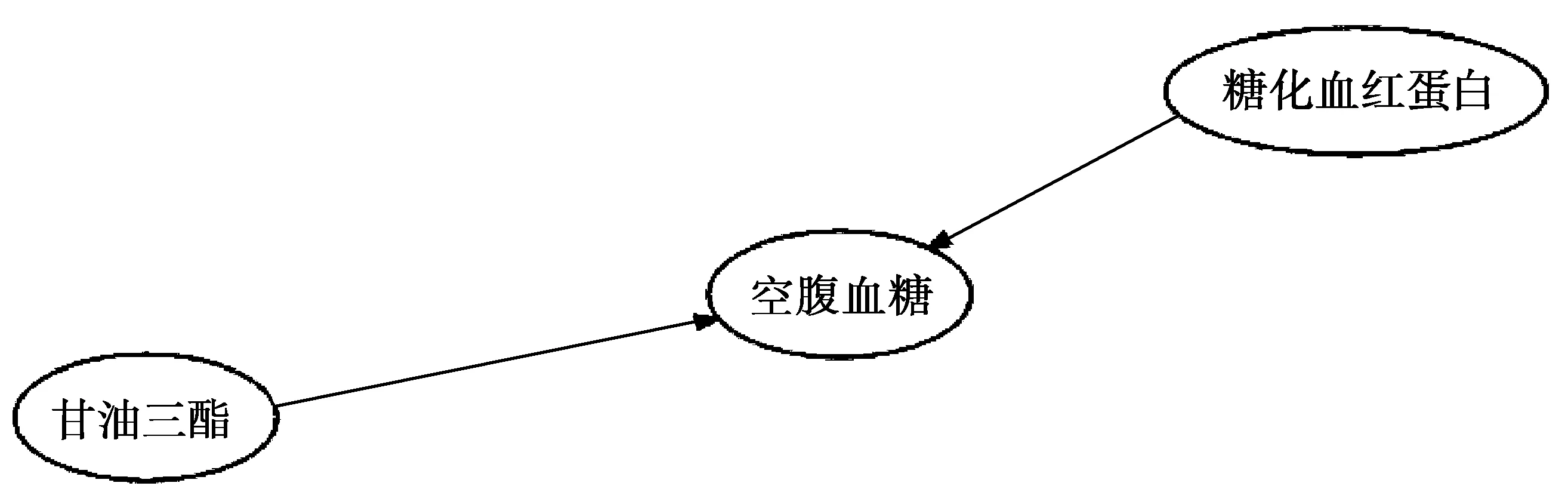
图3 依赖关系网络图Fig.3 Dependency network diagram
也可得到空腹血糖与糖化血红蛋白和甘油三酯的挖掘准确性图,如图4所示.
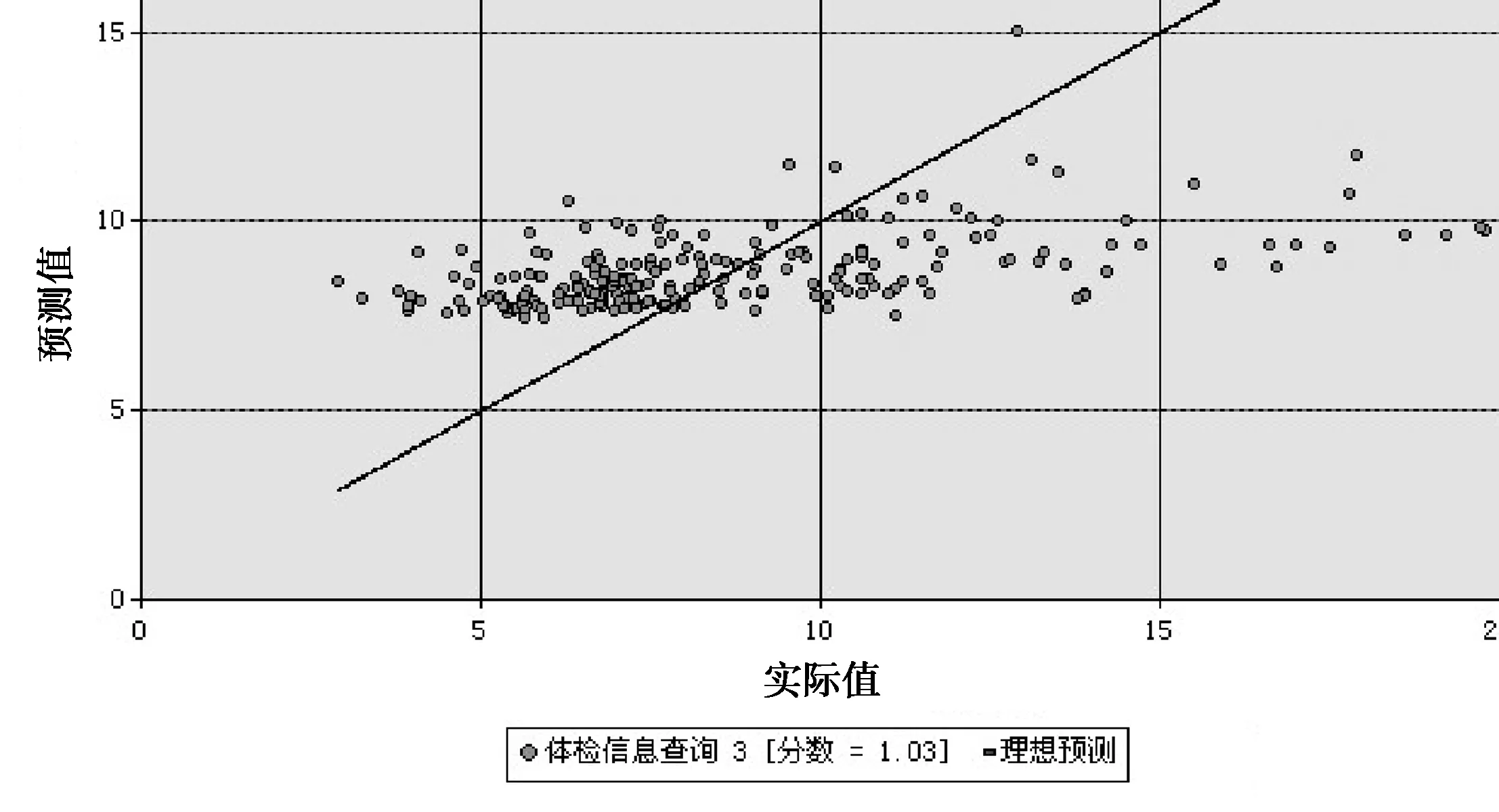
图4 挖掘准确性图Fig 4 Mining accuracy diagram
通过调整Auto_Detect_Periodicity参数,可控制算法找出线性关系的强度,同时经过实验得到空腹血糖与糖化血红蛋白和甘油三酯公式,如图5所示.
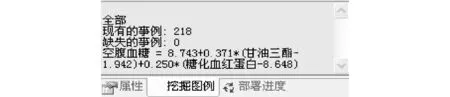
图5 空腹血糖与糖化血红蛋白和甘油三酯公式图Fig.5 Blood sugar and glycated hemoglobin and triglyceride formula diagram
由实验结果可知,空腹血糖与糖化血红蛋白和甘油三酯含有线性关系,糖化血红蛋白和甘油三酯越高,空腹血糖的值越高.当空腹血糖大于7.0 mmol/L时,可判定患者得了糖尿病.
2.4 检验实验结果
本文运用方差分析及概率,对实验结果进行检验,结果越接近1,说明实验结果越准确.在Microsoft SQL Server 2005 Analysis Service(SSAS)数据挖掘窗口输入检测语句:SELECT FLATTENED NODE_DISTRIBUTION AS t FROM [体检信息].CONTENT,得到检测结果,如图6所示.
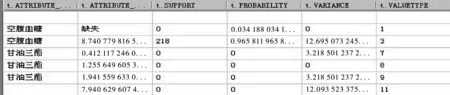
图6 检测图Fig.6 Test diagram
由图6可知,用线性方程空腹血糖=8.743+0.371*(甘油三酯-1.942)+0.250*(糖化血红蛋白-8.648),能得到空腹血糖正确值的概率为0.965 811 965 8…,可证明该实验结果是准确的.
3 结论
本文根据体检病人的信息数据,在数据挖掘技术中运用线性回归算法对数据进行处理,自动生成有价值的、易于理解的线性直线.该直线的特点同目前医学上的认识趋于一致,而且由于该直线是基于实测数据而得的,所以其结果更具实际意义.
用数据挖掘技术分析糖尿病病人的数据,可发现糖化血红蛋白和甘油三酯所含的比例越高,病人的空腹血糖值就越高.医生可以根据糖化血红蛋白和甘油三酯的数据来直接判断病人是否患有糖尿病,这样可以提高医生的工作效率,也节约了医院成本,减轻了病人的经济负担.将数据挖掘技术引入到糖尿病数据的处理中,为探讨2型糖尿病发病的相关因素之间的相互影响以及之间的规律或规则提供了一种新的方法和手段.
参考文献:
[1] 罗森林,成华.数据挖掘在2型糖尿病数据处理中的应用[J].计算机工程与设计,2004,25(11):1889-1892.
[2] 孟小东,袁道华.基于回归模型的数据挖掘研究[J].计算机工程与现代化, 2010, 23(1): 26-28.
[3] 罗森林,张铁海.知识发现在2型糖尿病数据处理中的应用研究[J].计算机工程与应用,2004,17(23):199-201.
[4] 马亮亮,田富鹏.基于多元线性回归模型的海西州地区糖尿病发病情况研究[J].伊利师范学院学报,2010,6(2):38-40.
[5] 龚著琳,陈瑛.数据挖掘在生物医学数据分析中的应用[J].上海交通大学学报,2010,30(11):1420-1423.
[6] 陈涛,曹瑞峰.糖尿病患者尿微量白蛋白与脂质、胰岛素和糖化血红蛋白的相关性研究[J].国际检验医学杂志,2006,27(3):278-279.
[7] Mac Lennan,Tang Z H.数据挖掘原理与应用——SQL Server 2008数据库[M].董艳,译.北京:清华大学出版社,2010.
[8] 周怡,王世伟.医学数据挖掘——SQL Server 2005案例分析[M].北京:中国铁道出版社,2008.
——与非适应性回归分析的比较

