GPS整周模糊度搜索算法的可靠性和时效性比较*

夏传甲

(中国地震局地震研究所，武汉 430071)

GPS整周模糊度搜索算法的可靠性和时效性比较*

夏传甲

(中国地震局地震研究所，武汉 430071)

研究了GPS载波相位快速静态定位中的整周模糊度搜索算法，对实数编码的改进遗传算法和LAMBDA算法进行了对比分析。算例表明：实数编码的遗传算法在搜索效率和可靠性方面和LAMBDA算法相当。

整周模糊度;LAMBDA算法;遗传算法;实数编码;模糊度搜索

1 引言

GPS载波相位快速静态定位的关键是整周模糊度的固定，这是近年来国内外GPS研究中一个非常活跃的领域［1-5］。其核心问题就是整周模糊度搜索算法的可靠性和时效性。算法的可靠性关系到整周模糊度固定的正确与否，只有固定到正确的整周模糊度，才能将载波相位观测值转化为高精度的距离观测值，进而获得高精度的点位信息;算法的时效性关系到整周模糊度固定的效率，进而影响GPS快速静态定位的效率，因而整周模糊度固定的可靠性和时效性决定了GPS快速静态定位的精度和应用范围，具有重要意义［6-10］。

整周模糊度搜索算法的可靠性和时效性与搜索空间［6］及搜索方式［11］有关，搜索空间的构造一定要保证搜索结果的可靠性，而搜索方式的选择一定要兼顾搜索的效率，因此搜索空间的构造和搜索方式的选择是相互关联的。本文研究了整周模糊度搜索算法的构造空间和搜索方式，分析了其特点并加以分类。并以LAMBDA算法［4，5］和实数编码的改进遗传算法［11］为研究对象，对其可靠性和时效性做了对比分析。

2 整周模糊度的搜索空间

整周模糊度的固定是一个从实数解到整数解的映射过程，是多对一的映射模式，由于没有确定的数学解析式来构建实数解和整数解的关系，只能将候选值组合带入目标函数［1］，满足条件的组合就是所求的整周模糊度。对于目标函数而言，如果对整周模糊度的所有组合不限定条件，搜索的组合数将非常大，对搜索效率影响很大，因此需要对整周模糊度的组合加以限制，限制的过程就是构造搜索空间的过程。构造的搜索空间需要满足两个条件：

1)在搜索空间上的搜索等于在整个整数空间搜索，也就是说搜索空间必须包括满足搜索准则的那一组整周模糊度，这个条件决定了整周模糊度解算结果的可靠性。

2)搜索空间必须尽量的小，这个条件决定了整周模糊度搜索的效率。

显然，搜索算法的可靠性与时效性是相矛盾的。对于每一个整周模糊度的浮点解，构造整数空间［-d+d］，d是任意的大于零的整数，那么对于n个整周模糊度而言，就是一个以为中心的n维空间多面体，在满足条件1)的前提下，搜索效率非常低。如果利用整周模糊度浮点解的协方差阵，则构造搜索空间［-σ0qi，+σ0qi］，这是对n维空间多面体的限制，从n维空间变成有限的空间，缩小了搜索的范围，在保证可靠性的前提下，提高了搜索的效率，因此从统计检验的角度出发，划定搜索范围是构造搜索空间的一个办法。在此基础上，FARA算法［1-3］通过两两模糊度参数的相容性检验，排除不可能的候选值组合，进一步限定搜索的空间，提高了搜索的效率。这种以整周模糊度浮点解为中心，根据置信区间构造搜索范围并利用整周模糊度参数间的相容性来加以限制的方法的思想在其他方法中得到了很多应用，比如Cholesky分解法等;遗传算法［6-10］以整周模糊度的浮点解和协方差阵条件，利用统计检验的方法确定整周模糊度的范围，完成编码工作，然后通过选择，杂交和变异完成遗传过程; FASF算法［1-3］中，每一个整周模糊度的搜索范围的确定是在其左边模糊度序列固定的基础上平差得到的，也就是说FASF(Fast Ambiguity Search Filter)方法每固定一个整周模糊度，就要平差一次来固定下一个整周模糊度，平差得到整周模糊度的浮点解称为条件估值，协方差称为条件方差，此时以条件估值为中心，以条件方差来划定置信区间形成搜索空间。

LAMBDA算法的思路和上述方法都不同。它不是从统计检验的角度构造搜索空间，而是从目标函数入手。它首先对目标函数设定了合理的范围，然后对目标函数进行矩阵分解，得到条件估值和条件方差，形成以条件估值为中心，条件方差来确定半径的搜索椭球，那么LAMBDA算法就将n维立体空间变成了搜索椭球，缩小了搜索的范围，提高了搜索效率。

基于上面的分析，对基于模糊度域的搜索算法进行分类(表1)。

表1 基于搜索空间的搜索算法分类Tab.1 Classification of algorithms based on search space

以二维整周模糊度浮点解和协因数阵为例，分析了改进遗传算法和LAMBDA算法在构造空间上不同。

通过LAMBDA算法处理后得到(没有进行降相关处理)：

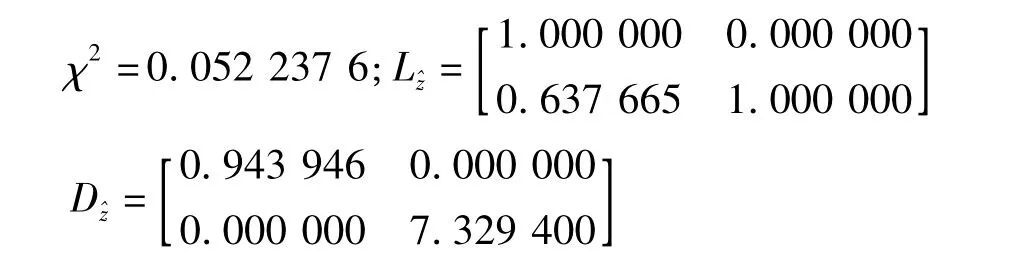
图1 改进的遗传算法的搜索空间Fig.1 Search space of the improved genetic algorithm

图2 LAMBDA算法构造的搜索空间Fig.2 Search space of the LAMBDA

通过二维实例分析：以置信区间构造的搜索空间是一个矩形，而从目标函数出发构造的搜索空间是一个椭圆。在参数估计中，一个n维的整周模糊度向量服从正态分布，以FARA算法为例，每一个整周模糊度的置信度为1-α，也就是取值正确的概率为P=1-α，假设整周模糊度之间的相关性为0，整周模糊度向量取值正确的概率为P=(1-α)n＜1，因此根据置信区间构建的搜索空间取值正确的概率总小于1，但是改进遗传算法的搜索成功率除了和初始种群有关，选择杂交和变异也是重要的影响因子，并且遗传过程是一个循环迭代的过程，所以取值正确的概率不是总小于1。

根据目标函数构建的搜索椭球的大小取决于χ2，只要χ2使得搜索椭球至少包含一个整周模糊度向量候选值，那么一定包含满足目标函数最小的组合，也就是说在搜索椭球的搜索等于在整数空间内的搜索，取值正确的概率总等于1，因此χ2的选择至关重要。

3 整周模糊度的搜索方式

在整周模糊度向量的搜索空间确定以后，只是得到了整周模糊度向量的候选值，此时整周模糊度向量的搜索变成了从整数空间到整数空间的多对一的映射关系，函数关系仍然没有变化。

对于目标函数而言，没有确定的数学解析式，无法完成整周模糊度向量从整数空间到整数空间的多对一的映射。在FARA算法中，在确定整周模糊度向量的搜索范围后，整周模糊度的候选值候选值将有sum＞mn个组合，将其逐一带入目标函数，满足条件的组合就是所求的整周模糊度向量。在LAMBDA算法中，将目标函数进行矩阵分解得到条件估值和条件方差，然后按照序贯条件平差得到整周模糊度向量的搜索范围，从第n个整周模糊度的固定开始一直到第一个整周模糊度，前面的整周模糊度的选择影响了后面的整周模糊度的搜索中心和搜索范围，通过这种序贯方式满足条件的组合就是所求的整周模糊度向量。在FASF算法中，从第一个整周模糊度开始，每固定一个整周模糊度后，带回整数最小二乘估计中，得到新的整周模糊度向量的条件估值和条件方差，以条件估值为中心，条件方差为置信区间构建搜索空间得到第二个整周模糊度的候选值，再固定第二个整周模糊度，以此类推通过这种回归算法，满足条件的组合就是所求的整周模糊度向量。

遗传算法属于人工智能的实现算法中的一种，它模仿生物优胜劣汰的进化机制进行逐次，并行的迭代。遗传算法经过编码和解码过程，实际上是将由置信区间构建的整周模糊度向量转化为染色体，此时对整周模糊度的搜索实际上是对染色体上基因的选择问题，然后通过选择、杂交和变异等过程产生新的染色体，此时满足评价标准的染色体就是所求的新一代，然后通过不断地循环得到最终的染色体，经过解码后得到整周模糊度向量。

根据搜索方式对基于模糊度域的搜索算法进行了简单的分类(表2)。

表2 基于搜索方式的搜索算法分类Tab.2 Classification of algorithms based on search pattern

4 搜索算法的可靠性分析

实验数据来自于2010年4月9号在武汉地震计量检定与测量工程中心采集的4个小时的采样率是1 s的静态观测数据。数学模型采用短基线载波相位双差定位模型，这种模型可以消除与距离有关的误差项。实验中比较了LAMBDA算法和实数编码的改进遗传算法的可靠性和时效性。

利用teqc对原始数据进行预处理，数据采样率为10 s，卫星高度角是15°，每隔10分钟截取一段数据，每段数据取6个历元为一小段进行计算。选用L1观测值，总计40次，前24次共有7个卫星对，后16次共有5个卫星对(表3)。

由表3可知，LAMBDA算法和改进遗传算法大部分都能固定整周模糊度，但是也有少数例外：

1)LAMBDA算法搜索到了椭球区间内的错误的整周模糊度组合，这说明LAMBDA算法所采用的基于目标函数构建的搜索椭球没有包含正确的整周模糊度组合，这也说明了虽然理论上在搜索椭球的搜索等于在整数空间内的搜索，搜索成功的概率等于1，但是由于χ2设置问题，并不能保证搜索椭球一定包含正确的整周模糊度向量候选值，这就导致了LAMBDA算法固定了错误的整周模糊度组合。

2)改进的遗传算法搜索到了置信区间内的错误的整周模糊度组合，这表明在置信区间内的搜索不等于在整数空间内的搜索，FARA算法，FASF算法和遗传算法的实例已经说明了这点［11］。

3)当卫星数目发生变化时直接导致模糊度浮点解发生波动从而影响两种算法不能固定整周模糊度。这主要是估计参数的精度受到观测条件的影响，例如卫星接收机几何条件变化、观测值类型、卫星数目、采样率等。

4)两种算法的实验对比来看，虽然LAMBDA算法从理论上来说优于改进的遗传算法，也就说在椭球内的搜索优于在置信区间内的搜索，但是由于改进的遗传算法是一种全局最优化搜索算法，在编码和搜索方式上的特点导致了和LAMBDA算法的搜索效果相当。

表3 两种算法处理结果对比Tab.3 Comparison between the results from two algorithms

5 搜索算法的时效性分析

利用teqc对原始数据进行预处理，数据采样率为10 s，卫星高度角为15°，参考卫星为15，其余分别为18、21、22、24、26和27。利用单历元模型，选用L1观测值，总计50个历元(表4和图3)。

表4 两种算法搜索时间的比较Tab.4 Comparison of search time between two algorithms

图3 LAMBDA算法和改进遗传算法搜索时间变化图Fig.3 Search time of LAMBDA and an Improved algorithm based on real coding

根据实验结果的统计分析，可以得出：

从搜索时间的统计意义上来看，LAMBDA算法和改进遗传算所需时间相当。

从搜索时间的稳定性来看，LAMBDA算法的稳定性稍好于改进的遗传算法。

通过分析可以得到搜索算法的时效性受到下列因素的影响：

1)搜索算法的时效性与搜索空间的大小有关。对LAMBDA算法而言，经过整周模糊度降相关处理后，其相关性被降低，条件数被减小。由目标函数确定的椭球的大小取决于χ2，通过控制χ2的大小可以控制搜索椭球包含候选值的个数，所以LAMBDA算法的搜索时间大致相等，并且比较快;对于改进的遗传算法而言，利用浮点数编码使得所求的参数没有增加，且占用计算机内存少，并且在杂交过程中巧妙地利用杂交前后两个整周模糊度向量之和不变，且子代的最值为父代取或的值，最小值为父代取与的值的特点，在这个最大最小范围内随机产生一个子代，另一个子代则利用它们之和不变的性质来确定，从而代替二进制中的杂交，提高了杂交过程的效率，所以改进的遗传算法的搜索时间和LAMBDA算法相当并且也比较稳定。

基于以上分析，我们可以得到：基于目标函数的Cholesky分解构造搜索空间的LAMBDA算法，可以从整体上控制模糊度候选值的个数，从而使搜索时间保持稳定的水平;基于置信区间的改进遗传算法，虽然初始种群变化较大，但是利用浮点数编码大大缩小参数个数，并且利用了杂交过程中特点使得搜索时间整体波动不大。

2)搜索算法的时效性与搜索方式有关。LAMBDA算法的搜索方式是序贯平差，前面的部分模糊度参数的选择，通过参数估计直接影响了后面的模糊度参数的搜索范围，这就是LAMBDA算法构造的以条件参数为中心，由条件方差和决定大小的搜索椭球，条件参数的确定利用了模糊度参数间相关性，充分考虑了前面模糊度参数对后面模糊度参数的综合影响，这样使得搜索椭球的中心更加精确，同时条件方差和原始方差相比也大大减小。改进遗传算法的搜索方式是人工智能，通过选择，杂交和变异等遗传过程形成下一代的种群，这是模仿生物优胜劣汰的进化机制。这种搜索方法综合考虑了各种因素，是一种优化搜索方式，它不仅考虑了模糊度参数间的相关性，而且考虑了各种偶然因素，因此改进的遗传算法和LAMBDA算法的执行效果是相当的。

6 结语

在函数模型和随机模型相同时，不同的搜索方法可能得到不同的整周模糊度整数解。通过对搜索空间和搜索方式的分析得到：基于目标函数构建搜索空间的LAMBDA算法的可靠性优于基于置信区间构建搜索空间的FARA和FASF算法［6］，基于序贯方式的LAMBDA算法的时效性优于基于逐一带入方式的FARA算法和基于回归方式的FASF算法［6］，而实数编码的改进遗传算法在可靠性和时效性方面和LAMBDA算法相当，本文研究表明以目标函数构造搜索范围的搜索算法的可靠性和时效性不一定优于基于置信区间的搜索算法。

1 刘基余.GPS卫星导航定位原理与方法［M］.北京：科学出版社，2006.

2 李征航.GPS测量与数据处理［M］.武汉：武汉大学出版社，2005.

3 刘大杰.全球定位系统的原理与数据处理［M］.上海：同济大学大学出版社，2003.

4 Teunissen P J G.Theleast-squares ambiguity decorrel-ation adjustment：a method for fast GPS integer ambiguity estimation［J］.Journal of Geodesy，1995，70：65-82.

5 Jonge de，The LAMBDA method for integer ambiguity estimation：implementation aspects［J］.Delf Geodetic Computing CentreLGR Series，1996，(12)：562.

6 李淑慧，等.基于搜索空间构造模糊度搜索方法的可靠性［J］.测绘学院学报，2004，21(1)：11-13.

7 刘智敏，等.遗传算法解算GPS短基线整周模糊度的编码方法研究［J］.武汉大学学报(信息科学版)，2006，31 (6)：607-610.

8 刘智敏，等.基于遗传算法的高精度GPS相对定位解算研究［J］.测绘通报，2007，6：1-3.

9 刘智敏，等.基于遗传算法的GPS单历元单点定位方法研究［J］.武汉大学学报(信息科学版)，2007，32(1)：35 -38.

10 LiZuofa.Efficient ambiguity search using genetic algorithms［C］.ION GPS-95，California，1995.

11 夏传甲.GPS短基线整周模糊度搜索算法的研究与实现［D］.中国地震局地震研究所，2011.

COMPARATIVE ANALYSIS OF RELIABILITY AND EFFICIENCY OF GPS AMBIGUITY ALGORITHM

Xia Chuanjia
(Institute of Seismology，CEA，Wuhan 430071)

The carrier phase ambiguity of GPS fast static positioning technique is studied，and the comparative analysis of LAMBDA and the improved real-coded genetic algorithm is made.The computation results show that the two algorithms have similar performance.

integer ambiguity;LAMBDA(Leact-squares Ambiguity Decorrection Adjustment)algorithm;genetic algorithm;real-coded;ambiguity search

1671-5942(2011)Supp.-0077-05

2011-01-26

国家自然科学基金(40974011);中国大陆构造环境监测网络

夏传甲，男，1984年生，硕士，主要研究方向为GPS算法的研究及其在大地测量学中的应用.E-mail：xiachuanjia@163.com

P207

A