基于多元联系数集对分析模型的高校实验教学质量评价
陶利民,徐真真
(1.杭州师范大学杭州国际服务工程学院,浙江 杭州 310012;2.浙江工业大学信息工程学院,浙江 杭州 310023;3.浙江农林大学艺术设计学院,浙江 杭州 311300)
基于多元联系数集对分析模型的高校实验教学质量评价
陶利民1,2,徐真真3
(1.杭州师范大学杭州国际服务工程学院,浙江 杭州 310012;2.浙江工业大学信息工程学院,浙江 杭州 310023;3.浙江农林大学艺术设计学院,浙江 杭州 311300)
文章根据实验课教学的特点,分析、确定了实验课程的课堂教学质量评价指标体系,建立了一种基于多元联系数集对分析的综合评价新模型.并通过实例研究了评价效果,评价结果合理可靠.为高校实验教学质量综合评价提供了一种新的方法和思路.
多元联系数;集对分析;实验教学;评价模型
0 引 言
实验教学是高校理工科教学的一个重要组成部分,对培养学生的动手能力、独立分析问题及解决问题等方面能力起到重要作用,是培养学生综合素质和创新能力的重要途径之一.一般来说,实验课教学过程既包括教师的教与学,也包括学生的动手练习.充分考虑及利用实验课教学特征,研究适合于实验课教学特点的评价方法是非常必要的.实验教学评价由于评估者的水平和评估角度有异,所谓“好”“较好”并无明显数量界限,或者说带有一定模糊性,因而不同的人对同一因素的评估结果可能不尽相同.考虑到影响实验课教学质量的指标具有模糊性,用统计学的方法确定这些因素的具体判断值很难,因此笔者试图将多元联系数引入到实验课教学效果评价当中来解决这个问题.由我国学者赵克勤提出的集对分析及其联系数在表示由随机、模糊、不确知等不确定性导致的综合不确定问题方面有独到之处.
1 集对分析与多元联系数
集对分析[1]20-21(Set Pair Analysis,简记为SPA)是我国学者赵克勤于1989年提出的一种全新的研究确定与不确定性理论方法.它的核心思想是将确定与不确定视为一个系统,从事物之间的联系与转化的同一度、差异度和对立方面刻划事物.集对及联系数构成集对分析的基本概念.集对实际上就是具有一定联系的两个集合所组成的一个对子.集对分析则是对两个集合的特性作出对立同一分析,主要数学工具是联系数.集对的特性用联系数进行定量刻划.
定义1[1]34-35给定两个集合A和B,它们组成集对H=(A,B),在某一具体问题背景W下,对集对H的特性展开分析,设集对H所具有的特性总数为N,其中在S个特性上为两个集合所共同具有,在P个特性上两个集合相互对立,在其余F=N-S-P个特性上两个集合既不相互对立又不为这两个集合所共同具有,称
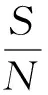
(1)
为集对H=(A,B)在问题背景W下的联系数.
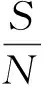
μ=a+bi+cj
(2)
式中,a称为同一度,表示两个集合的同一程度;b称为差异度(不确定度),表示两个集合的差异不确定程度;c称为对立度,表示两个集合的对立程度;a,b,c∈[0,1]为实数,且满足归一化条件a+b+c=1;i为差异度系数,一般i∈[-1,1],视不同情况取值;j为对立度系数,规定其恒取值-1.这种刻划事物确定与不确定的定量描述,是从事物的同(同一)、异(差异)、反(对立)3个方面反映不确定性.因此,式(2)又称为同异反联系数或三元联系数,它已经广泛地应用在各个领域.但在实际应用中,要用到多元联系数或比三元更高的联系数.
定义2[1]57多元联系数是在同异反联系数μ=a+bi+cj的基础上对bi项进行推广与扩展后形成的一种联系数.其一般形式是
U=A+B1i1+B2i2+…+Bnin+Cj
(3)
一般地,当n=k时,称为k+2元联系数,当k≥2时的联系数称为多元联系数.下面以四元联系数为例说明,其它多元联系数类似.
对于四元联系数,其一般形式为U=A+Bi+Cj+Dk
(4)
其中A,B,C,D为正实数,通常,称多元联系数中的A、B、C、D为联系分量,而i、j、k为联系分量系数.通常情况下,多元联系数中最后一个联系分量系数恒取值-1.取N=A+B+C+D,称N为联系范数,用N除式(4),并令
μ=U/N,a=A/N,b=B/N,c=C/N,d=D/N
此时式(4)可以表示为
μ=a+bi+cj+dk
(5)
式(5)即为四元联系数,式(5)中a,b,c,d∈[0,1],且a+b+c+d=1.在不具体说明的情况下,i,j,k仅作为标记使用.
在实际研究工作中,可以比较方便地确定出四元联系数表达式.例如一个方案H让10位专家进行评判,如果有4位认为优,3位认为良,2位认为中,1位认为差,则评判结果可表示为如下四元联系数:
U=4+3i+2j+1k
将其归一化后为:
μ=0.4+0.3i+0.2j+0.1k
2 多元联系数集对模型及评价
进行实验教学评价的时候,由于评价对象的相关指标有很多,要想合理地定出权数分配,是很困难的.难以真实地反映各因素在整体中的地位.此时,宜采用多级模型的评价方法.在此采用二级模型评价.
2.1 确立评价对象的评价指标集U
被评价对象的各指标构成的集合为U={U1,U2,…,Un},其中,元素Ui(i=1,2,…,n)就是影响评价对象的各种因素.在不同的场合,也将其称为质量指标或参数指标,这些因素能综合反映出对象的质量,人们将这些因素作为评价对象的依据.
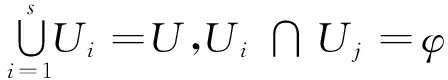
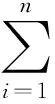
理工科专业中包含有实验课的课程很多,在此以计算机应用基础课程为例进行说明,当然对于其它课程也有参考意义.综合考虑课程特点,借鉴文献[2][3]形成如表1所示的实验教学质量评价指标体系,其评价指标集U可由4个子指标集组成,U={U1,U2,U3,U4}.
其中,U1={U11,U12,U13,U14};U2={U21,U22,U23,U24,U25};U3={U31,U32,U33,U34};U4={U41,U42,U43,U44}.各评价指标的具体含义见表1.

表1 实验教学质量评价指标体系[2-3]
2.2 建立评价集V
组成评语的集合为V={v1,v2,…,vm}.其中,元素vj(j=1,2,…,m)就是各种可能的评价结果,它可以是模糊的,也可以不是模糊的.不过,vj对V的关系是明确的.如表1所示,一个评价集就由评价指标的各种等级组成.在此采用4个评价等级,即V={v1,v2,v3,v4}={优,良,中,差}.
2.3 建立各评价指标的权重集W
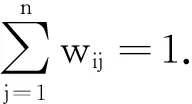
W1=(0.25,0.25,0.25,0.25);W2=(0.20,0.21,0.21,0.21,0.17);W3=(0.26,0.26,0.26,0.22);W4=(0.25,0.25,0.25,0.25).
2.4 建立单指标评价矩阵R
进行评价时,从评价指标集中一个因素Ui出发,以确定评价对象相对于评价集元素vj(j=1,2,…,m)的属于程度rij(j=1,2,…,m),称为单因素评价.对第i个因素Ui评价出来的结果Ri称之为单因素评价集,Ri=(ri1,ri2,…,rin).

学期结束时,让学生、教学管理部门填写调查问卷对该课程实验教学质量进行评估,即让学生和各部门在评价集V={优,良,中,差}上针对各指标给出等级.然后对问卷进行统计,根据统计结果建立以下4个方面的评价矩阵,包括教学环节、教学方法、教学效果、教学管理.
最后,得到关于U1,U2,U3,U44个因素组的评价矩阵分别为:
说明,以R1中对评价指标U11的评价向量为例.从上面可以看出其评价向量为(0.605,0.213,0.152,0.030),表示在调查人员中,对于该实验内容是否服从于培养目标状况,有60.5%的人给出的评价等级为优;有21.3%的人给出的评价等级为良;有15.2%的人给出的评价等级为中;有0.3%的人给出的评价等级为差.用四元联系数可表示成:
μ(U11)=0.605+0.213i+0.152j+0.030k
对其它评价指标的评价向量都可作同样理解.
2.5 根据评价集中的评价等级确定用几元联系数
在此采用评价集V={v1,v2,v3,v4}={优,良,中,差},有4个评价等级.因此,采用四元联系数.
2.6 一级模型评价
对于每个子集Ui,按一级模型进行评价:
Bi=WiRi=(bi1,bi2,…,bim) (i=1,2,…,s)
(6)
根据式(6)计算出B1,B2,B3,B4:
B1=W1R1=(0.643,0.213,0.114,0.030);B2=W2R2=(0.515,0.191,0.158,0.136);
B3=W3R3=(0.565,0.224,0.172,0.039);B4=W4R4=(0.704,0.190,0.091,0.015)
2.7 二级模型评价
构建评价矩阵R,其方法是将每一个Ui作为一个元素,并且用Bi作为它的单因素评价.
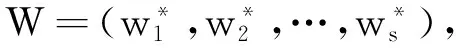
这样就有第二级的综合评判,计算综合评价多元联系数μ[4]:
μ=WRE
(7)
式(7)中E为多元联系分量系统矩阵.
根据式(7)计算出综合评价多元联系数μ:

=0.607+0.202i+0.132j+0.059k
2.8 利用联系数μ来进行综合评价[5-6]
2.8.1 根据“均分原则”确定四元联系数的联系分量取值并计算评价对象的联系数值
根据集对分析理论给三元联系数μ=a+bi+cj的规定,j=-1,i在[-1,1]之间视不同情况取值.“均分原则”是指在把三元联系数扩展成多元联系数后,最后一个联系分量的系数恒取值-1,而其它联系分量的系数在[-1,1]区间均分取值.例如,四元联系数μ=a+bi+cj+dk中的k=-1,根据“均分原则”i在区间[0,1]取值,j在区间[-1,0]取值(这样区间[-1,1]被均分成2个子区间).又如,五元联系数μ=a+bi+cj+dk+el中的l=-1,i在区间[0.333,1]取值,j在区间[-0.333,0.333]取值,k在区间[-1,-0.333]取值([-1,1]区间被均分成3个子区间),依此方法可知其它情况.根据集对分析原理,联系数中联系分量系数在给定区间内取什么值要按照具体情况具体分析.针对多个评价对象的综合评价排序问题,可约定,上述多元联系数中各联系分量的系数在各自的取值区间取区间中位值,比如,对四元联系数μ=a+bi+cj+dk来说,i=0.5,j=-0.5.这样就可以将综合评价多元联系数μ转化为联系数值.
μ=0.607+0.202i+0.132j+0.059k=0.607+0.202×0.5-0.132×0.5-0.059=0.583
如果有多个被评价对象,则分别计算出各个被评价对象的联系数值.
2.8.2 根据“均分原则”确定“优、良、中、差”的联系数值范围,同时确定评价对象的联系数值所属范围
由于归一化联系数值μ的取值范围只能是[-1,1]区间,用“均分原则”确定“优、良、中、差”的联系数值范围,就是把[-1,1]区间分成4个子区间,[0.5,1],[0,0.5],[-0.5,0],[-1,-0.5],它们分别对应于优、良、中、差4个等级.μ=0.583∈[0.5,1],由此可知,此次实验教学质量综合评价等级为“优”.
如果有多个被评价对象,则可根据联系数值所属范围确定等级后进行优劣排序.当然,也可以直接根据联系数值的大小进行排序.
3 结 论
文章将集对分析方法引入到综合评价实验教学质量中,克服了传统评价方法的单一性和主观性的缺点,同时,此评价模型综合考虑了多种因素对评价结果造成的影响,能充分考虑确定和不确定影响因素.从评价结果来看,集对分析评价模型不仅包含了模糊综合法的特性,而且具有不损失中间信息、评价结果客观可靠的优点,为更客观地进行综合评价提供了新的方法和思路.由于集对分析理论是一门新兴学科,其发展历史较短,因此,该理论将在应用中不断得到完善.
[1] 赵克勤.集对分析及其初步应用[M].杭州:浙江科学技术出版社,2000.
[2] 杨林泉,庄加琳.运用模糊综合评价模型进行实验教学评价[J].统计与决策,2005(5):149-150.
[3] 李辉珍,何天柱,杨成清,等.高校实验教学创新与考核评估实用手册[M].北京:银声音像出版社,2004.
[4] 余国祥.同异反教学评价模型及应用[J].绍兴文理学院学报:自然科学版,1996,17(6):41-48.
[5] 余国祥.综合评价的多元联系数模型及应用.[J].绍兴文理学院学报:自然科学版,2004,24(9):99-102.
[6] 王文圣,金菊良,丁晶,等.水资源系统评价新方法——集对评价法[J].中国科学E辑:技术科学,2009,39(9):1529-1534.
EvaluationofUniversityExperimentalTeachingQualityBasedonSetPairAnalysisModelwithMulti-ElementConnectionNumber
TAO Li-min1,2, XU Zhen-zhen3
(1. Hangzhou Institute of Service Engineering, Hangzhou Normal University, Hangzhou 310012, China; 2. College of Information Engineering, Zhejiang University of Technology, Hangzhou 310023, China; 3. Academy of Art Design, Zhejiang A & F University, Hangzhou 311300, China)
According to the features of experimental teaching, this paper analyzed and ascertained the evaluation index system of experimental teaching quality, set up a new comprehensive evaluation model based on set pair analysis model with multi-element connection number and researched on the evaluation results which are reasonable and reliable by examples, provided a new methods and ideas for comprehensive evaluation of university experimental teaching quality.
multi-element connection number; set pair analysis; experimental teaching; evaluation model
10.3969/j.issn.1674-232X.2011.02.016
2010-10-09
杭州市重点学科项目;浙江省高等教育学会项目(Y200801);杭州师范大学杭州国际服务工程学院2009年教改项目.
陶利民(1975—),男,湖南长沙人,讲师,控制理论与控制工程专业博士研究生,主要从事集对分析理论、服务计算研究.E-mail: tlm5460@163.com
TP301
A
1674-232X(2011)02-0168-06

