函数空间Ck(X)上的T-Tightness和Set-Tightness

杨春梅,李祖泉

(杭州师范大学理学院,浙江 杭州 310036)

函数空间Ck(X)上的T-Tightness和Set-Tightness

杨春梅,李祖泉*

(杭州师范大学理学院,浙江 杭州 310036)

讨论了函数空间Ck(X)在赋予紧开拓扑下的T-tightness和set-tightness性质,利用开k覆盖获得了Ck(X)是T-tightness空间和set-tightness空间的两个对偶定理,将点态收敛拓扑函数空间Cp(X)的相关结论推广到紧开拓扑函数空间Ck(X)上.

函数空间;紧开拓扑;T-tightness;set-tightness;k覆盖

0 引 言

T-tightness空间和set-tightness空间是弱于tightness空间从而弱于第一可数空间的一类拓扑空间.set-tightness空间是由Arhangel’skii A V[1]引入,最初称为拟特征(quasi-character)空间,后来Juhasz I[2]将其称为set-tightness空间,Bella A[3-5]对其进行了系统研究.Juhasz I为了比较set-tightness空间和tightness空间引入T-tightness空间.函数空间Ck(X)的各种类型tightness特征中已经有tightness, fan tightness和可数强fan tightness对偶性的证明,上述性质已推广到集值映射空间Ck(X)[6-7]上.函数空间Cp(X)中的T-tightness和set-tightness性质的刻画是由Sakai M[8]得到的.Ck(X)空间的拓扑性质与Cp(X)有很大区别.McCoy R A, Ntantu I[9]和林寿等[10]对Ck(X)的拓扑性质均有系统的论述.在此给出了具有紧开拓扑函数空间Ck(X)的T-tightness和set-tightness性质与基本空间X的对偶定理,获得了Ck(X)是T-tightness和set-tightness空间的等价性证明.

1 预备知识

在此拓扑空间X是Tychonoff的,λ,τ和κ表示无限基数,ω表示可数序数及基数,cf(κ)表示最小的基数λ使得κ具有一个基数为λ的共尾子集,即cf(κ)=min{λ:|A|=λ<κ,A与κ共尾}.如果κ≥ω,并且cf(κ)=κ,则称κ是正则基数.若κ是正则基数,A⊂κ,|A|<κ,则supA<κ.对于κ≥ω,cf(κ)是正则基数.R表示实直线,Ck(X)为X到R上的所有的连续映射族,并且赋予紧开拓扑.文中未定义的术语和符号均以[10-11]为准.

函数空间Ck(X)上的子基开集形如[K;U]={f∈Ck(X):f(K)⊂U},其中K是X的非空紧子集,U是R中非空开集.

Ck(X)上的基开集形如 [K1,K2,…,Kn;U1,U2,…,Un]={f∈Ck(X):f(Ki)⊂Ui,1≤i≤n},

其中Ki(1≤i≤n)是X的非空紧子集,Ui(1≤i≤n)是R中非空开集.

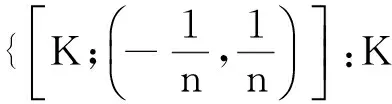
2 函数空间Ck(X)上的T-Tightness

定义1空间X的T-tightness[2]定义为

T(X)=ω+min{τ:cf(κ)>τ,{Fα:α<κ}是X的递增闭集族,那么∪{Fα:α<κ}是X中闭集}.

为了刻画Ck(X)上的T-tightness性质,类似于[8]的T(τ)定义,给出下面的Tk(τ)定义.

定理1对于空间X,下列结论是等价的:

1)T(Ck(X))≤τ; 2)X具有性质Tk(τ).

3 函数空间Ck(X)上的Set-Tightness

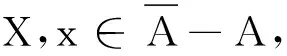
类似于[8]的ts-对和ts(τ)的定义,给出下面的tk-对和tk(τ)定义.

定理2对于空间X,下列结论是等价的:

1)ts(Ck(X))≤τ; 2)X具有性质tk(τ).

[1] Arhangel’skii A V, Isler R, Tironi G. On pesudo radial spaces[J]. Comment Math Univ Caroin,1986,27:137-154.

[2] Juhasz I. Variations on tightness[J]. Studia Sci Math Hungar,1989,24:179-186.

[3] Bella A. On set tightness and T-tightness[J]. Comment Math Univ Caroin,1986,27:805-814.

[4] Bella A. Free sequences in pseudo radial spaces[J]. Comment Math Univ Caroin,1986,27:167-170.

[5] Bella A. A couple of questions concerning cardinal invariants[J]. Questions Answers Gen Topology,1996,14:139-143.

[6] 李祖泉.集值映射空间上的Tightness和Fan Tightness[J].数学研究与评论,2008,28(4):1007-1012.

[7] 郭先一,李祖泉.集值映射空间上可数强Fan Tightness[J].杭州师范大学学报:自然科学版,2010,9(1):23-25.

[8] Sakai M. Variations on tightness in function spaces[J]. Topology Appl,2000,101:273-280.

[9] McCoy R A, Ntantu I. Topological properties of spaces of continuous functions[C]//Lecture Notes in Math.No 1315. Berlin: Springer-Verlag,1988:62-66.

[10] 林寿.度量空间与函数空间的拓扑[M].北京:科学出版社,2004:204-213.

[11] Engelking R. General Topology[M]. Warszwa: Polish Scientific Publishers,1977:87-287.

T-TightnessandSet-TightnessinFunctionSpaceCk(X)

YANG Chun-mei, LI Zu-quan

(College of Science, Hangzhou Normal University, Hangzhou 310036, China)

This paper discussed the T-tightness and set-tightness properties in function spaceCk(X) with compact-open topology obtained two dualities ofCk(X) being T-tightness space and set-tightness space by means of openingk-cover and generalized the related results from point-wise convergence topology spaceCp(X) to compact-open topology spaceCk(X).

function space; compact-open topology; T-tightness; set-tightness;k-cover

10.3969/j.issn.1674-232X.2011.02.007

2010-09-20

杨春梅(1986—),女,吉林松原人,基础数学专业硕士研究生,主要从事一般拓扑学研究.

*通信作者：李祖泉(1963—)，男,吉林怀德人,教授,主要从事一般拓扑学研究.E-mail: hzsdlzq@sina.com

O189.1MSC201054C35

A

1674-232X(2011)02-0124-03