金融超高频数据研究新进展

余德建，吴应宇，周 伟，孟 笋

(东南大学 经管学院，江苏 南京211189)

随着信息技术的迅猛发展，在金融时间序列分析中，人们可以获得股票市场、外汇市场、期货市场实时的每笔成交数据，这样的数据称为超高频数据。超高频数据的时间间隔是不一定相等的，具有时变性。超高频时间序列研究的开创性工作是由诺贝尔经济学奖得主Engle(1998)[1]等人完成的，对超高频数据进行建模与分析，已成为国际、国内的金融学研究热点之一。超高频数据记录的是金融市场的实时的交易数据，这对理解、研究金融市场微观结构具有重要意义。对超高频数据的研究主要从以下两个方面进行，一方面是对交易的到达时间即时间久期进行建模与分析； 另外一方面则是对标值进行建模与分析，标值通常包括交易价格、交易量以及买卖价差等。

一、超高频数据交易时间的研究

关于交易时间的模型主要有两类。一类是由Engle(1998)[1]提出的ACD模型，另一类是由Bauwens和veredas(2004)[2]提出了随机条件持续期SCD模型。

(一) ACD模型

Engle(1998)[1]提出的ACD模型主要分析了交易期间，并假设期间符合随机过程。该模型定义了残差的密度函数以及条件期间的递归函数。ACD模型和GARCH模型具有及其相似的形式，因为GARCH模型是刻画波动率的聚类性的，而ACD模型是刻画持续期的聚类性的。一个滞后阶数是和的ACD模型形式如下：

xi和ψi满足E(xi|xi-1,…,x1)=ψi。 基本的ACD模型假定εi服从指数分布，同时还假定ψi与过去的持续期xi和过去的ψi之间是线性关系。因此，可以从以上两个方面对ACD模型进行改进。

对εi分布的不同假设可以得到不同的ACD模型形式，根据实际情况以及不同的超高频数据特性，对εi分布进行不同的假设至关重要。Engle和Russell (1998)[1]提出了εi服从Weibull分布的WACD模型，此时，xi的分布密度函数为：

其中λ和γ为待估参数。

对ψi与过去的持续期xi和过去的ψi之间关系进行不同的假定，可以得到不同的ACD模型。Bauwens和Goit[5]为了解决基本的ACD模型需要对参数的取值范围加以限制，对参数估计带来不便这一问题提出了LOG-ACD模型，这个模型有两种形式分别是：

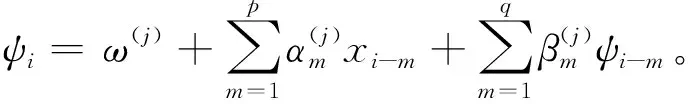
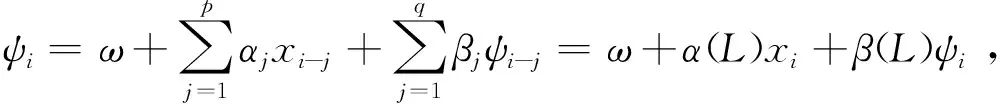
其中，α(L)=α1L+α2L2+…+αpLp，β(L)=β1L+β2L2+…+βpLp。除上述分析的LOG-ACD模型、TACD模型以及FIACD模型以外，常见的ACD模型还有[8]：

以上都是参数形式的ACD模型，形式较多。相对与参数ACD模型而言，对非参数、半参数ACD模型的研究较少。戴丽娜(2009)[9]，徐国祥(2007)[10]关于半参数ACD、非参数ACD模型的进行了研究。戴丽娜(2009)[9]提出了半参数ACD模型并基于模拟样本与调整后的中国股票市场的价格时间间隔样本对模型进行实证分析。与非参数ACD模型相比半参数ACD模型因为在模型中增加了参数部分，因此相对于非参数ACD模型，它增加了模型的解释能力，从参数部分的参数可以看出参数部分对模型究竟有多大影响。徐国祥(2007)[10]引用两步法来测试ACD模型的误差项的分布，第一步包括通过QML估计条件期间过程，以获得误差的一致估计； 第二步衡量基准密度的参数和非参数估计与残差的风险率函数之间的紧密度。

在利用ACD模型对超高频数据交易时间进行研究的另外一个方面就是实证研究。屈文洲(2006)[11]分析了证券市场行情公告牌上提供的信息(存量信息)含量和委托指令流提供的信息(流量信息)含量，并采用ACD模型来检验研究这些信息如何影响我国投资者的行为。通过实证分析，得出ACD模型对投资者行为的解释能力很大，在较长的交易持续期后，紧接着的交易持续期也较长，而在较短的交易持续期后，紧接着的交易持续期就较短，也即出现交易持续期的聚类现象。

郑玉华(2009)[12]利用相邻违约之间的时间间隔数据，对违约传染现象建立了ACD模型，利用该模型对贷款组合中的违约问题进行分析，其研究结果说明了所建立的ACD模型能够很好地反映违约的统计特性，这对于深入了解和研究组合贷款中违约的时间特征以及违约数量的分布状况具有一定的指导作用。

张裕生(2010)[13]利用ACD模型对沪市A股的四只股票的交易持续期进行了实证研究，其研究结果表明交易持续期具有明显的日内模式，并检验log-WACD模型与中国证券市场的吻合程度。

刘向丽(2010)[14]研究了中国期货市场价格久期波动聚类的特征。文章在四种不同残差分布假设下对相应的四种ACD模型进行参数估计，通过检验模型的性能，分析适合我国期货市场的ACD模型及残差的分布，并以此为基础，在模型中加入微观结构因子，据此分析交易量、收益率和持仓量对价格久期的影响。

刘伟(2010)[15]利用Log-ACD模型和一类非参数ACD模型对超高频股票数据交易量久期与价格变化的动态行为进行了研究，研究结果表明在不同的市场格局下，价格变化对交易量的影响会有显著区别。并且阈值的选取会影响交易量久期的统计性质，阈值变大时交易量久期的长记忆性会变弱。

(二) SCD模型

SCD模型比ACD模型具有更优的拟合优度，这点已经被国内外学者证实。SCD模型是一个优秀的久期模型，在SCD模型中，ψi的确定方法与在ACD模型中ψi的是确定方法不一样，SCD模型中的ψi用一个潜在的随机变量来建模。Bauwens(1999)[16]认为该潜在的随机变量具有经济学意义，被认为是用来捕捉市场中的不可观测的信息流。简单的SCD(1,1)模型形式如下[2]：

xi为一个事件在ti-1时刻发生到ti时刻发生的持续期，为建立持续期过程的相依性，对数条件均值设定为服从一平稳的AR(1)过程，这里可以假定ui|Fi-1～N(0,δ2)，εi|Fi-1服从某个带正支撑的分布p(εi)，且两个随机变量之间是相互独立的。其中Ft-1表示过去直到t-1时的信息集。在SCD模型中ui是随机扰动项，因此xi由两个随机变量eψi、εi共同决定。对εi服从的不同概率密度的假定可以得到不同的SCD模型。由于SCD模型中有两个随机变量，使得对其参数估计相当困难，也在一定程度上影响了该模型的发展。

耿克红(2007)[17]比较了ACD模型与SCD模型，指出两类模型均可转化为ARMA模型，具有一定的相通性。并且从实证角度比较了两类模型对持续期序列的拟合优度，其研究结果表明在拟合金融市场超高频持续期数据时，SCD模型比ACD模型更具有优势。耿克红(2008)[18]提出了一种刻画基本SCD模型潜在随机变量的长记忆性的长记忆随机条件持续期(LMSCD)模型。SCD模型的参数估计方法主要有伪极大似然函数估计方法(QML)[2]、广义矩估计方法(GMM)[19]、经验特征函数方法( ECF)[19]、谱极大似然函数法[20]、MCML参数估计方法[21]、马尔可夫链蒙特卡罗参数估计方法(MCMC)[22, 23]，靳珊(2008)[24]将SCD模型转换成非高斯状态空间模型，从而利用非高斯状态空间框架下的Kalman滤波对SCD模型的进行估计。实证结果表明该估计方法的优势为：估计标准差更小，估计更精确。

二、超高频数据标值的研究

交易时间和标值共同构成了超高频数据。ACD模型和SCD模型只是对超高频数据的交易时间建模，然而，根据超高频时间序列的定义，它还包括标值这一重要变量，标值通常包括交易价格(收益率)、交易量以及买卖价差等。目前关于标值的研究主要集中在交易价格(收益率)，价格传递着重要的市场信息，因此，对超高频数据分析时，必须对交易价格或收益率来建模才能充分揭示的微观结构，超高频数据分析中关于交易价格的计量模型有：UHF-GARCH模型和ACD-GARCH模型。

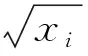
ψi=δiηi,ηi～i.i.d.N(0,1)

上述模型称为超高频广义自回归条件异方差模型，简称为UHF-GARCH模型。徐正国(2005)[26]利用UHF-GARCH模型对上海股市个股及指数的超高频数据进行了实证研究，对上海股市的微观结构中有关交易的时间间隔的聚类性以及时间间隔的长短对投资者行为影响进行了研究。通过研究发现上海股市交易的时间间隔具有很强的聚类性，较长的交易时间间隔表明市场上没有新的信息。

为了刻画超高频金融数据的波动性，Ghysels(1998)[27]提出了ACD-GARCH模型。ACD-GARCH模型的形式如下：

xi=ψiεi,εi～i.i.d.N(0,1)

ri=δiηi,ηi～i.i.d.N(0,1)

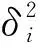
三、超高频数据研究中存在的问题和研究展望

综上所述，近年来对金融超高频数据的研究成果十分丰富，但是也存在一些问题，通过总结、分析已有的问题，对未来超高频数据研究进行展望。

1. 已有实证研究的文献中，研究对象基本是股票，对期货、基金的研究非常少，对期货、基金等金融市场微观结构的深入研究同样具有重要意义，所以未来可以利用超高频数据对期货、基金等金融市场微观结构进行分析。

2. ACD模型、SCD模型都是国外学者研究国外金融市场的微观结构提出来的，因此当把这类模型应用在我国金融市场时，需要考虑我国金融市场的特点。尽管在国外金融市场应用效果很好的模型，也不能直接对我国金融市场进行分析，相应的参数假定、条件期望的函数形式问题需要重新斟酌。而半参数ACD模型、SCD模型对条件期望的函数形式与随机误差项的分布形式要求都没有参数ACD模型、SCD模型强，因此不会因为参数设定不当和函数形式假定不正确而得到错误的结论。因此半参数、非参数的ACD模型； 半参数、非参数的SCD模型是未来的研究方向之一。

3. 相比ACD模型，SCD模型的研究文献较少，究其原因是SCD模型中有两个随机变量，因此参数估计问题很困难。然而国内外学者已经证实SCD模型比ACD模型具有更优的拟合优度，是一个优秀的久期模型。为了对金融市场微观结构更深入的研究、更精确的描述，对SCD类模型深入研究具有重要意义，是未来对超高频数据研究的又一研究方向。

参考文献：

[1] Engle R F. Autoregressive conditional duration: A new model for irregularly-s paced transaction data [J]. Economitrica，1998，66 (5):1127-1162.

[2] Luc Bauwens，David Veredas.The stochastic conditional duration model: a latent variable model for the analysis of financial durations[J] .Journal of Econometrics，2004,119:381-412.

[3] Lunde A.A generalized gamma autoregressive conditional duration model：[Working paper]. Aarlborg University，2000，4-17.

[4] Gramming J，Maurer K O.Non-monotonic hazard function and the autoregressive conditional duration model[J]. The Econometrics Journal，2000，3(1):16-38.

[5] Bauwens L and Giot P. The logarithmic ACD model: an application to the bid-ask quote process of three NYSE stocks [J]. Annals' d'Economie de statistique，2000，60:117-149.

[6] Zhang M.Y.，Russell J. R，Tsay R.S,“A nonlinear autoregressive conditional duration model with application to financial transaction data” [J]. Journal of Econometrics，Vol.104，(2001) ，pp. 179 - 207 .

[7] Jasiak J. Persistence in intergraded durations[R]. York University，Department of Economies，working paper，1999.

[8] 吴武泽. 基于ACD-GARCH模型的股票流动性分析[D]. 对外经济贸易大学博士论文2002.

[9] 戴丽娜. 半参数ACD模型及其在中国股票市场中的应用[J]. 数理统计与管理. 2009(3):318-323

.[10] 徐国祥,金登贵. 基于金融高频数据的ACD模型非参数设定检验[J].统计研究,2007(4):15-18.

[11] 屈文洲. 行情公告牌信息对交易者行为的影响-基于ACD的分析[J].管理世界.2006(11):19-27.

[12] 郑玉华,张涤新. 贷款组合中违约传染的ACD模型[J].中国科技大学学报2009(12) .1272-1276.

[13] 张裕生,王 晶. ACD模型在沪市中的实证研究[J].大学数学2010(4):165-170.

[14] 刘向丽. 中国期货市场价格久期波动聚类特征研究[J]. 管理科学学报2010(5):72-81

[15] 刘伟、陈敏、吴武清. 高频数据交易量久期与价格变化动态行为研究[J]. 数理统计与管理. 2010(5) :518-528.

[16] Bauwens L，Veredas D. The stochastic conditional duration model: a latent factor model for the analysis of financial durations [Z]. CORE Discussion Paper 9958，1999.

[17] 耿克红，张世英.SCD模型与ACD模型比较研究[J].管理学报，2005，5(l)，44-48.

[18] 耿克红，张世英.中国股市超高频持续期序列长记忆性研究[J].山西财经大学学报，2007，29(5)，103-107.

[19] Cathy (qiao) ning. Estimations of the stochastic conditional duration model by the empirical characteristic function method [Z]. Working paper，2004.

[20] 耿克红,张世英.中国股市超高频持续期序列长记忆性研究[J].中国管理科学，2008，16 (2) :7 - 13.

[21] Dingan Feng，Jiang.Stochastic conditional duration models with "leverage effect" for financial transaction [J]. Journal of Financial Econometrics，2004，2 (3):390- 421.

[22] Strickland，Forbes，Martin. Bayesian analysis of the stochastic conditional duration model [J]. Computational Statistics & Data Analysis，2006，50: 2247 -2267.

[23] Chib，S.，Nardari，F. and N. Shephard. Analysis of High Dimensional Multivariate Stochastic Volatility models [Z]. Working Paper，2001.

[24] 靳珊. 状态空间模型对SCD模型的估计[D]. 厦门大学硕士论文，2008.

[25] 徐正国. 上海股市微观结构的超高频数据分析[J].天津大学学报(社会科学版) 2005(5) 161-166.

[26] Ghysels E，Jasiak J，“GARCH for irregularly s paced financial data: The ACD - GARCH models”[J]. Studies in Nonlinear Economics and Econometrics，no. 2 (1998)，pp. 133 - 149.