一类二元时滞神经网络模型同步解的周期性
郭美珍 张 瑗 卢金平
(1.湖南科技学院 计算机系,湖南 永州 425100;2.长沙理工大学 数学与计算科学学院,湖南 长沙 410076;3.湖南大学 数学与计量经济学院,湖南 长沙 410082)
一类二元时滞神经网络模型同步解的周期性
郭美珍1张 瑗2卢金平3
(1.湖南科技学院 计算机系,湖南 永州 425100;2.长沙理工大学 数学与计算科学学院,湖南 长沙 410076;3.湖南大学 数学与计量经济学院,湖南 长沙 410082)
本文对一类二元时滞神经网络模型的同步解进行定性研究,主要是针对网络参数的不同取值,分步地求解一个在一定初始函数空间中给定初始值的泛函微分方程,再讨论模型同步解的周期性。分析表明网络参数在神经网络模型研究中具有极其重要的作用。
神经网络;同步解;时滞;周期性
1 引 言
国际上从20世纪80年代掀起了人工神经网络研究的热潮,至今已经取得了许多优秀的成果,如文献[1-8]。在上述文献中,作者讨论了几类二元时滞神经网络模型(具体模型请参阅所提供的文献)的动力学行为,涉及的内容有周期解、解的收敛性、同步周期轨道的全局吸引性等。
本文将讨论如下二元时滞神经网络模型
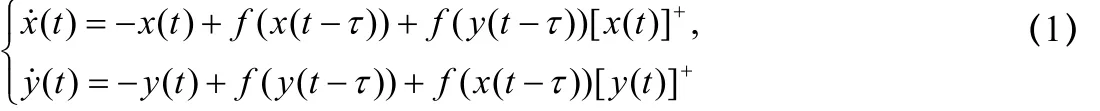
同步解的周期性。这里, )(tx与)(ty分别表示两个神经元的活跃水平;0>为给定常数,表示反馈时滞;),0[:+∞→Rf表示 )(tx 与 )(ty 的信号传输函数;另外,考虑到一个神经元接受另一个神经元的反馈信息的活跃水平的变化还与自身的状态有关,下面还引入了一个函数[ξ]+:R→[0,+∞)。函数 f、 [ξ ]+分别定义如下

其中 > 0为激励常数, 0 < a 设X=C([ − τ,0];R2)为相空间,这是一个由从[−,0]到R2上的连续映射构成的Banach空间, 所赋予的范数为上确界范数。对每个给定的初值 Φ =(ϕ,φ)T∈X (T定义为转置),在区间[0,],[,2],上可以逐个求解系统(1), 得到唯一的映射 ( xΦ,yΦ)T:[−τ,+∞)→R2使得由此便确定了系统(1)在t≥− 上的唯一解(xΦ(t ),yΦ(t))T。对以任意的 Φ =(ϕ,φ)T∈X为初值的系统(1)的解(xΦ(t ),yΦ(t ))T在t≥0时是连续的和t>0时是几乎处处可微的[2]。为了讨论方便, 以下记 ( x(t),y(t))T=(xΦ(t ),yΦ(t ))T表示系统(1)具有初值 Φ =(ϕ,φ)T∈X的解。 在本文中, 将考虑系统(1)的初值 Φ =(ϕ,φ)T在某个 Rij或Rij中且 (0)= (0)的解 ( x(t ),y(t ))T。此时, 对∀t≥0有 x ( t ) ≡ y(t), 称这种解为同步解. 显然同步解可由下列单个方程来描述 本节将讨论系统(1)同步解的周期性, 即讨论系统(2)解的周期性。 定义 若存在某个T>0 和t∗>0 使得系统(1)具有初值Φ的解 ( x ( t ),y(t ))T满足(x(t),y(t))T=(x(t +T),y(t+T))T对任意的 t ≥ t∗成立, 则称 ( x ( t ),y(t ))T为系统(1)的终于T-周期解。 引理[3]对于系统(1), 若 (0 )>0,(0)>0, 则在 [ 0 ,+∞ ) 上恒有 x ( t ) >0, y ( t ) >0。 证明 下面仅证 ∈(b,+∞)的情形, 对于 ∈[a,b]的情形定理的证明类似于 ∈(b,+∞)的情形定理的证明, 故略去。 由于 ∈(b,+∞),故在[0,]上, x(t)满足如下系统 由定理条件及(4)式知:在 [0 ,]上,x ( t)是严格单调递减的, 且有 x (t)=ϕ(0 ) e−t>be−t>0且 (0)>b,lim ϕ (0)e−t=0, t→+∞故必存在一点t1使得x(t1)=b且x(t)>b,∀t∈[0,t1)。 在 [0 ,t + ]上, x ( t)满足系统(3)且有解(4), x( t)是严格单调递减的。解得 1 类似于前面的讨论可知:存在 t2>t1+使得 x ( t ) ∈ [ a,b], ∀ t∈ [t1+,t2]且 x ( t2) =b。 在[t1+ ,t2+]上, x ( t)满足如下系统 且有解 由定 理 条 件及(6)式 知:在 [ t1+ ,t2+]上, x ( t)是 严 格单 调 递 增的, 且 有 x( t ) >b, ∀ t ∈ (t2, t2+]。 解 类似于前面的讨论可知:存在+>23tt使得btx>)(,),(32ttt∈∀且btx=)(3。 在[t2+ ,t3+]上, x ( t )满足系统(3), 且有解 由(7)知:在 [ t2+ ,t3+]上, x ( t)是严格单调递减的,解 对于3tt≥ ,重复上述讨论过程,可以发现)(tx是周期的,且周期为 注记 由于对于],[ba∈(意指对一切]0,[−∈t有],[)(bat∈), 当)(tx严格单调递增进入b>的区域时, 总可以找到某个0*>T, 使得系统(2)的解对],(**τ+∈TTt有btx>)(成立, 这样在讨论系统(2)具有初值],[ba∈或),(+∞∈b的解时, 只需考虑),(+∞∈b的情形即可。 基于定理1及注记, 因此不加证明介绍如下定理 则系统(2)具有初值 的解 )(tx 是终于T-周期的, 且周期 证明 下面仅证),(+∞∈b的情形, 对于],[ba∈的情形定理的证明类似于),(+∞∈b的情形定理的证明, 故略去。 x( t)在 [ 0 ,t1+]上的讨论完全类似于定理1的讨论,这里 即:],[)(batx∈,],[11+∈∀ttt。 类似于定理1的讨论可知:存在 t2>t1+使得 x ( t ) ∈ [ a,b], ∀ t∈ [t1+,t2]且 x ( t2) =b。在[t1+ ,t2+]上, x ( t)满足如下系统 且有解 x (t )= t −t1−τ+ be−τ(9) 由定理条件及(9)式知:在 [t1+ τ , t2+τ]上, x ( t)是严格单调递增的, 且有 x (t ) > b ,∀t∈(t2, t2+]。 解b=x(t2)=t2−t1−τ+ be−τ得 从而由(9)式知: x ( t2+ )=b +。 类似于定理1的讨论可知:存在t3>t2+使得x(t)>b,∀t∈(t2,t3)且x(t3)=b。 在[t2+ ,t3+]上, x ( t)满足系统(3), 且有解 由(10)知:在 [t + ,t+]上, x ( t)是严格单调递减的,解 b =x(t)=(b+τ)e−(t3−t2−τ)得 233 本文讨论了动力系统模型(1)的同步解(即系统(2)的解)的周期性。 证明了在一定初始函数空间X 中给定初值Φ=(ϕ,φ)T使 −a、 −b、 −a和 −b 在[−,0]上不变号, 只要初值(ϕ,φ)T及网络参数 、a、b及 满足一定的条件, 则系统(1)的同步解(即系统(2)的解)是周期的。 本文的结果显示了网络参数 、a、b及 在神经网络模型(1)研究中的重要性。 [1]乔琛,徐宗本.局部域反馈神经网络的全局收敛性[J].应用数学学报,2009,(03):536-545 [2]Wu J H. Introduction to neural dynamics and signal transmission delay[M]. Berlin, New York: Walterde Gruyter,2001,115-138. [3]卢金平,黄立宏.一类二元时滞神经网络模型解的收敛性[J].湖南大学学报,2006,33(6):130-132 [4]Guo S J, Huang L H, Wu J H. Global attractivity of a synchronized periodic orbit in a delayed net-work[J].J.Math.Anal. Appl.,2003, 281 : 620-632. [5]Zhu H Y, Huang L H. Convergence of neural network of two neurons[J]. Journal of Basic Science and Engineering, 2003, 11(2):113-121. [6]Huang L H, Wu J H. Dynamics of inhibitory neural networks with threshold nonlinearity[J]. Fields Institute Communications,2001,29:235-243. [7]Meng Y M, Huang L H. Convergence of solutions of a class of two-neuron bi-threshold neural network model[J]. Fuzzy Systems and Mathematics,2001,15(4):100-104. [8]Meng Y M,Huang L H.Two-neuron bi-threshold neural network dynamical systems with delayed McCulloch-Pitts signal[D].Changsha: College of Mathematics and Econometrics, Hunan University,1999,1-45. TP183;O175.14 A 1673-2219(2011)12-0009-04 2011-01-11 湖南省教育厅资助项目(08C121);湖南科技学院一般项目(09XKYTC008)。 郭美珍(1977-),女,湖南永州人,硕士,讲师,研究方向: 微分方程数值解。 (责任编校:刘志壮)
2. 模型的主要结果

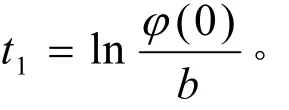

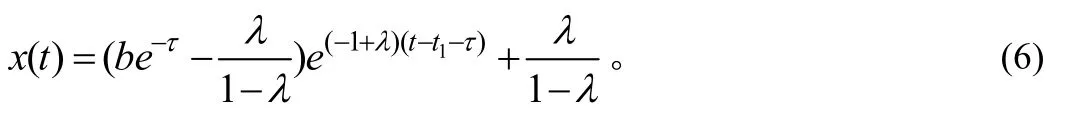
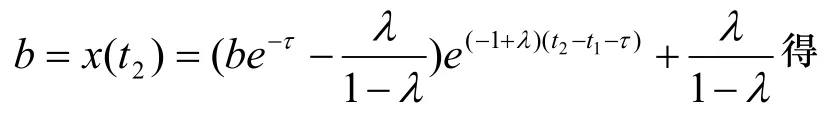

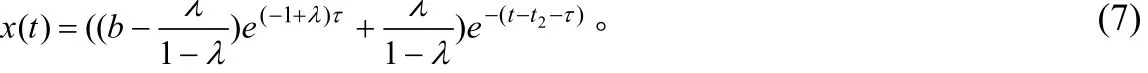
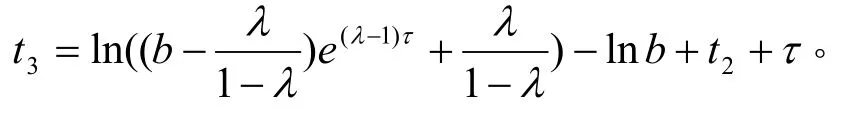





3 结 论

