求解集中载荷下复杂边界条件厚板的挠曲方程

张 丹

（湖南科技学院 数学与计算科学系，湖南 永州 425100）

求解集中载荷下复杂边界条件厚板的挠曲方程

张 丹

（湖南科技学院 数学与计算科学系，湖南 永州 425100）

应用功的互等定理， 得到了两邻边简支另两邻边自由且角点支承的厚矩形板在集中载荷作用下的挠曲面方程；同时, 通过编程计算给出了具有实际价值的数值结果，进一步证明了应用功的互等法求解厚矩形板的正确性和优越性。

功的互等定理法；基本解；挠曲方程；Reissner理论；集中载荷

0 引 言

功的互等法(RTM)是付宝连教授提出的求解板壳力学及弹性力学平衡、稳定和振动问题的一个系统的方法[1-3]。功的互等法求解厚板问题的基本思想是将功的互等定理应用在实际系统和基本系统之间，从而得到实际系统的位移方程，并根据边界条件得到该位移方程得最终解。对于求解厚板弯曲的方法，有叠加法，变分法和有限元法等方法，其中叠加法的应用最广泛，与叠加法比，功的互等法具有求解简单、准确等优点。

本文将功的互等法推广于求解基于Reissner理论的厚矩形板弯曲问题，利用功的互等法研究集中载荷下两邻边简支另两邻边自由且角点支承的厚板的弯曲情况。

1 基本方程

对于Reissner理论[4-5]，控制方程为

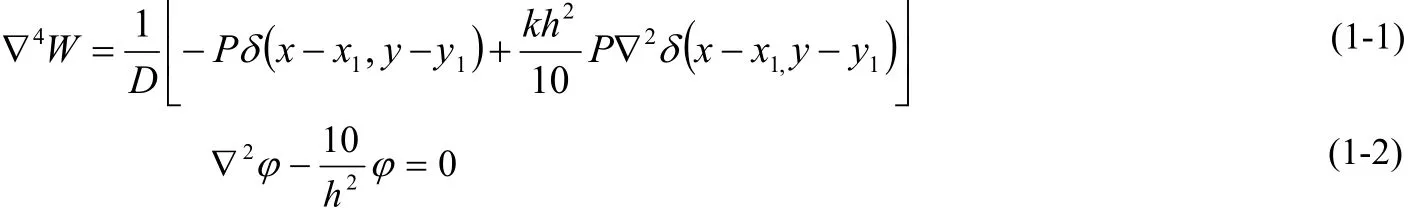
切力，弯矩，扭矩和转角如下：

2 基本解

如图2所示，取只受单位横向二维Dirack-delta函数 (x − , y −)作用的简支矩形板为基本系统，在这种情况下，控制方程(1-1)成为

我们称该基本系统的解为基本解。易知该基本解为

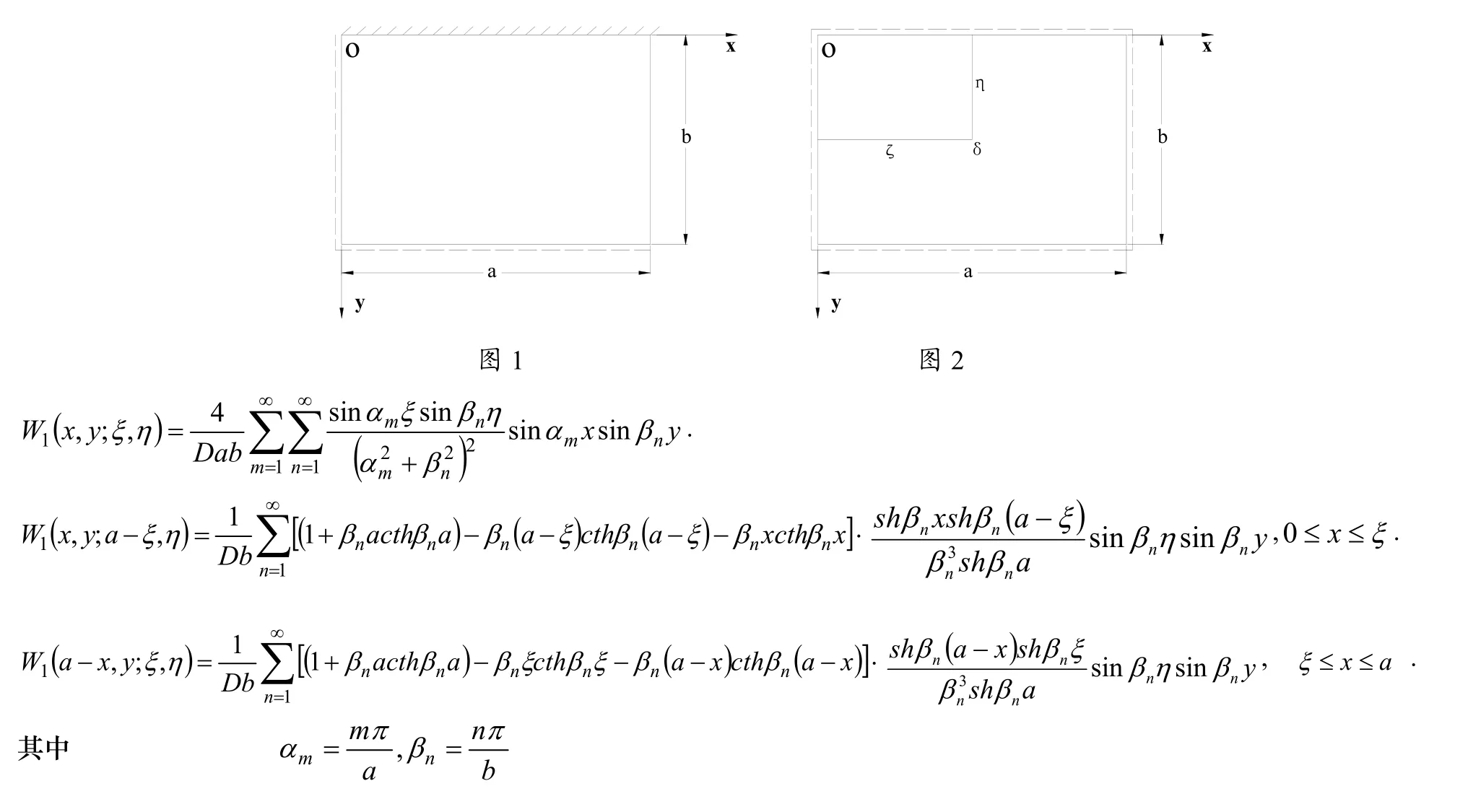
3 两邻边简支另两邻边自由且角点支承的厚矩形板

我们将应用功的互等定理法求解如图3所示在集中载荷 P作用下两邻边简支另两邻边自由且角点支承的厚矩形板的弯曲。

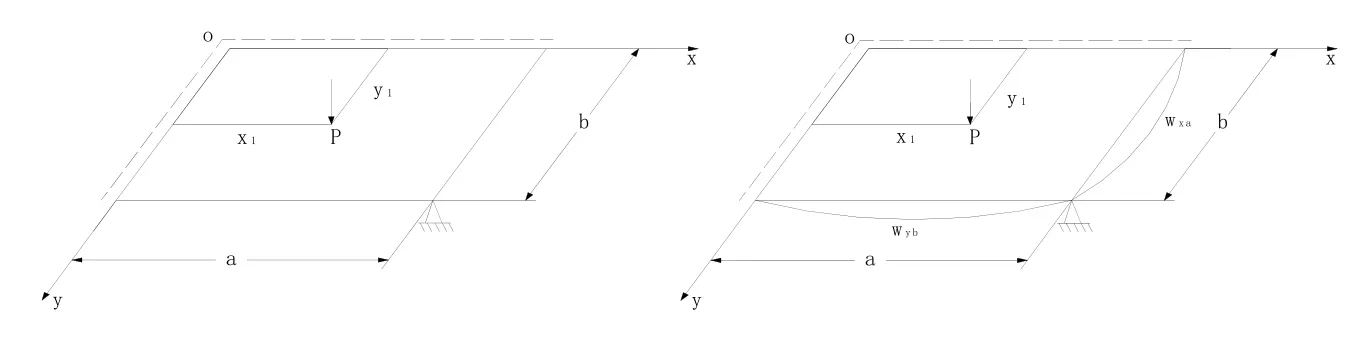
图3 两邻边简支另两邻边自由且角点支承的厚矩形板

如图3所示，以在板面上作用有集中载荷P，两邻边简支另两邻边自由且角点支承的厚矩形板作为实际系统。设

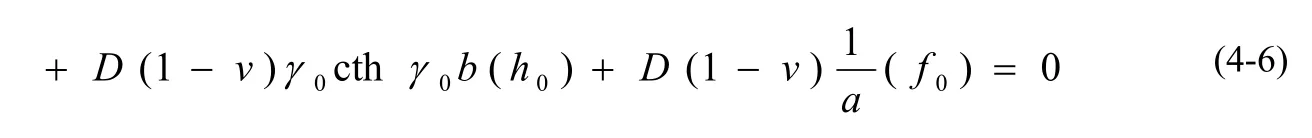
5 算法设计

本例中含有六组未知参数,,,,mnmnhfdb00,hf，其中Λ,3,2,1,=nm，系数矩阵也按对应顺序摆布，先生成分块子矩阵，再组合生成整体系数矩阵，在Matlab中采用选主元LU分解法解边界方程组，取 80, =nm ，结果见表1。

表1 by= 处 )(PW 沿 变化数据表

图4 y b= 处 )(PW 沿 变化曲线

6 数值分析

表1、图4分别给出了在 y = b 2处，挠度沿 变化的数据表和分布曲线，因厚跨比的变化而得到不同的结果。计算中参数分别取 a b =1,E = 3e11P a,v = 0.3,h / a=0.005,0.1,0.2,0.3.以 h / a =0.2为例，与ansys的计算结果比较，两者能够很好拟合；且当厚板中h很小时与薄板挠度的计算结果完全一致。这充分说明了利用功的互等定理求解厚板弯曲问题的正确性及算法选择与程序设计的正确性。

[1]付宝连.弯曲薄板功的互等新理论[M].北京:科学出版社, 2003.

[2]付宝连. 关于求解弹性力学平面问题的功的互等定理法[J]. 应用数学和力学, 1989. 10(5):437-466.

[3]付宝连, 陈英杰. 应用功的互等定理求解中厚板弯曲[J]. 东北重型机械学院学报, 1995.1.13(1):83-90.

[4]苗天德, 程昌钧. 关于弹性板弯曲变形的Reissner理论.

[5]E. Reissner. On the Theory of Bending of Elastic Plates[J]. J. Math. Phys, 1944, 23:184.

A

1673-2219（2011）12-0005-04

2011－10－12

湖南科技学院2009年重点科研课题资助。

张丹（1982－），女，在读博士，数学系讲师，研究方向为有限元数值方法和脉冲微分动力系统。

（责任编校：何俊华）