Fuzzy方阵可实现的条件和性质

岳 芹

(皖西学院数理系，安徽 六安 237012)

Fuzzy方阵可实现的条件和性质

岳 芹

(皖西学院数理系，安徽 六安 237012)

研究了Fuzzy方阵可实现的条件和性质，给出了几种特殊的Fuzzy方阵可实现的条件, 讨论了可实现的Fuzzy方阵的性质。

Fuzzy方阵; 可实现; 条件

模糊矩阵的相关理论在Fuzzy控制、推理和逻辑等领域有着广泛的应用。1982年,刘旺金[1]提出了可实现Fuzzy对称方阵的概念并给出了Fuzzy对称方阵可实现的必要条件。文献[2～4]围绕Fuzzy方阵的可实现问题及其容度作了更深入的探讨。下面，笔者将进一步研究Fuzzy方阵的可实现问题。

1 基本概念

设L为[0,1]格,A=(aij)m×n是L上的m×n阶矩阵,AT表示矩阵A的转置矩阵。用Lm×n表示L上所有m×n阶矩阵组成之集,N+表示正整数之集,n={1,2,…,n}。以下所讨论的矩阵均为[0,1]格上的矩阵, 即Fuzzy矩阵。

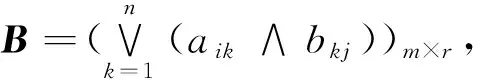
定义2 设A=(aij)m×n,B=(bij)m×n, 令A∪B=(aij∨bij)m×n,称为A与B的并。

定义3 设F=(Fij)n×n,∀k∈N+, 定义:①F1=F；②Fk+1=Fk▯F。

定义4 设F=(Fij)n×n,若F2=F，则称F为幂等矩阵。

定义5 设F=(Fij)n×n, 如果存在P=(Piv)n×l, 使得F=P▯PT, 其中，PT为P的转置矩阵, 则称F对于▯是可实现的, 简称F是可实现的。

定义6 设F是可实现的Fuzzy方阵,记:

ω(F)=min{m|F=A▯AT,A=(aij)n×m}

称ω(F)为F的容度。

2 Fuzzy方阵可实现的条件

设F=(Fij)n×n, 下面讨论F可实现的条件。

定理1 若F是n阶对称幂等矩阵, 则F是可实现的。

证明F为幂等矩阵, 由定义4知F2=F, 即F=F2=F▯F, 又F是对称阵, 所以FT=F, 从而F=F▯F=F▯FT。因此F是可实现的。

定理2 设F是可实现的,则F是n阶对称阵,且Fii≥Fij(i≠j,∀i,j∈n),F2=F。

证明F是可实现的, 由定义知存在矩阵P=(Pis)n×l使得F=P▯PT,从而∀i,j∈n:

显然当i≠j时,Fii≥Fij。又:

所以F是n阶对称阵。

证明因为矩阵A,B均是可实现的, 所以存在矩阵C,D, 使得C▯CT=A,D▯DT=B。令:

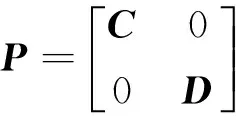
则:

因此F是可实现的。

3 Fuzzy方阵可实现的性质

定理4 若n阶Fuzzy方阵F1,F2是可实现的,则F1∪F2亦可实现,且ω(F1∪F2)≤ω(F1)+ω(F2)。

证明因F1,F2是可实现的,所以存在矩阵P1∈Ln×s,P2∈Ln×t，使得：

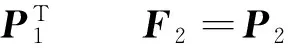
令P=(P1,P2), 则:

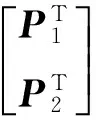
因此F1,F2是可实现的,由定义6即得:

ω(F1∪F2)≤ω(F1)+ω(F2)。

推论1 若n阶Fuzzy方阵F1,F2,…,Ft均是可实现的,则F1∪F2∪…∪Ft亦是可实现的,其中t为正整数。

定理5 设n阶Fuzzy方阵F是可实现的且它的可实现矩阵为P,若P中有2列相同,则可以去掉其中一列。

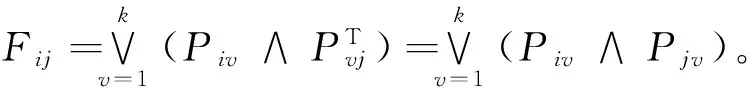
或:

即P中的第s列或第t列可以去掉。

[1]刘旺金. Fuzzy对称方阵的可实现问题[J]. 模糊数学, 1982(1) : 69-76.

[2]Liu Xue-cheng. The least upper bound of content for realizable matrices on lattice [0,1][J]. Fuzzy Sets and Systems, 1996, 80:257-259.

[3]王学平. 如何计算可实现Fuzzy矩阵的容度[J]. 数学年刊:A辑, 1999(6): 701-706.

[4]孔宪明. L-Fuzzy可实现幂等矩阵的秩与容度[J]. 曲阜师范大学学报(自然科学版), 2000,26(4):22-24.

[5]马骥良,于纯海.模糊代数选论[M].北京:学苑出版社,1989:39-100.

[编辑] 洪云飞

10.3969/j.issn.1673-1409.2011.02.002

O159

A

1673-1409(2011)02-0003-02

2010-12-04

安徽省高校青年教师资助项目(2008jq1153)。

岳芹(1978-), 女,2001年大学毕业，硕士， 讲师,现主要从事格论方面的教学与研究工作;E-mail:yqer@163.com。