τ- p变换与偏振分析相结合波场分离方法的研究

张小慧，刘明洋

(地球探测与信息技术教育部重点实验室(成都理工大学)，四川 成都 610059)

王立娟

(四川省安全科学技术研究院，四川 成都 610045)

τ- p变换与偏振分析相结合波场分离方法的研究

张小慧，刘明洋

(地球探测与信息技术教育部重点实验室(成都理工大学)，四川 成都 610059)

王立娟

(四川省安全科学技术研究院，四川 成都 610045)

波场分离是多波多分量地震资料处理的重要环节之一，VSP三分量资料的各种类型的波相互叠加在一起，因此有效地分离出上下行波以及纵横波是VSP资料处理的关键。τ-p变换与偏振分析相结合的波场分离方法能够使地震数据按不同相轴呈点状收敛于不同的区域，用该方法进行VSP波场分离可使能量得到很好收敛，在分离出来的上下波场记录上波形恢复得很好，上下行波、纵横波的相互干扰被完全消除。实际资料处理结果表明，利用该方法分离波场是可行的。

多波多分量；波场分离；τ-p变换；偏振分析

Radon变换[1]在地震同相轴识别、波场分离、压制多次波、速度分析等方面具有良好的应用效果，目前应用用较多的是将反演方法用于改进Radon变换的结果，且无论是线性Radon变换还是双曲和抛物Radon变换，都采用最小平方反演的方法实现，但最小平反演方法的平滑作用会导致Radon域数据存在一定程度的拖尾现象。为此，笔者采取τ-p变换与偏振分析相结合波场分离方法使数据在Radon域以能量团的形式呈现，消除各能量团之间的平滑效应，从而提高Radon域的分辨率，使不同的波场在Radon域更容易分离。

1 τ- p变换方法原理

1.1τ-p变换基本原理

τ-p变换又称线性Radon变换。τ-p变换滤波实际上是按地震波到达的方向和速度的差异对地震波进行分离，不同的p值(或称时距曲线的瞬时斜率)代表了不同的地震波，根据这一特性可达到波场分离的目的[2]。实际工作中，在τ-p域里应用射线参数p值和其在时间轴上的截距τ来描述波的运动学特征。在τ-p域中可以使t-x域中各种交叉在一起的波形各自分离，这为资料处理中分辨各种类型的波带来方便。由t-x域变换到τ-p域相当于做了1次坐标变换，令：

τ=t-px

(1)

式中，p为慢度，其值为速度的倒数;τ为时间轴截距;p的计算公式为：

(2)

图1 下行波的振幅矢量关系示意图

根据波动理论，纵波引起的质点振动方向与波的传播方向一致，横波引起的质点振动与波的传播方向垂直。图1所示为下行波的振幅矢量关系示意图。从图1可以看出，下行纵波的矢量振动集中在第1、3象限，下行横波的矢量振动集中在第2、4象限，即：

(3)

式中，x为水平方向位移；z为垂直方向的位移。

类似地可以得到上行波中纵波和横波的振幅矢量关系：

(4)

用式(3)可把下行波分离成下行纵波和下行横波，用式(4)可把上行波分离成上行纵波和上行横波，以上分离出的各个波型都包括x分量和z分量。根据矢量的旋转合成，能够得到各波型的矢量振幅。τ-p变换的具体过程如下。

1)τ-p正变换 由t-z域变换到τ-p域通常称为倾斜叠加，即：

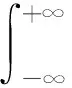
(5)

令t=τ+pz，且上下行波视速度在深度方向上符号相反，即把上行P波定义为负，则下行P波为正。在VSP(垂向地震剖面)记录t-z平面内，任何斜率大于零的直线根据正变换公式叠加，分布在p>0的半平面；斜率小于零的直线则分布在p<0的半平面[3]。于是z-t域中相互重叠混在一起的上下行波经过τ-p变换，上行波分布在p值的负半平面，下行波分布在p值正半平面，因而上下行波场是能够分离的。τ-p正变换的离散形式为：

(6)

式中，tm是时间采样点；pn是tm时刻所对应的慢度；zj是tm时刻所对应的深度。

2)τ-p反变换 将记录空间的地震道变换到τ-p域，进行必要处理后，再将波场反变换到t-z域，就可以恢复分离后的上下行波。令t=τ+pz,得到τ-p反变换公式为：

(7)

将式(7)离散化，可得到τ-p反变换离散公式：

(8)

式中，zn是tm时刻所对应的深度；pj是tm时刻所对应的慢度。

可见，从t-z域中实现τ-p变换并不复杂，但是在变换过程中会出现假频、端点和截断等效应，上述效应会降低变换的质量和精度，导致分离结果的分辨率较差。

1.2τ-p变换与偏振分析相结合法波场分离原理

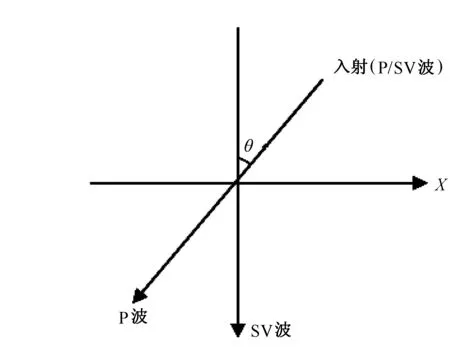
图2 P波与SV波偏振方向示意图

视速度和偏振是地震波的2大特性，τ-p变换法波场分离主要利用了不同波场视速度差异，并考虑地震波的运动学和动力学特征来进行波场分离。用该方法进行纵横波分离时需要进行如下假设[4](井附近的介质是各向同性或者是分层均匀各向同性的)：①质点在震源和井组成的平面内运动，仅由在该平面内传播的P波和SV波所引起。②入射波仅从井的同侧入射。设Ux、Uy、Uz为VSP三分量资料经坐标旋转定向后的3个分量(Ux、Uy为水平分量，Uz为垂向分量)，根据地震波的视速度特性[5]，将1个水平分量Ux(一般选取径向分量)和垂向分量Uz经过τ-p变换得到τ-p域记录Ux和Uz，然后再根据地震波的偏振特性，在τ-p域分离P波和SV波，得到分离后的P波和SV波τ-p谱Up和Usv，最后再将Up和Usv进行τ-p反变换得到分离后的P波和SV波。在τ-p平面内，P波与SV波偏振方向如图2所示。

根据偏振角做矢量合成有：

Uz=Usvsinθsv+UpcosθpUx=Usvcosθsv-Upsinθp

(9)

由式(9)可以推导出：

Up=(Uzsinθsv/Q)-(Uxcosθsv/Q)Usv=(Uzcosθp/Q)-(Uxsinθp/Q)

(10)

式中，Q=sinθpsinθsv+cosθpcosθsv(Q是为简化分母所设)；θp、θsv分别为P波和SV波的入射角：

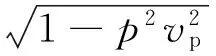
(11)

(12)

式中，vp、vsv分别为P波、SV波速度，m/s。利用上述方法，还可以推导τ-p域内分离后的垂直Z分量和水平H分量的纵横波：

UpH=-Upsinθp=-UZcosθsv·sinθp/Q+UHsinθp·sinθsv/Q

UpZ=Upsinθp=UZcosθsv·cosθp/Q-UHsinθsv·cosθp/Q

UsH=Uscosθsv=UZsinθp·cosθsv/Q+UHcosθp·cosθsv/Q

UsZ=Ussinθsv=UZsinθp·cosθsv/Q+UHcosθp·sinθsv/Q

(13)

式中，UpH、UpZ分别为分开的τ-p域H、Z分量纵波；UsH、UsZ分别为分开的τ-p域H、Z分量横波。

为了验证τ-p变换与偏振分析相结合法进行波场分离的正确性和有效性，模拟了直井垂直分量的上行波场和水平分量定向合成后的上行波场，理论模型分量如图3所示。

3 实例分析

对胜利油田某井VSP单炮3分量资料进行处理。选取其中1炮3分量记录进行3分量定向和波场分离处理。图4(a)所示为Y分量经坐标旋转定向前的记录(简称cr分量),从图4(a)可以看出，剖面的连续性较差，同相轴的能量较弱；图4(b)所示为Y分量经坐标旋转定向后的cr记录,从图4(b)可以看出，剖面连续性和能量都得到了加强，大大提高剖面的质量。图5所示为经坐标旋转定向后上下波场分离的Z分量(简称cv分量)，图6所示为旋转之后的cr分量上下行波分离。从图5和图6 可以看出，用该方法进行VSP波场分离可使能量得到很好收敛，在分离出来的上下波场记录上波形恢复得很好，上下行波、纵横波的相互干扰被完全消除。

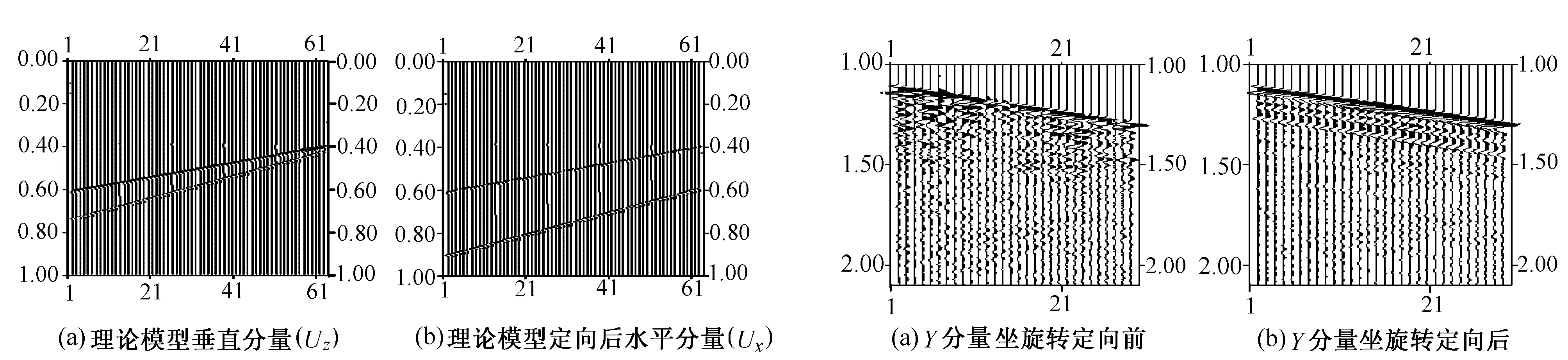
图3 理论模型分量 图4 Y分量坐旋转定向前后cr记录

图5 对cv分量进行上下行波场分离 图6 对cr分量进行上下行波场分离

[1]安鹏，乐友喜.Radon变换波长分离技术研究[D]. 东营：中国石油大学，2009.

[2]曾有良,乐友喜,单启铜，等.基于高分辨率Radon变换的VSP波场分离方法[J].石油物探，2007，46(2)：115-120.

[3]李录明,罗省贤.多波多分量地震勘探原理及方法[M].成都:成都科技大学出社，1997.

[4]王维红，刘洪.抛物Radon变换法近偏移距波场外推[J].地球物理学进展，2005，20(2):289-293.

[5]张玉芬，周建新.影响空间方向滤波效果的因素分析[J].石油与天然气地质，1999，20(3):212-215.

[编辑] 李启栋

10.3969/j.issn.1673-1409.2011.04.013

P631.4

A

1673-1409(2011)04-0042-03