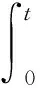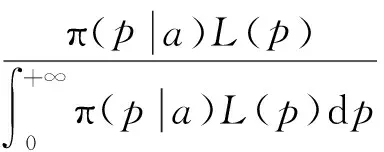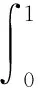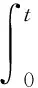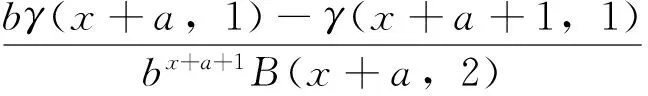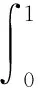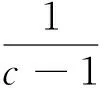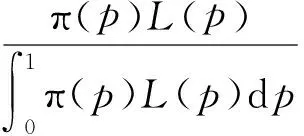复合LINEX对称损失函数下几何分布参数估计
李俊华
(郧阳师范高等专科学校数学系,湖北 十堰 442000)
复合LINEX对称损失函数下几何分布参数估计
李俊华
(郧阳师范高等专科学校数学系,湖北 十堰 442000)
在几何分布可靠度的先验分布为其幂分布时,给出了几何分布可靠度在复合LINEX对称损失函数下的Bayes估计和多层Bayes估计。
几何分布;损失函数; Bayes估计;多层Bayes估计
许多寿命离散型的产品,其寿命服从几何分布,因此对几何分布的可靠性分析具有理论和实际应用价[1,2]。在贝努里实验里,若p为每次实验成功的概率,如果进行了x+1次实验,前x次实验成功且第x+1次不成功(或失败)的概率为:
P(X=x)=px(1-p)x=0,1,2,… 0 (1) 则称随机变量X服从几何分布,其中p为几何分布的可靠度(或成功概率)。 1975年Varian提出了LINEX损失函数[3]: Lb(θ,δ)=e-b(θ-δ)+b(θ-δ)-1 (b>0) 式中,δ为参数θ的估计;b是该损失函数的尺度参数。当b≠0时LINEX损失函数是一类非对称损失函数。文献[4]提出了复合LINEX对称损失函数,表达形式如下: L(θ,δ)=Lb(θ,δ)+L-b(θ,δ)=e-b(θ-δ)+eb(θ-δ)-2 (b>0) (2) 下面,笔者在复合LINEX对称损失函数下给出了几何分布可靠度的多层Bayes估计[5]。 证明在损失函数L(θ,δ)=e-b(p-δ)+eb(p-δ)-2(b>0)下,令δ(x)为p的任一Bayes估计, 则其Bayes风险为R(δ)=E(L(p,δ))=E(E(L(p,δ)|x))。欲使R(δ)最小,只需E(L(p,δ)|x)几乎处处达到最小,由于E(L(p,δ)|x)=E((e-b(p-δ)+eb(p-δ)-2)|x),所以只需证明E((e-b(p-δ)+eb(p-δ)-2)|x)最小,因为δ非负,则最小值不会是0或无穷远点。 记: h(δ)=E((e-b(p-δ)+eb(p-δ)-2)|x)=eb δE(e-bp|x)+e-b δE(ebp|x)-2 对h(δ)关于δ求导并令其为0,即h′(δ)=beb δE(e-bp|x)-be-b δE(ebp|x)=0,解得: 又因为h(δ)关于δ是严格凸函数,故δB(x)是其唯一的极小值点,进而得到Bayes估计是唯一的。 若几何分布可靠度p的先验分布为幂分布,其密度函数为: π(p|a)=apa-1(0 (3) 则此时θ的Bayes估计由以下定理给出。 定理2取式(3)为p的先验分布,在损失函数(2)下,p的Bayes估计为: 证明对几何分布,取p的先验分布为式(3),而p的似然函数为L(p)=px(1-p),根据Bayes定理,p后验密度为: 从而有: 同理可以计算: 所以在复合LINEX对称损失函数下p的Bayes估计为: 引理1在给定的Bayes决策中,对给定的先验分布π(θ),θ的Bayes的δB(x)是唯一的,则它是容许的。 由于几何分布可靠度估计在复合LINEX对称损失函数下是严格凸的,其Bayes估计必是唯一的,由引理可知该估计是可容许的。 (4) 定理3对几何分布,若p的多层先验分布由(4)给出,则在复合LINEX对称损失函数下p的多层Bayes估计为: 证明根据Bayes定理,p的多层后验密度为: 则在复合LINEX对称损失函数下p的多层Bayes估计为: 其中: [1]韩明,崔玉萍.几何分布的可靠度估计[J]. 运筹与管理,2001,10(4):35-38. [2]韩明. 多层先验分布的构造及其应用[J].运筹与管理,1997,6(3):32-40. [3]韦程东,韦师,苏韩. 复合LINEX对称损失下Pareto分布形状参数的E-Bayes估计及应用[J].统计与决策,2009,(17):7-9. [4]张睿. 复合LINEX损失下的参数估计[D].大连:大连理工大学,2007. [5]茆诗松.贝叶斯统计[M].北京:中国统计出版社,1999. [编辑] 洪云飞 10.3969/j.issn.1673-1409.2011.04.004 O213.2 A 1673-1409(2011)04-0011-031 p的Bayes估计
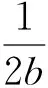
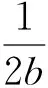
2 p的多层Bayes估计