D.C.乘性规划的全局优化算法
周雪刚
(广东金融学院应用数学系,广东 广州 510521)
D.C.乘性规划的全局优化算法
周雪刚
(广东金融学院应用数学系,广东 广州 510521)
讨论了凸集上的D.C.乘性规划的全局优化算法。首先通过引入辅助变量将D.C.乘性规划问题转化为一个等价的D.C.规划问题;再综合利用分支定界与外逼近方法求解等价问题;最后用一个实例说明算法的实用性。
D.C.乘性规划;全局优化;割平面;锥细分
考虑如下D.C.乘性规划:
(1)
其中,0≤f:Rn→R与0 首先将问题转化为一个等价的D.C.规划,为此,考虑如下函数F(x,λ): (2) 对函数g,h分别定义类似的函数G,H。 定义1设函数f:Rn→R的定义域包含0,且对所有的λ>0与x有f(λx)=λf(x),则f是正齐次函数。 引理1[6]如果f是凸(凹)函数,则当λ>0时,F与是凸(凹)函数。 引理2[7]函数F(x,λ)是正齐次的,且对任意α2>α1>0,当F(x,λ)≠0时,有不等式F(α2(x,λ))=α2F(x,λ)>α1F(x,λ)=F(α1(x,λ))成立。 F(y,β)=βf(y/β)=βf(x)=f(x)g(x)G(y,β)=βg(y/β)=βg(x)=β2 (3) 定义如下D.C.规划问题: (Pd.c.) maxF(y,β) (4) 设问题(P)和问题(Pd.c.)的最优值分别为v,v1,则v≤v1。 定理1如果(y*,β*)是问题(Pd.c.)的最优解,则y*/β*是问题(P)的最优解。如果x*是问题(P)的最优解,则(x*g(x*),g(x*))是问题(Pd.c.)的最优解。 βf(y/β)=F(y,β)≤F(y*,β*)=β*f(y*/β*) (5) 根据引理1可知,问题(Pd.c.)中的函数H是凸函数,而F,G都是D.C.函数。定义函数F1(y,β)=βf1(y/β),F2(y,β)=βf2(y/β),则F1,F2是凸函数,定义G1(y,β)=βg1(y/β),G2(y,β)=βg2(y/β),则G1,G2也是凸函数。则问题(Pd.c.)改写为: (6) 引入辅助变量μ,v,问题(Pd.c.)转化为如下等价的问题: (7) 并且定义如下集合: (8) 由于问题(Pmain)的可行域包含于问题(Pk)的可行域而目标函数相同,则问题(Pk)的最优值是问题(Pmain)最优值的一个上界。假设Tk包含ki个多面体凸锥Cki(i=1,2,…,ki),且都有n+3条以(y0,β0,μ0,v0)为顶点的边,设z0=(y0,β0,μ0,v0)且忽略C的上标,存在n+4个线性独立的点z0,z1,…,zn+3使得: 不失一般性,假设对所有的i=1,2,…,n+3有‖zi‖=1,设θi=sup{θ∈R|z0+θ(zi-z0)∈G2∩G1}和wi=z0+θi(zi-z0)。定义U=(w1-z0,…,wn+3-z0)和L2={z∈Rn+3|z=z0+Uη,eTη≥1},其中η=(η1,…,ηn+3),e=(1,1,…,1)T。由于z0,z1,…,zn+3是线性独立,因而U是非奇异的,且有: L2={z∈Rn+3|eTU-1(z-z0)≥1} 引理3Ω∩C⊆L2∩C。 证明由G2的凸性与L2的定义很容易证明。 设: 引理4Ω∩C⊆(L2∩{z|(z)≤0})∩C。 根据引理3,能求得问题(Pmain)的一个上界,设: u=max{F(y,β)-μ|(y,β,μ,v)∈(L2∩{z|(z)≤0})∩C} 注意到(L2∩{z|l(z)≤0})∩C}是多面体,如果它是非空,则u的值可以它的某个极点上取得,如果它是空,设u=-∞。而(L2∩{z|(z)≤0})∩C}的顶点可以利用文献[9]中的方法求得。对每一个i=1,2,…,n+3,设如果则z0+θi(zi-z0)与都是问题(Pmain)的可行点。那么: 是问题(Pmain)在Ω∩C上一个下界。假设下界是点(yl,βl,μl,vl)上达到,则根据引理2.2可知,不等式F(λyl,λβl,μl,vl)>F(l,βl,μl,vl)关于所有的λ>1都成立。因而: l≥=max{F(λyl,λβl,μl,vl)|(λyl,λβl,μl,vl)∈Ω,λ>1} 大于或者等于l。 3.1算法及收敛性分析 根据前面的讨论,求解问题(Pmain)的算法如下。 步0 设T0是以z0为顶点的满足Ω∈T0的初始锥,置l0=-1,u0=∞,k=0。 步2 如果uk-lk=0,则停止,否则置M={Cki|uki≥lk};选取C∈{Cki|uki=uk},产生一个锥细分集Y。 步3Tk+1=(M/C)∪Y;lk+1=uk,uk+1=uk,k=k+1,转步1。 3.2算例 以下例题说明算法的可行性: 原问题存在3个局部极大解,只有一个全局最优点。对比问题(1)形式,取: 对应的问题(Pmain)的函数为: F1(y,β)-μ=y/4+20β-μF2(y,β)-μ=y2/β-μG1(y,β)-v=y4/(12β3)-v β2+G2(y,β)-v=y2/(2β)+β2-4β-vH(y,β)=y2/β-16β [1]Rúbia M. Oliveira, Paulo A. V. Ferreira. A convex analysis approach for convex multiplicative program-ming[J]. Journal of Global Optimization,2008,41(4): 579-592. [2] Benson H P. An outcome space branch and bound-outer approximation algorithm for convex multiplicative programming[J]. Journal of Global Optim,1999,15: 315-342. [3] Jaumard B, Meyer C, Tuy H.Generalized convex multiplicative programming via quasiconcave minimi-zation[J]. Journal of Global Optim,1997,10:229-256. [4] Konno H, Kuno T, Yajima Y.Global minimization of a generalized convex multiplicative function[J]. Journal of Global Optim,1994,4: 47-62. [5] Benson H P.Global maximization of a generalized concave multiplicative function[J]. Journal of Optimization Theory and Applications,2008,137: 105-120. [6] Rockafellar R T, Wets R J R. Variational Analysis[M]. Berlin : Springer, 1998. [7] Konno H, Yamashita H.Minimizing Sums and Products of Linear Fractional Functions ouer a Poly-tope[J].Naval Research Logistics,1999,46:583-596. [8] Konno H, Ab N.Minimization of the Sum of Three Linear Fractional Functions[J].Journal of Global Optimization, 1999,15:419-432. [9] Horst R,Tuy H. Global Optimization :Deterministic Approaches[M] . 3rd ed. Berlin : Springer Verlag ,1997. [编辑] 洪云飞 10.3969/j.issn.1673-1409.2011.04.001 O221.2 A 1673-1409(2011)04-0001-041 等价问题的转化
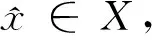
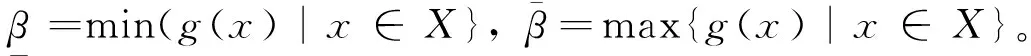
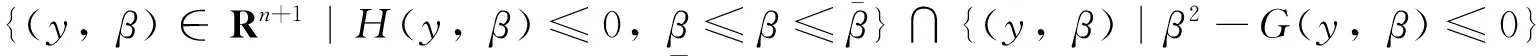
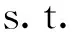
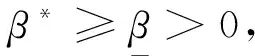
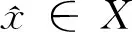
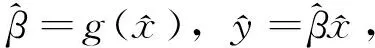
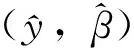
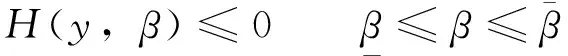
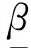
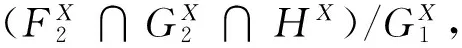
2 上下界
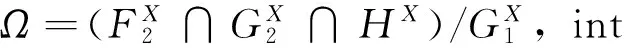
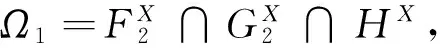
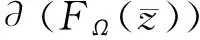
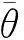
3 算法收敛性及实例