机器人双臂建模与击掌碰撞虚拟样机仿真
严冬明,王斌锐,金英连
(中国计量学院机电工程学院,浙江杭州310018)
与人协作机器人是仿人机器人研究的热点.机器人之间的各个杆件,及机器人与人发生肢体碰撞是研究的难点.刘才山等将系统的动力学方程与并协性约束方程相结合,建立了多点碰撞多刚体系统的碰撞动力学模型[1].刘锦阳等考虑撞击点处的局部变形,基于Hertz撞击模型建立了卫星—太阳帆板柔性系统接触碰撞的动力学模型[2].彼得·艾伯哈特,胡斌以及李敏等通过刚性小球和杆的纵向低速撞击实验验证了Hertz理论模型的正确性[3,4].Pennestri等建立了自由运动的人体手臂的三维动力学模型,并针对肘关节定义了新的运动副[5].Tran Minh Tuan等对已有的仿人机器人肢体运动数据库进行验证,表明应用运动元运动模型可以有效完成人体基本运动动作[6].Park Jung-Jun等设计了非线性弹簧-曲柄滑块机构的关节装置,保证位置精度的同时,更好地完成与人的协作[7-8].由于被动缓冲局限性大,主动缓冲是研究方向,为此需研究系统运动及机构参数对碰撞的影响.已有碰撞理论研究针对理想球-杆碰撞,对典型的碰撞-击掌动作的仿人性,及机构参数对碰撞冲击的影响研究可参考文献少.
本文研究机器人肢体碰撞中动作仿人性及参数对碰撞力的影响及实时仿真平台.首先建立仿人机器人上肢机构[9,10];利用雅克比矩阵建立速度运动学模型;采用拉格朗日能量函数法建立动力学模型;采用非线性等效弹簧阻尼模型建立接触碰撞模型.而后利用 ADAMS软件建立虚拟样机,进行运动学和动力学仿真及动作仿人性分析;针对双手击掌,进行不同刚度下碰撞仿真,分析刚度对碰撞的影响;最后给出了结论.
1 仿人机器人上肢体建模
1.1 上肢体运动学模型
仿人机器人的机构尺寸参照成年人体比例,建模为由大臂、小臂和手组成的三连杆模型.肩关节可前屈/后伸、外展/内收及内/外旋运动,肘关节可前屈/后伸运动,腕关节可内/外旋运动,共5个自由度.本文建立的仿人机器人上肢体各关节作业空间(相对角度)如表1.
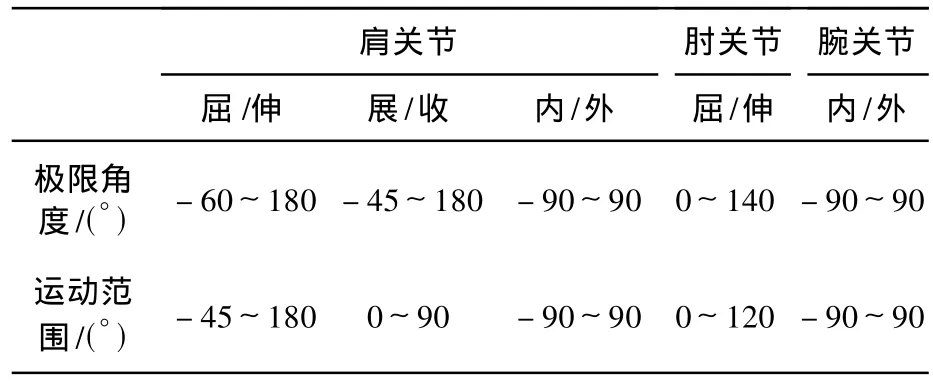
表1 上肢体关节的作业空间Table 1 Rotation range of each joint
本文利用ADAMS,以机器人双手击掌动作为例进行建模.仿人机器人虚拟样机如图1.

图1 机器人上肢虚拟样机Figure 1 Virtual prototype of the humanoid robot upper limbs
机器人与基座之间添加固定副;上臂和躯干之间添加球副;大臂和小臂之间的肘关节以及小臂与手部之间腕关节用旋转副连接[11].模型中左右臂同构,所以数学模型相同.
定义仿人机器人的关节变量阵为
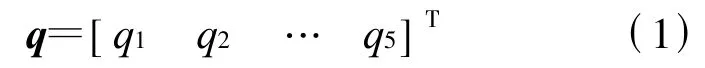
式(1)中:qi为广义坐标,单位:(°).
根据相邻臂齐次坐标变换连乘,可定义机器人手在基坐标系中的位姿为
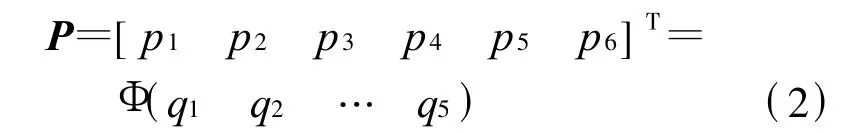
式(2)中:p1-p3表示位置,单位:mm;p4-p6表示姿态,单位:(°),都是广义坐标的函数,Φ为位姿变换函数.
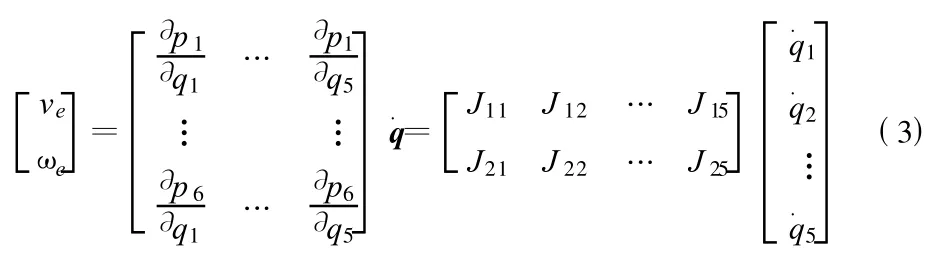
式(3)中,J为雅克比矩阵.
1.2 上肢体动力学模型
拉格朗日能量函数法可以相对简单的方式求解出机器人比较复杂的动力学模型.仿人机器人的拉格朗日方程为
式(4)中:L=U-V,单位:J;U、V分别为上肢体总动能和总势能;τj为关节i的广义力,单位:N.仿人机器人上肢体的势能为
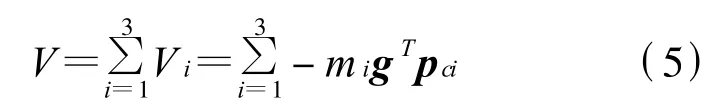
式(5)中:g为重力加速度矢量,mi为连杆i的质量,kg;pci为连杆i质心坐标矢量.
仿人机器人上肢体的动能为
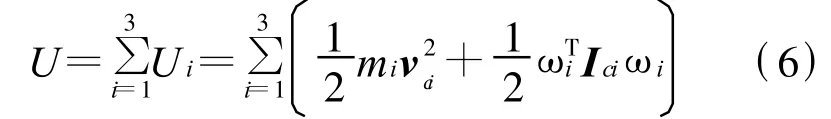
式(6)中:vci为连杆i质心的平移速度矢量,Ici为连杆i质心处的转动惯量矢量,ωi为连杆i的转动速度矢量.
把式(3),(5),(6)代入式(4)求导并写成矩阵形式,可得机器人动力学方程为
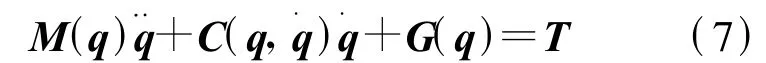
1.3 接触碰撞动力学模型
忽略碰撞点的滑动(切向位移),本文采用接触变形建立接触碰撞动力学方程,利用广义非线性等效弹簧阻尼模型来建立碰撞过程中力和接触变形的本构方程

式(8)中:F为法向接触力,单位:N;k为刚度系数,单位:N·m-1;c为阻尼因子,是接触处几何形状、材料特性、变形量和变形速度的非线性函数;δ为接触面的法向变形量,单位:mm;e为不小于1的指数.
在接触碰撞阶段,肢体从自由运动状态到接触变形状态,产生了运动约束,机构拓扑结构发生变化.本文用约束力来等效运动约束,可将变拓扑结构系统转换为带约束力的无拓扑结构变化系统来处理,所建立的接触碰撞阶段动力学模型为
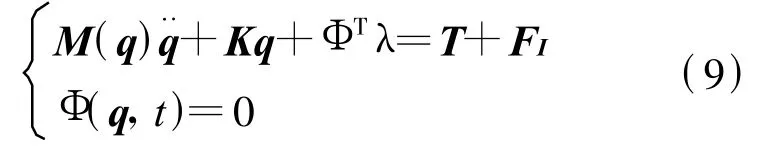
式(9)中:FI为法向接触力F相对于广义坐标q的广义力阵;K为关节刚度阵;Φ(q,t)为接触运动约束;λ为拉氏乘子.
本文采用接触变形模型建立的动力学方程,仿人机器人上肢体自由度与碰撞状态无关.
2 虚拟样机仿真平台
本文所建肢体模型的基本参数如表2.
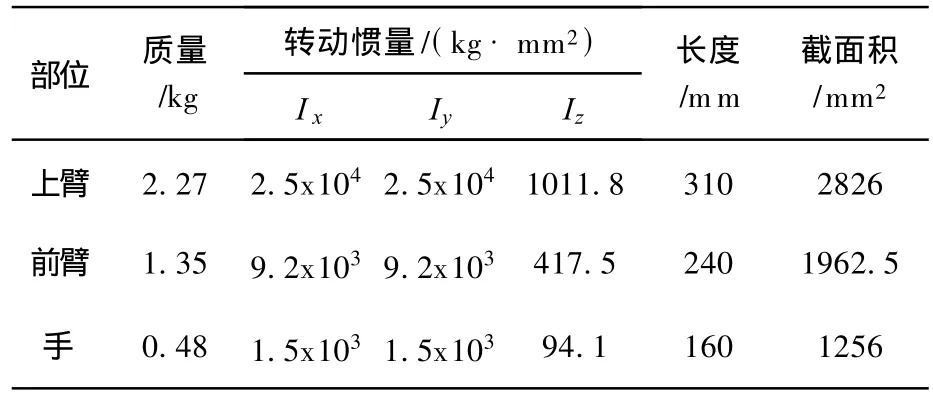
表2 机器人肢体模型的基本参数Table 2 Parameters of the humanoid robot upper limbs
仿真条件:在ADAMS/Solvers模块中设定仿真/时间 1 s,采样频率 200 Hz,计算精度为0.000 1.材料选用的是钢材,密度是 7.8×103kg·m-3,杨氏模量是206 GPa.在仿真过程中,忽略摩擦,机器人只受重力和关节驱动力,积分时间步长足够小,通过对动力学参数和积分器参数的设置,提高求解的稳定性,以保证接触力求解值的收敛.
2.1 运动仿真与分析
将机器人关节相对角度随时间的变化作为输入[13].为实现机器人运动的仿人,本文轨迹规划方法为:通过高速摄像机和人体运动分析软件,获得人体双手击掌动作过程中各个关节的角度曲线;而后用样条曲线来对数据建模.设计0.8 s时双手接触.
各个关节相对角度变化曲线,如图2.
由图2可见,击掌动作是上肢体各关节的复合运动;肩关节的运动最复杂;肘关节的运动量最大;肩、肘关节是人体上肢的主要关节.
上肢体速度,如图3.
由图3可见,仿人运动过程中,各个关节都先是加速运动,而后是减速运动,速度曲线是平滑的,符合缓冲需求.小臂和手运动范围较大,速度较快.三个臂的X轴向的速度峰值都先于Y轴,分析原因为:X轴向运动距离大于Y轴.小臂和手的速度峰值都先于大臂,分析原因为:越靠近碰撞点的肢体,速度峰值越早出现,以便于后续的碰撞缓冲.仿人运动关节角度曲线基本符合正弦曲线形态.
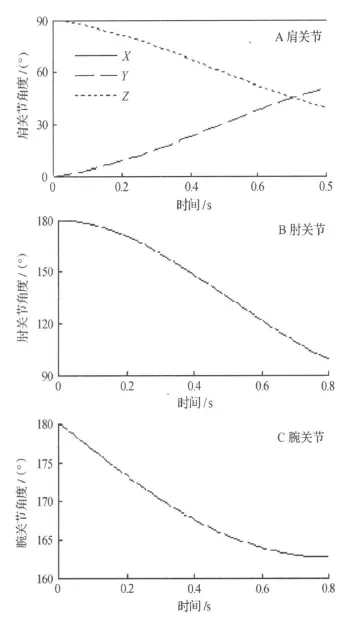
图2 上肢体击掌动作中关节角度曲线Figure 2 Angle curves of joints during handclap
2.2 动力学仿真与分析
通过运动学仿真,可采用ADAMS/VIEW中的测量得到关节运动所需驱动力矩.在建立模型时,各杆件是通过旋转副连接的,所以软件中对模型进行测量的时候,选取旋转副上的力矩值作为测量值.本文将测得的驱动力矩数据输入spline函数中,并用CUBSPL函数将力矩施加到驱动器上,实现仿人击掌动作动力学仿真.各关节所需驱动力矩,如图4.
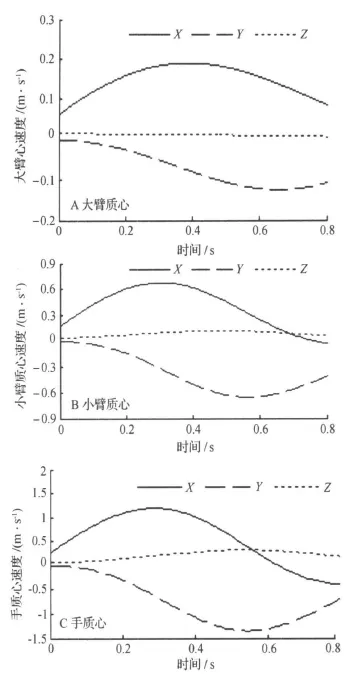
图3 关节笛卡尔空间速度曲线Figure 3 Velocity curves of all parts
由图4可见,肩关节的驱动力矩最大;肩关节前屈/后伸和外展/内收驱动力矩大于内/外旋力矩;肘关节的驱动力比较大;腕关节的驱动力矩比较小.0~0.6 s是加速驱动阶段;在0.6 s左右,关节力矩开始为击掌缓冲而变化.击掌前的缓冲过程为:肩、肘关节驱动力矩逐渐减小,腕关节驱动力矩逐渐变大,但三个关节驱动力矩绝对值的大小关系不变.值得注意的是,距离碰撞点最远的肩关节驱动力矩下降为负值,分析原因为:肩关节和肘关节的驱动力矩方向不同,便于更大范围、更快速实现碰撞点速度调节;同时肩关节反向力矩使得双手碰撞后快速反向运动离开.
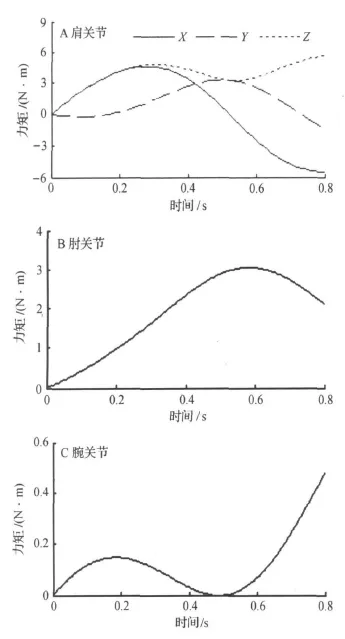
图4 各关节驱动力矩Figure 4 Torque of joints during handclap
2.3 碰撞仿真与分析
在ADAMS中,采用IMPACT函数来实现上述接触力模型.机器人手臂材料采用钢材,当接触力没有超过极限值时,接触可近似定义为刚性碰撞形式.本文在ADAMS中定义双手之间的接触类型为contact,定义k为3.86×108N·m-1,e为1.1,c为10,接触面的法向变形量δ的最大变形值为0.01 mm.
定义法向接触力F作用在各个关节处的力矩为碰撞力矩,可通过雅克比矩阵与F的相乘得到.其变化曲线,如图 5.
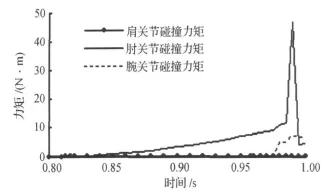
图5 击掌碰撞力矩影响变化曲线Figure 5 Experimental results during dynamic handclap
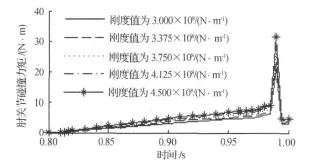
图6 肘关节碰撞力矩局部放大Figure 6 Various stiffness experiments during handclap
从图5可见,在击掌碰撞下,肘关节受到的力矩影响最为明显;肩关节受到的力矩为零(由于肩关节转动中心轴线与接触面法线相交);腕关节受到的力矩并不是最大.由于碰撞变形(即接触面的法向变形)需要一定时间,所以各关节所受碰撞力矩的最大响应出现在两杆接触后约0.17 s时.两杆接触时是指两杆的中心轴线间的距离等于两杆的半径之和时.由于采用了广义非线性等效弹簧阻尼接触力模型,各关节碰撞力矩达到峰值后,在被动缓冲下,各关节所受的力矩迅速下降.
碰撞缓冲后,腕关节所受的力矩大于肘关节.当击掌动作完成后,受到接触力作用,上肢体间存在着相互离开的运动.由于手离碰撞点距离最近,在完成了击掌动作后以及下一次再击掌,腕关节带动手运动范围较大,所以腕关节上力矩较大.
利用ADAMS的参数化设计功能,将IMPACT函数中刚度系数k定义为一个设计变量,取值范围为3.0×108N ·m-1~4.5×108N ·m-1,在其变化区间内均匀地取指定的几个值.运行一次ADAMS中的设计研究(Design Study),步长为0.375×108N·m-1.在不同的接触刚度下,肘关节受到碰撞力矩和接触刚度值之间的关系,如图6.
由图6可见,接触刚度值越大,碰撞力矩越大,刚度系数与力矩最大值之间的函数关系基本表现为线性关系.实验发现,不同接触刚度下,肘关节受到的力矩都最明显.
3 结 语
碰撞是时变的动态过程,时间短,计算复杂.通过本文的建模和仿真分析,可得:
1)建立的仿人机器人肢体碰撞实验平台可方便实现仿人运动轨迹和碰撞参数的测量,为关节驱动器的设计和选型提供基础;
2)在击掌碰撞前,各关节的角速度都是先增速后减速,基本呈现出正弦曲线形态,所以机器人关节速度的仿人运动规划可采用正弦插值法,且峰值的相位关系是动作拟人化的关键;
3)在击掌碰撞中,肘关节所受碰撞力矩最大;被动缓冲后(到两手臂分离前),腕关节所受的碰撞力矩最大;
4)碰撞参数对碰撞有重要影响,尤其是刚度系数,基本与接触力和碰撞力矩成线性正比关系.
本文仿真方法所得机器人动作仿人性好.利用虚拟样机仿真平台可研究碰撞,且成本低.下一步将柔性体引入肢体,同时添加柔性关节,研究接触力和柔性体模态之间的关系.
[1]刘才山,陈 滨,彭 翰,等.多体系统多点碰撞接触问题的数值求解方法[J].动力学与控制学,2003,1(1):59-65.
[2]刘锦阳,洪嘉振.卫星太阳电池阵的刚-柔耦合动力学[J].空间科学学报,2004,24(5):367-372.
[3]彼得·艾伯哈特,胡 斌.现代接触动力学[M].南京:东南大学出版社,2003:77-91.
[4]李 敏,诸德超.球杆碰撞问题的数值分析和实验研究[J].北京航空航天大学学报,2001,27(1):62-65.
[5]PENNESTR E,RENZIA,SANTONOCITOP.Dynamic modeling of the human arm with video-based experimental analysis[J].Multibody Sy stem Dy namics,2002(7):389-406.
[6]T RANM T,PHILIPPE S,MICHEL T.Humanoid human-like reaching control based on movement primitives[C]//International Symposium on Robot and Human Interactive Communication.Italy:IEEE,2010:546-551.
[7]KIMHS,SONG JB.Safe Robot A rm with Safe Joint M echanism using Nonlinear Spring System for Collision Safety[C]//Proceedings of the IEEE International Conference on Robotics and Automation.Kobe:IEEE,2009:3371-3376.
[8]PARK J J,SONG J B.Safe Joint Mechanism using Inclined Link with Springs for Collision Safety and Positioning Accuracy of a Robot Arm[C]//Proceedings.of the IEEE International Conference on Robotics and Automation.USA:IEEE,2010:813-818.
[9]金英连,程 峰,郑成伟,等.智能写字机器人机构与递阶控制系统设计[J].中国计量学院学报,2009,20(3):249-253.
[10]郭丙华,胡跃明.三连杆移动机械臂模型与运动规划[J].控制理论与应用,2005,22(6):965-968.
[11]王学影,岩君芳,叶树亮,等.关节臂式坐标测量系统关键技术研究[J].中国计量学院学报,2010,21(1):12-15.
[12]王斌锐,傅 莉,谢华龙,等.多轴含闭链智能仿生腿摆动相建模与控制[C].中国控制与决策学术年会.哈尔滨:东北大学出版社,2005:612-615.
[13]梁喜凤.室内地面清洁机器人路径规划[J].中国计量学院学报,2006,17(1):64-68.

