一种基于GA的聚类集成算法
何灵敏,潘益民
(中国计量学院信息工程学院,浙江杭州310018)
聚类是一种科学研究中经常要用到的技术,是认知未知事物的重要手段,也一直是机器学习领域中一个活跃的研究方向.现有的聚类方法有不下数百个,但都只适用于解决特定问题.寻找泛化性能好的聚类算法一直是研究者的一个努力目标.2000年左右,人们发现通过集成多个聚类结果,可构造出一个集成的聚类结果.新构造的聚类结果相比于原来单个聚类结果有更好的平均性能,且适用于处理多种问题.此后,聚类集成开始成为聚类研究的一个新方向.Topchy A.在他的论文[1]中将聚类集成的优点概括为:鲁棒性、适用性、稳定性、并行性和可扩展性.
聚类集成的思想主要是利用普通聚类算法生成的多个聚类结果,来构造出一个更加优秀的结果.每个聚类集成算法都由以下两个部分组成:基聚类算法和一致性函数(也称为共识函数).基聚类算法用于对同一个待聚类数据产生多个聚类结果.这些产生的聚类结果所组成的集合被称为一个聚类集体.一致性函数是指用于从产生的聚类集体中得到一个最终聚类结果的算法.聚类集成算法的一般过程是先由基聚类算法产生一个聚类集体,然后使用一致性函数从聚类集体中计算出一个集成聚类结果.
近年来,聚类集成技术的研究取得了很多成果.按照文献[2]的分类方法,现有的聚类集成算法大致可分为以下五类:(1)基于互联合矩阵的方法;(2)基于互信息理论的方法;(3)基于图形划分问题的方法;(4)基于有限混合模型的方法;(5)基于投票的方法.这些方法从不同的角度入手,解决了如何产生一个集成聚类结果的问题.但是这些方法都存在着各自的局限性.
总结前人研究的经验和成果,本文提出一种基于GA(genetic algorithm)的集成算法(ECUNGA).该算法本质上属于基于互信息理论的方法,使用平均互信息(normal mutual information,NMI)表示两个聚类结果之间的相似度,以GA作为共识函数,搜索一个与聚类集体差异度最小的聚类.我们借用了成熟的GA算法搜索集成聚类结果,使算法不易陷入局部解,并在UCI数据进行试验,取得了良好的效果.
1 基聚类算法
目前常用的基聚类算法有很多,按照产生聚类差异性方法的不同,可以分成以下几类[3]:(1)使用不同算法生成聚类集体;(2)使用同一算法不同参数生成聚类集体;(3)使用不同数据子集生成聚类集体;(4)使用不同特征子集生成聚类集体.
我们的基聚类算法采用经典k-means方法,即通过随机确定k-means算法的初始点,运行多次算法,得到所需要的聚类集体.采用k-means算法的优点是算法简单、运行速度快.在实验中与k-means算法进行比较,可以证明集成算法的有效性.
2 一致性函数
一致性函数是本算法设计的重点,设计的核心思想是利用GA搜索一个与聚类集体最统一的聚类结果.统一度则由到聚类集体中每个聚类的NMI值之和定义.其中NMI的定义形式如下:
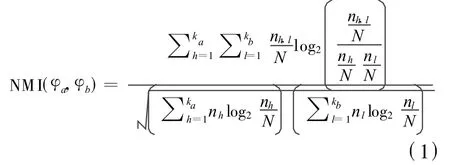
其中ka和kb是聚类φa和φb中类的个数;nh,l是同时在φa的h类中和φb的l类中点的个数;nh是在 φa的h类中点的个数;nl是在φb的l类中点的个数.NMI的值介于0到1之间.
一致性函数的算法结构描述如下:
Begin
Step 1.firstTime=true;
Step 2.t=0;if(firstTime=true)执行初始化种群方法1得到P(t);转到Step 4;
Step 3.执行做初始化种群方法2得到P(t);
Step 4.计算种群P(t)中元素的适应度;令t=t+1;
Step 5.判断是否满足停止条件,如果满足则停止并转到step 9;
Step 6.根据计算的适应度,从种群P(t-1)中选择个体进行交叉操作;
Step 7.随机从种群P(t-1)中选择少量个体进行变异操作;
Step 8.用新产生的个体组成新种群P(t);转到Step 2;
Step 9.记录最好的个体和适应度值;
Step 10.if(firstTime==true)time=false;转到Step 1;
Step 11.比较得到的所有最好个体,选择一个适应度最高的个体输出;停止.End
从算法结构可以看出,我们的一致性函数主体是具有两个初始种群产生方法的GA算法.下面从GA算法的各个部分进行具体描述:
为了表达的方便,先对下面需要用到的符号进行定义:D表示待聚类数据总体,m表示D中的数据点的个数,Di表示第i个数据.C表示D的一个聚类结果,k表示C中的聚类个数,Cj表示C中第j个聚类.R表示基聚类算法得到的聚类集体.
1)编码与解码
个体编码形式如下:
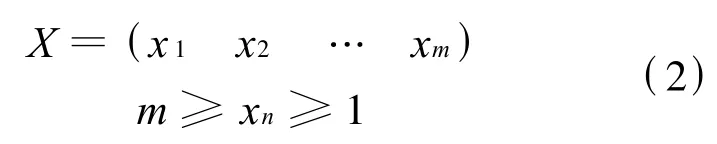
xn的取值表示该数据点属于的聚类.如xi=j,就表示Di属于Cj.
2)初始种群产生
算法使用的初始种群产生方法共有两个,分别用在两次单个遗传算法中.两个方法都可以描述如下:
算法都使用已经用其他单个算法得到的聚类结果集R作为产生初始种群的基础,采用有放回的抽样技术从R中抽样出n个聚类结果,其中,n是设定的初始种群的大小.然后我们再对抽样出的聚类结构进行随机化处理,即在每个聚类结果中随机选出s%的数据进行随机赋值.s被称为初始化随机参数,它的取值会影响收敛速度和搜索全局解的能力.
对于种群产生方法1,s的取值为0.
对于种群产生方法2,s的取值根据问题不同自定义,一般取20左右.
3)适应度函数
我们用个体到其他个体的NMI值之和作为适应度函数,形式如下:
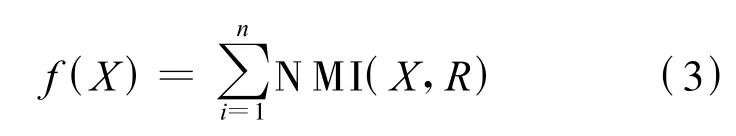
其中,n是设定的初始种群的大小,Xi表示种群中第i个个体,Rj表示R中第j个聚类结果.
4)交叉操作
交叉操作是设计聚类集成算法的难点,因为各个聚类结果中的相同标签值都有可能表示不同含义,所以不能采用普通的单点交叉或多点交叉.我们设计的交叉操作,如图1.
5)变异操作
采用单点变异法,即选择一个变异点,随机产生一个随机聚类标签进行替换.
6)GA搜索停止条件
GA搜索停止条件共有两个,满足任意一个条件,GA搜索将停止.条件一是GA搜索超过了设定的最大允许代数.条件二是GA搜索最大停滞代数达到最大允许值.
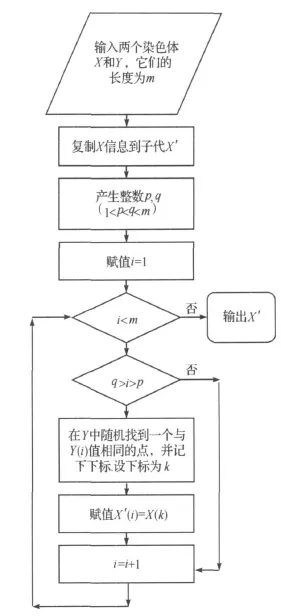
图1 交叉操作流程图Figure 1 Flow chart of crossover
3 实验与结果分析
为了说明ECUNGA算法的有效性,我们使用UCI数据集在MATLAB 7.0环境下进行实验.
3.1 数据集
实验使用选自 UCI数据集的5个数据集进行实验,所选的数据集都为完整的数值型数据集.详细信息,如表1.
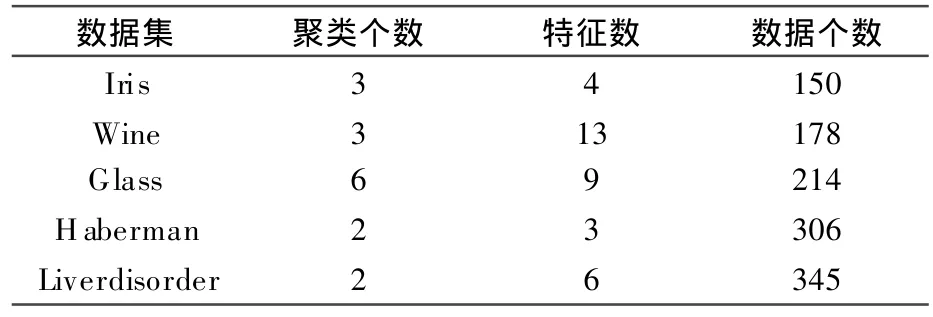
表1 实验数据集描述Table 1 Description of experimental data sets
3.2 实验结果分析
实验采用正确率作为衡量算法的标准.为了分别说明算法的有效性和对聚类集体数量对算法的影响力,实验分为两部分进行.
3.2.1 算法有效性实验 在本实验中算法ECUNGA的聚类集体的大小设置为40,种群产生方法2的初始化随机参数为20,GA最大允许代数为500,最大允许停滞代数为50.使用ECUNGA算法得到的聚类结果与使用k-means算法得到的聚类结果进行比较.以10次计算的平均正确率做比较,结果如表2.
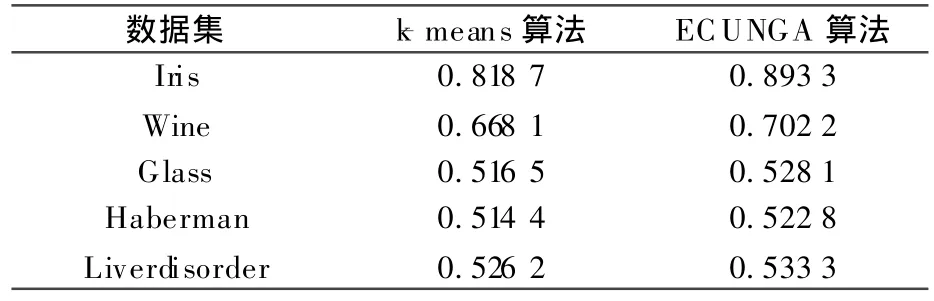
表2 有效性实验结果Table 2 Experimental result
从实验结果可以发现,在以上5组数据上,ECUNGA算法计算的正确率都高于简单k-means算法计算的正确率.这表明ECUNGA可以有效的集成聚类集体的有用信息,构造出更加优秀的聚类结果.
3.2.2 聚类集体规模对算法影响力的实验 在本实验中算法ECUNGA的聚类集体的大小分别设置为 5、10、20、40,其它参数设置同上.实验在Iris、Wine和Glass数据集上进行,比较结果的10次平均正确率在不同规模聚类集体下的差异,其结果如表3.
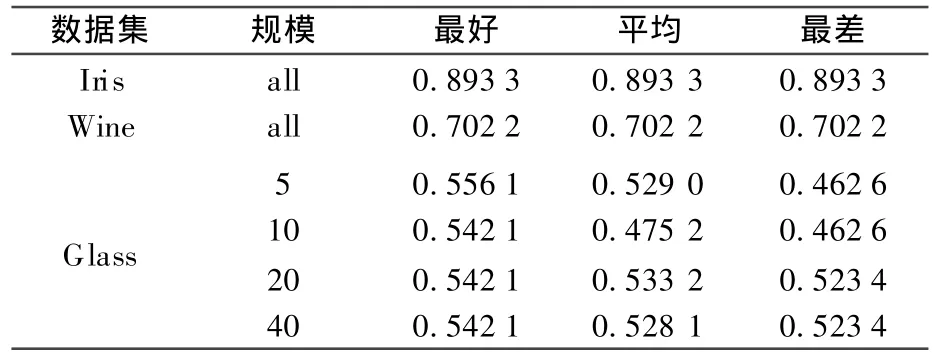
表3 聚类集体规模对算法影响力实验结果Table 3 Result of collective size influence on clustering algorithm experiment
从实验中可以发现算法在数据集Iris和Wine上对聚类集体的规模不敏感,而在Glass数据集上聚类集体的规模小于20时算法不是很稳定,最好和最坏结果相差比较大.所以算法在使用时,应产生规模在20以上的聚类集体,以保证算法稳定性.
4 结 语
本文提出了一种基于GA的聚类集成算法(ECUNGA).算法使用k-means的固有随机性,产生一个聚类集体.使用特别构造的GA算法搜索一个到聚类集体平均NMI值最小的结果作为最终聚类.算法在UCI数据集上进行实验,取得了满意的结果,证明了算法的有效性.
[1]TOPCHY A,JAIN A K,PUNCH W.A Mixture Model for Clustering Ensembles[C]∥Proceedings of the 4th SIAM International Conference on Data Mining.Florida:SIAM,2004:379-390.
[2]阳琳赟,王文渊.聚类融合方法综述[J].计算机应用研究,2005(12):8-11.
[3]罗会兰,孔繁胜.聚类集成关键技术研究[D].杭州:浙江大学,2007.
[4]陈秋灵,徐江峰.用遗传算法搜索一维光子晶体带隙[J].中国计量学院学报,2007,18(1):70-74.
[5]李彬,张化祥.基于Bugging的聚类集成方法[J].计算机工程与设计,2010,31(1):164-166.
[6]GELBARD R,GO LDM AN O,SPIEG LER I.Investigating diversity of clustering methods[J].an Empirical Comparison Data&Knowledge Engineering,2007,63(1):155-166.
[7]李 科,田社平,王志斌.遗传算法加权中值滤波器的优化设计[J].中国计量学院学报,2008,19(1):56-60.
[8]张晓菲,张火明.精英策略的改进非支配遗传算法[J].中国计量学院学报,2010,21(1):52-58.
[9]杨 燕,靳 蕃,KAMEL M ohamed.聚类有效性评价综述[J].计算机应用研究,2008,25(6):1630-1638.
[10]李 凯,常圣领,高 悦.基于聚类技术的集成学习算法研究[J].河北大学学报:自然科学版,2009,29(2):209-213.

