SPLASH诺模图的修正及应用
蒋 娟,张火明
(中国计量学院计量测试工程学院,浙江杭州310018)
风暴潮是指由于强烈的大气扰动,如强风和气压骤变所引起的海面异常升高或下降的现象[1],也是通常所说的风暴增水或风暴减水.我国是严重的风暴潮受灾国家,一次风暴潮的袭击将造成巨大的经济损失并给人类生命和财产带来极大的威胁,其社会影响不可估量.我国改革开放以来,随着滨海城乡工农业的快速发展、社会经济建设的不断繁荣和沿海基础建设的迅速增加,相同条件的风暴潮灾的直接、间接损失已呈逐年加重的趋势[2].因而,加强风暴潮理论和数值模拟研究十分迫切.
1954年,H.Kivisild用手算对美国 Okeechobee湖作了最早的风暴潮数值预报[3],1956年,德国的Hansen第一次将计算机用于风暴潮数值模拟,之后很多国家都相继提出了各种风暴潮预报模式,为世界风暴潮数值模拟研究的发展做了巨大贡献.
SPLASH模式即Special Program to List Amplitudes of Surge from Hurricane的缩写形式,是1972年由美国Jelesnianski所研制的动力数值风暴潮预报模式.该模式通过查算3张预先做好的诺模图来确定开阔海岸登陆台风的最大增水值.诺模图方法是靠数值产品建立起来的,用以查算风暴潮特征值及其空间分布.这类方法查算简便、精度高,至今仍在国内外一些国家的实时预报中被采用,对防潮工程、港工建筑极值水位的设计也有实用价值.
在查阅了文献的基础上,我们发现了SPLASH模式诺模图中的一些问题,特在本文中对其作出修正与完善,希望能对风暴潮的预报提供一些参考.
1 SPLASH模式诺模图的建立
1.1 SPLASH模式诺模图的建立
影响风暴潮成长的参数很多,主要有气压示度(ΔP)、矢量风暴运动、最大风速半径(R)、登陆点附近的离岸海底地形以及纬度.为了预报风暴潮的最大增水并实现这一客观预报技术,动力模式是一种有效的计算模式,它可以通过一次改变一个参数且保持其它参数不变来计算最大增水[4].
在该模式的计算中,气压示度起主要作用,最大风速半径起次要作用.为了得到计算最大增水初估值SP的第一张诺模图,对风暴潮运动的“标准水域”和“标准风暴运动”作了规定,图中相关曲线正是以此为前提计算的.标准水域,即水域有一条直的海岸线,在水域中,向海方向的深度廓线是一维的,海岸的水深是4.5 m,其坡度约为0.5 m/km,如图1.标准风暴运动,是指风暴具有7 m/s的移速由海向陆地正交地移动[5,6].标准风暴运动可以视为各登陆风暴假想的平均风暴运动.
先假定风暴具有同样的最大风速半径R(km),且所有风暴都在北纬30°登陆.只改变ΔP值,得到一条曲线,第二步对同样的风暴进行计算,只改变R,从而绘制出对应不同的R,最大增水SP相对于ΔP的诺模图,如图2.知道ΔP和R,查图2,即可获得SP值.图中每一条线几乎都是通过坐标原点的一条直线,这意味着所预报的风暴潮都有一个相对误差δ P/ΔP,δ P为气压示度的变差.例如,当气压示度 ΔP为100 hPa时,若其中变差量δ P为1 hPa,则引起的ΔP作极大风暴潮高度估报值的误差为1%,这完全能满足气压示度精度的要求.
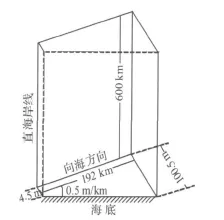
图1 标准水域(长600 km,宽192 km)Figure 1 Standard water area,length of 600 km,width of 192 km
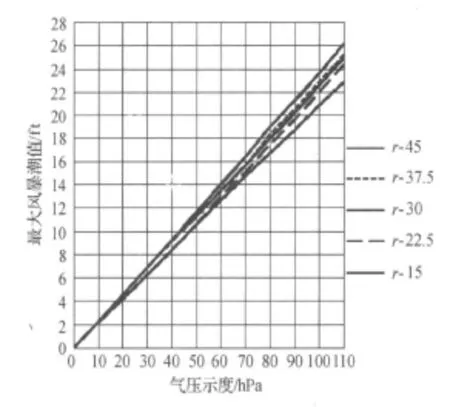
图2 最大增水诺模图Figure 2 Peak storm surge nomogram
第二张诺模图是对矢量风暴运动的修正因子图.除了气压示度和最大风速半径,矢量风暴运动,对风暴潮的成长也有很大的影响.这里主要考虑了运动方向和速度的影响.假定所有风暴都做标准运动,且所有台风中心气压示度和最大风速半径都保持不变[7,8],计算不同风暴移向和移速下的最大增水值,从而绘制出第二张诺模图,如图3.图中,θ表示风暴路径与海岸的交角,其确定方法如图3右上角小图:左边是陆地,右边是海,观测者在左边,以向北方向为零度基准,自海岸起顺时针转到风暴潮路径上即为θ值.
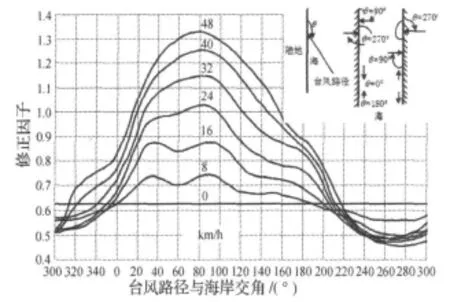
图3 矢量风暴运动修正因子诺模图Figure 3 Nomogram ofthevectorstorm movement's revising
第三张诺模图是修正海底地形的诺模图.不同的海底地形其水深和底摩擦因子不同,同样会对风暴潮产生一定的影响.假定所有风暴都做标准运动,且所有风暴R=36 km和 Δ P=62 hPa,表1给出了我国部分沿海验潮站的海底地形修正值,用FD表示.
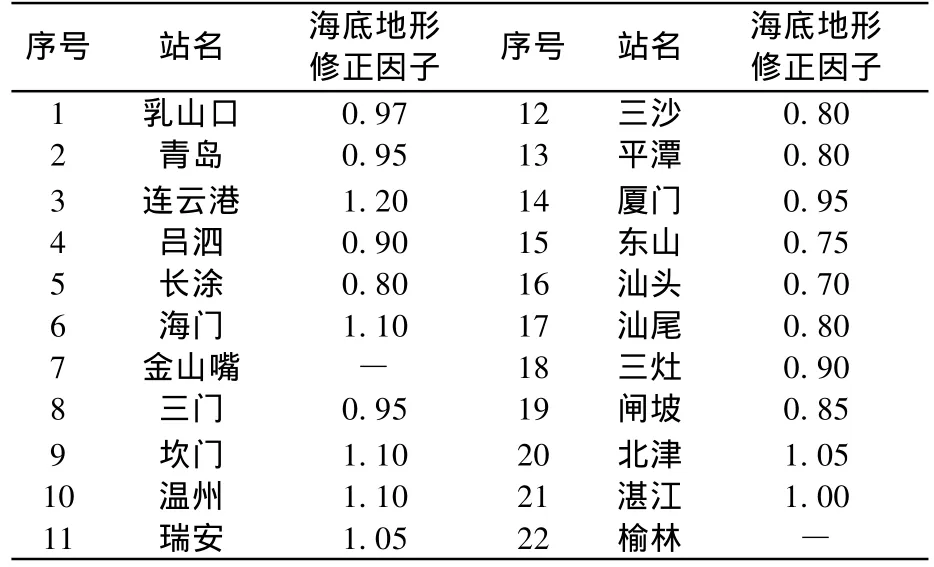
表1 我国沿海部分站的海底地形修正因子Table 1 Topography correction factor of the coastal part of the station in our country
计算一次风暴潮的最大增水时,首先确定海岸上的最大增水的位置,查出海底地形修正因子,再根据ΔP和R得到最大增水初估值,然后进入第二张诺模图,用风暴移速VS为参数,根据风暴路径与海岸的交角θ,查算出矢量风暴运动的修正因子FM的值.最后将SP、FD、FM连乘就获得了预报的最大增水值SS.
2 对SPLASH模式诺模图的修正与完善
2.1 对最大增水诺模图的修正
如图4,图中给出了五条气压示度和最大风速半径的函数曲线,从上到下依次为:R=30,R=37.5,R=22.5,R=45,R=15.根据文献[5]中最大增水诺模图推断,虽然最大风暴潮高度大小主要取决于ΔP值,最大风速半径对其仍有一定的影响,并且最大风速半径越大,最大风暴潮高度也越大,所以,SPLASH模式中五条气压示度和最大风速半径的函数曲线所对应的最大风速半径从上到下应该依次为R=45,R=37.5,R=30,R=22.5,R=15.通过后面算例的验证也同样证实了这一推断的正确性.
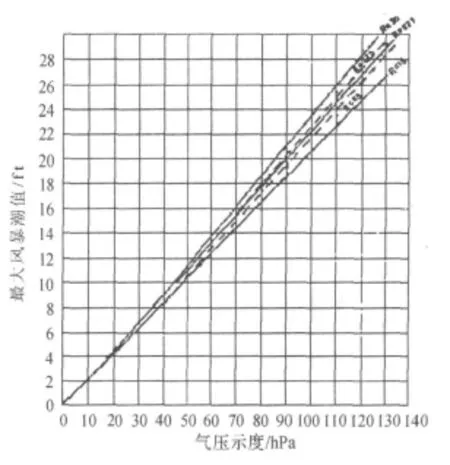
图4 最大增水诺模图原图[8]Figure 4 Peak storm surge nomogram
2.2 对矢量风暴运动订正因子诺模图的完善
如图5,下图中共有7条风暴路径相对海岸交角-修正因子曲线,分别为0 km/h,8 km/h,16 km/h,24 km/h,32 km/h,40 km/h,和48 km/h的情况.其中16 km/h,24 km/h,32 km/h,48 km/h的曲线都不完整,这样会增加编程计算的难度,并影响计算准确度.于是本文对该图进行了完善,将缺少的数据填补完整.主要从曲线的数值光滑性和总体趋势方面考虑,并且参考文献[5],利用曲线板的圆滑性将曲线自然延伸以填补缺少的曲线,为之后的插值计算做准备.当然,这种方法未必科学且必定会有一定误差,但是从实际情况考虑,一般风暴路径与海岸交角不超过180°,即范围在0~180°.由图5可以看出,在0~220°的θ范围,7条曲线的数据都十分完整,因而基本不会对结果产生太大影响.同时,即便在范围之外,经过插值计算之后也会减小修正因子的误差,从而使得到的最大增水值SS的误差在可接受范围内,所以这种数值处理方法仍然可以成立,并且方便有效.
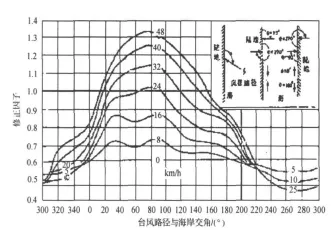
图5 矢量风暴运动订正因子诺模图原图[8]Figure 5 Nomogram of the vector storm movement's revising
3 SPLASH模式诺模图法预报实例
为了能够通过程序实现诺模图的查算,精确的计算方法是十分必要的.对两张诺模图进行分析,进而选用了二元插值算法[9-11],为了进一步保证精度,这里选用了二元三点插值和二元全区间插值算法分别计算,然后求其平均值,即可计算出插值点(u,v)处的函数近似值.最后将两种插值算法求出的值取平均即为所需要的最终结果.
本文中用到的诺模图数据来自王喜年先生的论文,本文中的两张诺模图(图2和图3)是根据论文[8]给出的诺模图而完成的,为了确保足够的精确度,对第一张诺模图(图2)每条曲线均匀的选取了12个点;对第二张诺模图(图3)均匀的选取了73个点,由图2与图4,图3与图5比较可以看到,这样的取法是成功的,可以高精度地还原原图.
将图2、图3所得数据分别进行插值计算,求出SP和FM,再由表1查出FD,然后根据公式SS=SP×FM×FD,即可得到最大风暴潮的增水值.
上述过程用VC++编程实现并调试通过,下面给出几个完整的算例来加以比较.
3.1 算例1
6903号台风作为台风历史上罕见的双台风,给广东省境内造成了极大的灾害.将该台风作为算例具有典型意义.
数据来自文献[8].如表2.

?
由于6903号台风数据稀少,无法将计算结果直接与验潮站观测的实际增水值相比较.从表3可以看出,本文计算结果与原文的误差在4%以内,预报结果较好.
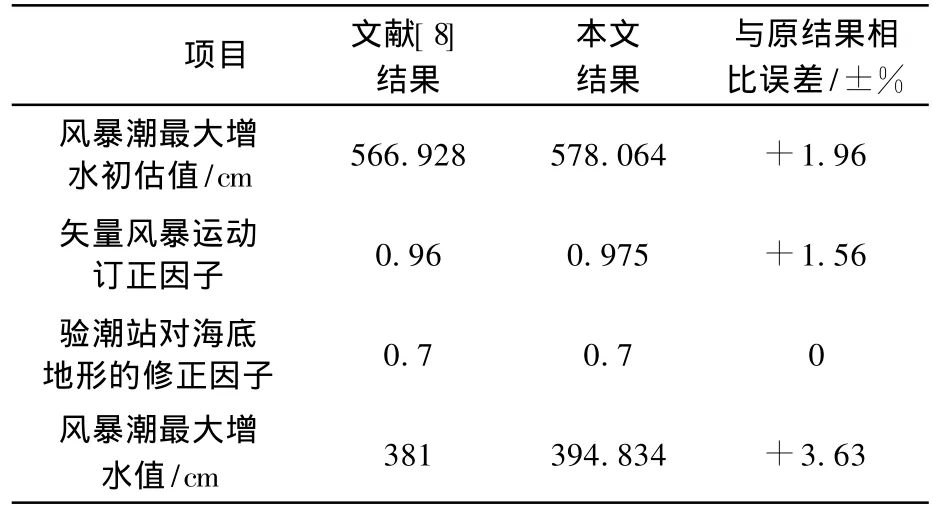
表3 计算结果Table 3 Calculation results
3.2 算例2
来自文献[8].如表4.

?
从表5可以看出,本文计算结果与原文的误差在3%以内,结果是可以信赖的.
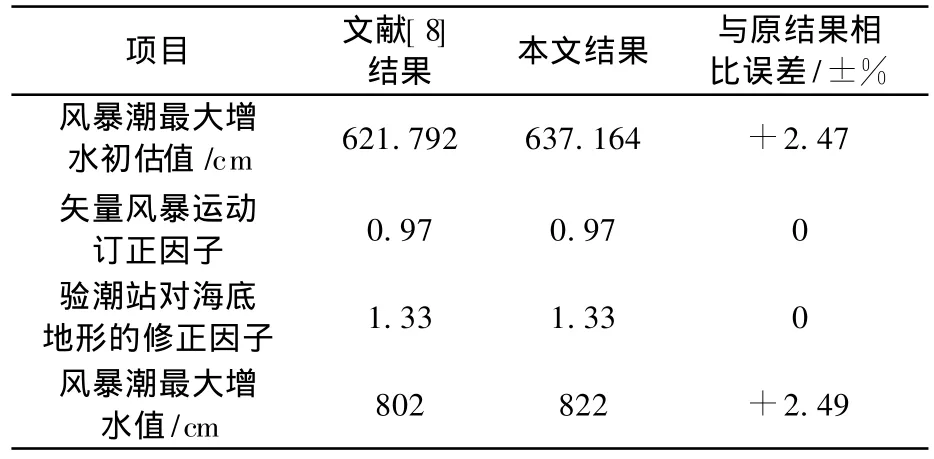
表5 计算结果Table 5 Calculation results
3.3 算例3
来自我国0608号台风“桑美”的数据.

表6 我国0608号台风预报最大增水计算数据Table 6 Data of peak storm surge about the Typhoon forecast of 0608 in our country

表7 计算结果Table 7 Calculation results
在“桑美”登陆时,温州有记录的过程最大增水是3.58 m,与本文计算结果相差35 cm,可以满足预报的基本要求.
4 结 语
本文介绍了SPLASH模式诺模图预报风暴潮最大增水的一般过程,并对SPLASH模式诺模图做了一定的修正和完善,使对其的编程计算更加易于实现且结果更精确.同时给出了3个算例加以验证.在今后的进一步的研究中,尚需要编制可视化数值预报程序,使得风暴潮的发展过程能在地图上动态显示[12],以提高程序的实用性.
[1]冯士筰.风暴潮导论[M].北京:科学出版社,1982:230-241.
[2]刘 宁.风暴潮灾害防治及海堤工程技术研讨会论文集[M].北京:中国水利水电出版社,2008:3-13.
[3]达 斯,宫崎正卫,捷列斯尼扬斯基.台风风暴潮预报技术手册[M].王喜年,译.北京:海洋出版社,1982:48-79.
[4]张火明,孙志林,苏中地.诺模图法预报风暴潮的高精度数值实现[J].中国计量学院学报,2009,20(1):59-64.
[5]王喜年.开阔海风暴潮的数值计算[J].海洋通报,1989,8(3):11-20.
[6]JAKOBSEN F,MADSEN H.Comparison and further development of parametric tropical cyclone models for storm surge modeling[J].Journal of Wind Engineering and Industrial Aerodynamics,2004,92:375-391.
[7]G RABER H C,CARDONE V J,JENSEN R E,et al.Coastal forecasts and storm surge predictions for tropical cyclones:A timely partnership program[J].Oceanography,2006,19(1):130-141.
[8]王喜年.SP LASH模式诺模图方法在我国的应用[J].海洋通报,1983,2(4):26-31.
[9]张火明,陆慧娟,卫 伟.混合离散变量模拟退火方法及其应用[J].中国计量学院学报,2006,17(1):44-49.
[10]高明正,金尚忠,张火明.改进的混合粒子群优化算法[J].中国计量学院学报,2008,19(3):260-264.
[11]徐士良.C常用算法程序集[M].3版.北京:清华大学出版社,1996:135-138.
[12]柏亚周,李训强,郑崇伟,等.风暴潮集合预报现状及前景展望[J].中国科技信息,2011,4:28-30.

