随机线元落入缓冲区内的概率分布函数研究
苗则朗,冯永兴,张书毕,张秋昭
(1.中国矿业大学环境与测绘学院,江苏徐州 221008;2.江苏省资源环境信息工程重点实验室,江苏徐州 221008)
随机线元落入缓冲区内的概率分布函数研究
苗则朗1,2,冯永兴1,张书毕1,张秋昭1
(1.中国矿业大学环境与测绘学院,江苏徐州 221008;2.江苏省资源环境信息工程重点实验室,江苏徐州 221008)
通过仿真计算出随机线元落入其“真实值”缓冲区内的比例,并采用柯氏检验法对其进行分布拟合检验,得出随机线元落入缓冲区内的比例服从正态分布的结论,从而完善线元误差不确定带模型。
随机线元;缓冲区;正态分布;柯氏检验法
一、引 言
线状地形物的特征一般包括长度和曲率,通常线状地形物的真实位置不容易获得或者获得的方式比较困难[1],因此不容易对线元整体精度作出评价。有关线状地形物精度评价目前已有多种模型。Perkal于 1956年首先提出了应用 Epsilon带模型来建立线元不确定性模型[2],围绕“真实”的位置建立宽度相等的缓冲区,比较测量值与“真值”之间的关系;Blakemore定义了点与线段的缓冲区之间的五种位置关系:绝对在、有可能在、模棱两可、可能不在、绝对不在[3];Skidmore和 Turner通过查找测量与参考线元之间的数目估计线元的精度[4];Goodchild和Hunter利用随机线元落入缓冲区内的比例评价随机线元的精度[5];Tveite、Langass和张永彬等通过缓冲区叠置分析,评价测量数据精度[6-7]。但以上方法均假设参考线元与测量线元之间不存在偏移,仅考虑方差的影响。为克服以上方法的不足,Joon Heo等在考虑偏移、方差的综合影响下,提出了非线性最小二乘方法[1],并将该方法应用于海岸线退化研究[8]。
以上模型与方法,均直接假设随机线元落入缓冲区内的比例服从高斯正态分布,但没有给出具体的原因或者推导过程,体系稍欠完善。本文基于计算机仿真和分布拟合检验的方法,采用柯尔莫戈罗夫(KolmogorovA N)检验法对假设的正态分布进行分布拟合检验,给出了随机线元落入缓冲区内的比例服从高斯正态分布的结论及证明过程。
二、误差函数及柯氏检验法
在数学中,误差函数 erf(x)(也称为高斯误差函数)是一个特殊的函数 (非初等函数),在概率、统计、材料科学和偏微分方程等领域广泛应用。erf(x)定义为

误差函数与标准正态分布累积函数 (记为Φ)基本相同,可以通过比例和旋转运算等同。即
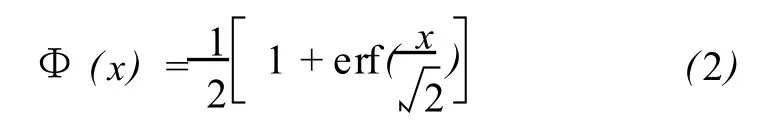
柯氏检验法由前苏联数学家柯尔莫戈罗夫首先提出,对于连续型的随机变量,柯氏检验法较χ2检验法更好。设 X的分布函数 F(x)是未知的;X1,…,Xn是样本;F0(x)是给定的某个分布函数;作如下假设

首先从样本出发求出经验分布函数 Fn(x),计算分歧度

取否定域为

当计算出分歧度 Dn的值小于临界值λ时,则接受 H0。临界值λ的取值可以由柯尔莫戈罗夫检验临界值表查知[9]。
三、模拟步骤及分布拟合分析
1.模拟步骤
随机线元及其使用“真实值”建立的缓冲区示意图如图 1所示,随机线元的分布受偏移和方差的影响,文献[1]论述了偏移和方差对随机线元分布的影响。综合考虑偏移和方差的影响,得出计算机仿真的步骤如下:
1)生成随机线元。模拟的点分别为 Z1、Z2,并假设 Z1、Z2相互独立。其分布依次为

利用Matlab生成上述两组随机点,连接两个随机点,即得到该线段一组随机线元。
2)围绕“真实”线段建立缓冲区。
3)计算随机线元落入缓冲区内的比例

4)采用蒙特卡罗方法重复以上三个步骤10 000次,将平均值作为该缓冲区带宽下随机线元落入带宽为缓冲区内的比例。
5)以一定的步长(如 0.5 m)增加缓冲区带宽,重复以上四个步骤,得到一系列不同缓冲区带宽下随机线元落入缓冲区内的比例。

图1 随机线元落入缓冲区示意图
2.模拟结果
随机线元落入缓冲区内的长度与随机线元长度的比值如表 1所示;随机线元落入缓冲区内的比例曲线图如图2所示。

表 1 随机线元落入缓冲区内的比例
从图 2中可以发现随机线元落入缓冲区内的比例曲线图与误差函数 erf(x)曲线图很接近,为了验证,采用柯氏检验法进行假设检验。

图 2 随机线元落入缓冲区内的比例
3.分布拟合检验
采用柯氏检验法进行假设检验。从图 2可以看出,该曲线的形态与正态分布的误差函数曲线相似,因此作如下假设

参数μ、σ的最大似然估计值

计算分歧度Dn

计算临界值λ

可知
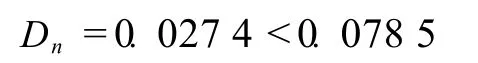
故认为 H0成立。因此,随机线元落入“真实值”缓冲区内的比例服从高斯正态分布的误差函数。
四、结果分析
本文通过计算机仿真,验证了随机线元落入缓冲区内的比例与正态分布有着密切的联系即其比例符合正态分布的误差函数,从体系上完善了 Epsilon带的应用。但文章不足之处在于:①模拟分析是在假设线元端点分布独立的情况下研究的,可以推广到误差相关的一般情形;②研究对象主要是线元,样本量较小,可以推广至折线、曲线等更加一般的情况,这是下一步工作的重点。
[1] JOON H,J IN W K,J I S P,et al.A New Line Accuracy Assess ment Methodology Using Nonlinear Least Squares Estimation[J].Journal of Surveying Engineering,2008, 134(1):13-20.
[2] PERKAL J.On Epsilon Length[J].Bulletin de l′Academic Polonaise des Sciences,1956(4):399-403.
[3] BLAK MORE M.Generalization and Error in Spatial Databases[J].Cartographica,1984,21(2-3):131-139.
[4] SK IDMORE A K,TURNER B J.Map Accuracy AssessmentUsingLine Intersect Sampling[J],Photogrammetric Engineering and Remote Sensing,1992,58(10): 1453-1457.
[5] GOODCH ILD M F,HUNTER G J.A Simple Positional AccuracyMeasure forLinear Features[J].International Journal on GeographicalInfor mation Science,1997, 11(3):299-306.
[6] TVEITE H,LANGASS S.An Accuracy Assess ment Method for Geographical Line Datasets Based on Buffering[J]. International Journal of Geographical Infor mation Science,1999,13(1):27-47.
[7] 张永彬,范爱民.基于误差熵不确定带的空间数据质量评价指标 [J].河北理工学院学报,2002(2): 121-127.
[8] JOON H,JUNG H K,J IN W K.A New Methodology for Measuring Coastline Recession Using Buffering and NonlinearLeast Squares Estimation[J]. International Journal of Geographical Information Science,2009,23(9): 1165-1177.
[9] 陈家鼎,孙山泽,李东风.数理统计学讲义[M].北京:高等教育出版社,2006:132-135.
Research on Probability D istribution Function of Random L ine within the Buffer Zone
M IAO Zelang,FENG Yongxing,ZHANG Shubi,ZHANGQiuzhao
0494-0911(2011)02-0029-02
P208
B
2010-05-07
苗则朗(1988—),男,安徽砀山人,博士生,主要研究方向为地理信息系统算法及遥感图像处理及模式识别。

