Delaunay三角网关键技术探讨

李小秋 ，许民献 ，尹志永

（1．桂林市测绘研究院，广西 桂林541002；2．河北省第三测绘院，河北 石家庄 050031；3．河北省基础地理信息中心，河北石家庄050031）

Delaunay三角网关键技术探讨

李小秋 ，许民献 ，尹志永

（1．桂林市测绘研究院，广西 桂林541002；2．河北省第三测绘院，河北 石家庄 050031；3．河北省基础地理信息中心，河北石家庄050031）

123

利用计算机技术，基于实际测量数据，利用逐点插入法，在不建立格网索引的情况下，提出一种高效的Delaunay三角网构建方法，与建立格网索引法搜索点所在的三角形相比，具有较高的执行效率。

Delaunay；不规则三角网；TIN；数据结构

由于Delaunay三角网具有最大的最小角及空外接圆两大重要性质，使剖分所得每个三角形最大限度地接近正三角形，因此它在所有的构网原则中是最优的，这使得它作为一种基本手段在地学分析、地理信息系统、虚拟现实以及道路设计等领域有着广泛的应用。

经过20多年的研究，国内外已经出现了不少成熟的Delaunay三角网生成算法，Lewis和Robinson提出了分治算法，Lawson提出了逐点插入法，Green和Sibson提出了三角网生长法；国内许多学者也在此基础上作了大量的研究，提出了卓有成效的改进算法。

三角网生长法由于算法复杂、时间效率差，在80年代中期以后的文献中已很少见，研究较多的是分治算法和逐点插入法。

分治算法构网速度快，其缺点是程序递归执行需要占用大量内存空间，数据预处理以及优化工作量大，对计算机硬件要求高；逐点插入法原理简单，占用内存资源少，编程容易实现，传统算法时间复杂度差，主要制约因素在于点在三角网中的查找和判断以及三角网的局部优化。文献［1］提出通过对原始数据预处理并进行格网化管理，从理论和实践均证明这是一种有效的提高逐点插入法构网速度的方法，已被广泛采用；但由于此方法需要对原始数据进行排序和对构网过程中的三角形进行格网管理，工作量较大，数据结构复杂，增加了编程的难度。笔者通过对逐点插入法深入剖析，提出了一种实用的方法，实践证明，其效率要优于格网化逐点插入法。

1 数据结构

三角网的数据存储方式比较复杂，它不仅要存储每个点的平面坐标及高程，还要存储边与点、边与三角形、点与三角形、以及三角形与三角形之间的拓扑关系；简洁而紧凑的数据结构不仅能优化内存使用，还能提高数据检索速度，它是提高构网效率的关键因素之一。以下是用C＋＋语言定义的三角网数据拓扑数据结构。

可以看出，以上数据结构除了点的三维坐标外，其余数据成员都是整型数，计算机对整型数的运算速度要大大快于对浮点数的运算速度；另外，在获得数据点的总数后要尽量一次性分配足够的内存空间，避免在程序运行过程中动态分配内存，造成内存使用碎片，降低构网速度。

2 数值运算

逐点插入算法是Lawson在1977年提出的，其基本思想是：对于一已经存在的三角形网络，当在其中插入一点时，将该点与包含它的三角形的三个顶点相连，从而与周围的三角形形成共用同一条对角线的四边形，然后逐个对四边形中的2个三角形进行空外接圆检测，如果不满足空外接圆准则，则用另一条对角线替换现有对角线；连续执行这一步骤，直到全部满足空外接圆准则为止［2］；基本过程如下：

1）遍历所有数据点，生成一矩形包容盒包含所有数据点，将此矩形包容盒分割为2个三角形。

2）数据点的逐点插入：从点集中顺次取出一点p，找到包含该点的三角形，P与包含三角形的顶点相连，形成3个新三角形，更新拓扑关系并将新生成的三角形加入优化队列中，如图1所示。

3）优化队列中的三角形。

4）重复2）、3），直到所有点插入完毕。

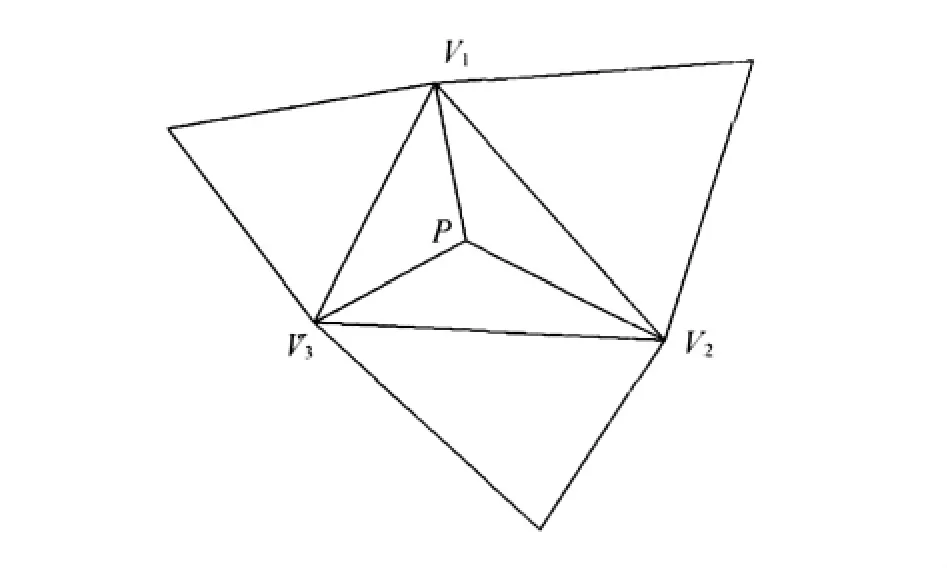
图1 在三角网中插入一点

可见，逐点插入法的时间主要耗费在定位三角形和三角网的优化上，随着点数的增加，三角形个数成倍增加，基于点在三角形中的查找判断过程是一个很费时的过程。

2．1 定位三角形

向初始三角网中添加构网点，就必须知道构网点所在的三角形，然后才可对初始三角网进行局部重构。如何快速找到构网点所在的三角形是逐点插入算法的核心问题。判断点是否在三角形内可以通过点与三角形三边的关系来判断；点与直线的关系可以用简化式（1）表示。

由上述关系可以知道点是否在三角形中；设构网点P与三角形三边的关系分别用d 1、d2、d3来表示，d1、d2、d3都是有向的并且按顺时针排列，如果三者都大于0，则点在三角形内部；如果两个大于0，另一个等于0，则点在三角形的一条边上；如果仅有一个大于0，另外两个等于0，则点与三角形的某顶点重合；否则点在三角形的外部。

遍历整个三角网，总可以找到点所在的三角形，当三角形个数较大时，这是个很费时的操作，消耗大量的时间，随着三角形个数的增多，构网速度会越来越低。

文献［1］通过对随机无序的散点和三角形建立格网索引来确定搜索起点三角形，使搜索起点三角形与目标三角形最近来减少搜索时间，这一方法与遍历整个三角网相比其搜索时间大幅度降低，但由于需要复杂的数据结构，消耗了大量的内存，使程序结构也相对复杂。

实际测量数据并非随机分布，而是局部基本有序的，笔者利用这一特性，将上一个插入三角形作为下一插入点的搜索起始三角形，不需要建立复杂的格网索引，只需要记录上一个目标三角形并作为下一插入点的搜索起始三角形，同样可以达到相同甚至较高的构网效率。

如图2所示，搜索起始三角形S确定后，使用方向搜索技术［3］可以迅速而精确地定位到插入点P所在的目标三角形T。

图2 方向搜索

2．2 三角网的优化

新点插入后，就可以根据优化条件来判断相邻三角形是否需要优化，优化条件为：公共边所对的2个内角和大于180°，可以证明仅此条件即可满足Delaunay三角网特征，如图3所示。

图3 三角网的优化

设：α1＝∠N1N3N2，α2＝∠N1N4N2．

显然，当（α1＋α2）＞180°时，也就是当满足条件sin（α1＋α2）＜0时，点 N4在三角形 N1N2N3的外接圆内，这时需要交换对角线。

本算法不需要对四点共圆和三点共线的情况进行特殊处理，并且其数值运算只有加、减和乘法，运算效率极高。

3 效率分析

图4为使用本文方法建立的某测区数字高程模型的一部分，计算机硬件配置为：P4 2．8 GHz 256 M内存。

图4 某测区局部构网样例

表1和图5为本文方法和格网索引法的效率分析，可以看出，点数和构网时间二者基本都为线性关系，而构网效率本文方法较高。

表1 构网效率对照表

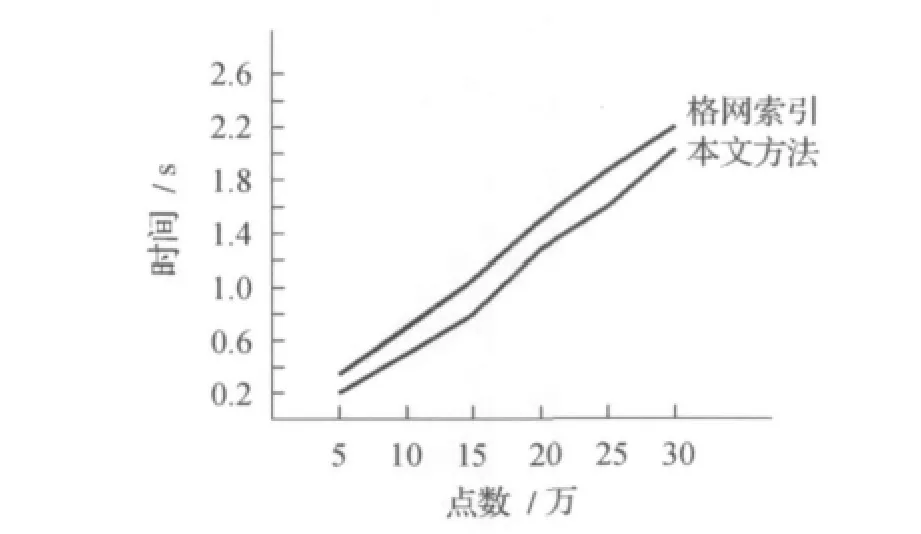
图5 效率对比

4 结束语

一个良好的数据结构和三角划分准则，必须由一个高效的算法和程序实现；算法在具体应用中发挥的作用由算法本身的性能和实现它的程序质量共同决定；逐点插入算法在解决了它的瓶颈问题后，其构网速度基本与分治算法接近。利用本文方法对实际测量数据构造Delaunay三角网的速度达到每秒15万个点，在效率上已经完全能满足工程设计的需要。

［1］蒋瑜，杜斌，卢军，等．基于Delaunay三角网的等值线绘制算法［J］．计算机应用研究，2010（1）：101－103．

［2］刘永和，王燕平，齐永安．一种快速生成平面Delaunay三角网的横向扩张法［J］．地球信息科学，2008，10（1）：20－25．

［3］胡金星，马照亭．基于格网划分的海量数据Delaunay三角剖分 ［J］．测绘学报，2004，33（2）：163－167．

［4］刘学军，符锌砂．公路数字地面模型整体建立原理及方法 ［J］．中国公路学报，2000，20（3）：16－20．

［5］刘少华，程朋根．Delaunay三角网内插特征点算法研究［J］．华东地质学院学报，2002，25（3）：254－257．

［6］方勇，刘鹏，胡海彦．一种Delaunay三角网的快速生成算法［J］．测绘科学与工程，2006，26（3）：1－4．

［7］周晓云，刘慎权．实现约束Delaunay三角剖分的健壮算法［J］．计算机学报，1996，19（8）：615－624．

Discussion on key technology of the Delaunay triangulated network

LI Xiao－qiu1，XU Min－xian2，YIN Zhi－yong3
（1．Guilin Institute of Surveying and Mapping，Guilin 541002，China；2．Hebei the Third Bureau of Surveying and Mapping，Shijiazhuang 050031，China；3．Hebei Geomatics Center，Shijiazhuang 050031，China）

A new efficient Delaunay triangulated network construction method is introduced using incremental inserting method based on real survey data without setting up grid index．Comparing with grid index method to find the triangle with the searching points located，this method has much higher executing efficiency．

Delaunay；irregular triangle network；TIN；data structure

P208

A

1006－7949（2011）06－0061－03

2011－09－28

李小秋（1974－），男，工程师．

［责任编辑张德福］